云南省临沧市耿马县2023年中考一模数学试卷

试卷更新日期：2023-05-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 某水库4月份的最高水位超过标准水位 $5 cm$ ，记为 $+ 5 cm$ ，最低水位低于标准水位 $3 cm$ ，记为 $- 3 cm$ ，则4月份该水库的水位差是（）

A、 $8 cm$ B、 $3 cm$ C、 $5 cm$ D、 $- 8 cm$

查看试题解析
2. 如图，已知直线a，b被直线c所截，若 $a ∥ b$ ， $∠ 1 = 69 °$ ，则 $∠ 2$ 的度数为（）

A、 $59 °$ B、 $111 °$ C、 $21 °$ D、 $69 °$

查看试题解析
3. 据悉，截至 $2022$ 年底，中国高铁营运里程约为 $420000$ 米，数据 $420000$ 用科学记数法可表示为（）

A、 $4.2 \times 10^{5}$ B、 $4.2 \times 10^{6}$ C、 $4.2 \times 10^{7}$ D、 $4.2 \times 10^{8}$

查看试题解析
4. 已知一个多边形的内角和为1080°，则这个多边形是（）

A、九边形 B、八边形 C、七边形 D、六边形

查看试题解析
5. 某校组织了以“我爱我的国”为主题的演讲比赛，如表是小智同学的得分情况，则他得分的平均数是（）

评委1

评委2

评委3

评委4

评委5

$9.8$

$9.7$

$9.6$

$9.5$

$9.4$

A、 $9.7$ B、 $9.6$ C、 $9.5$ D、 $9.65$

查看试题解析
6. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、平行四边形 B、矩形 C、直角三角形 D、角

查看试题解析
7. 按一定规律排列的单项式： $2 a^{2} ， 4 a^{3} ， 6 a^{4} ， 8 a^{5} ， 10 a^{6}$ ， ……，第n个单项式是（）

A、 $2 n a^{2 n}$ B、 $2 n a^{n}^{+ 1}$ C、 $n^{2} a^{n}^{+ 1}$ D、 $n^{2} a^{2 n}$

查看试题解析
8. 已知某几何体的三视图如图所示，则该几何体是（）

A、三棱柱 B、长方体 C、三棱锥 D、圆锥

查看试题解析
9. 反比例函数 $y = \frac{k}{x}$ 的图像如图所示，点A是其图像上的一点， $A B ⊥ x$ 轴，已知 $△ A O B$ 的面积为6，则k的值为（）

A、 $- 6$ B、6 C、 $- 12$ D、12

查看试题解析
10. 下列运算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 ${(a b^{3})}^{2} = a^{2} b^{5}$ C、 ${(2 a - b)}^{2} = 4 a^{2} - 2 a b + b^{2}$ D、 $\sqrt{{(- a)}^{2}} = | a |$

查看试题解析
11. 小科同学将一张直径为16的圆形卡纸平均分成4份，用其中一份作一个圆锥的侧面，则这个圆锥的底面半径是（）

A、2 B、4 C、8 D、16

查看试题解析
12. 某班为筹备迎新晚会，班长用420元到甲商店购买A材料，学习委员用300元到乙商店购买B材料，两人买回的A、B两种材料的数量一样多．已知A材料的单价比B材料贵2元，求B材料的单价是多少元？若设B材料的单价为x元，则可列方程为（）

A、 $\frac{420}{x + 2} = \frac{300}{x}$ B、 $\frac{420}{x - 2}$ $=$ $\frac{300}{x}$ C、 $\frac{420}{x}$ $=$ $\frac{300}{x + 2}$ D、 $\frac{420}{x} = \frac{300}{x - 2}$

查看试题解析

二、填空题

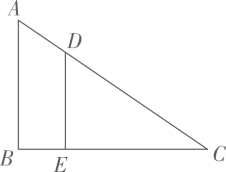
13. 函数y= $\sqrt{x + 2}$ 中，自变量x的取值范围是．

查看试题解析
14. 如图，在O ABC中，DE//AB，BE= 2，CE= 6，AD= 2.5，则AC的长为

查看试题解析
15. 分解因式：x²-6x+9=.

查看试题解析
16. 已知 $A B = 12$ ， C、D是以 $A B$ 为直径的 $⊙ O$ 上的任意两点，连接 $C D$ ，且 $A B ⊥ C D$ ，垂足为M， $∠ O C D = 30 °$ ，则线段 $M B$ 的长为．

查看试题解析

三、解答题

17. 计算： $\frac{3}{4} \times (- 12) + 2 \sin 45 ° - {(\sqrt{2} - 1)}^{0} + {(\frac{1}{3})}^{- 2}$ ．

查看试题解析
18. 如图，已知 $∠ B = ∠ D ， B C = D C$ ，求证： $A B = E D$ ．

查看试题解析

19. 某学校为了增强学生对数学课程的兴趣，开设了五期“走进古典数学著作”的系列专题讲座，分别讲解了《周髀算经》（A期）、《九章算术》（B期）、《数书九章》（C期）、《孙子算经》（D期）和《海岛算经》（E期）等五部中国古典数学著作，学校为了解学生对本次系列讲座的喜爱情况，随机抽取了本校部分学生进行调查（每名学生选择并且只能选择一期喜爱的讲座），现将收集的数据整理成如下统计表和扇形统计图．

讲座代号	A	B	C	D	E	合计
学生人数	a	b	11	9	12	50

(1)、求出a、b的值．

(2)、在扇形统计图中，C所在扇形的圆心角为

m °

，求m的值．

(3)、若该校有1500名学生，请你估计该校喜欢E期（《海岛算经》）讲座的学生人数．

查看试题解析

20. 某社区组织100名志愿者参加3项公益活动，分别是“A：清理社区绿化带垃圾”、“B：社区敬老院服务”、“C：公益知识宣讲”，每人任选一项参加即可．小明和小刚两位同学也参加了这次活动．

(1)、小明选择参加公益知识宣讲的概率是．

(2)、用列表或画树状图的方法求小明和小刚至少有一人参加社区敬老院服务的概率．

查看试题解析
21. 如图，在 $Rt △ A B C$ 中， $∠ A B C = 90 °$ ， $D$ 、 $E$ 分别为 $A C$ 、 $B C$ 的中点，连接 $D E$ 并延长 $D E$ 至点 $F$ ，且 $D E = E F$ ，点 $P$ 为直线 $B C$ 上的一个动点．

(1)、求证：四边形 $B F C D$ 为菱形．

(2)、若 $A B = 6$ ，菱形 $B F C D$ 的面积为24，求 $D P + A P$ 的最小值．

查看试题解析
22. 为全面推进乡村振兴，某省实行城市援助乡镇的政策．该省的A市有120吨物资，B市有130吨物资．经过调研发现该省的甲乡需要140吨物资，乙乡需要110吨物资．于是决定由A、B两市负责援助甲、乙两乡、已知从A市往甲、乙两乡运送物资的运费分别为300元/吨、150元/吨，从B市往甲、乙两乡运送物资的运费分别为200元/吨、100元/吨．

(1)、设从A市往甲乡运送x吨物资，从A、B两市向甲、乙两乡运送物资的总运费为y元，求y与x的函数解析式．

(2)、请设计运费最低的运送方案，并求出最低运费．

查看试题解析
23. 如图，在 $△ A B C$ 中， $A B = A C$ ，点O在 $A B$ 上，以 $O B$ 为半径的 $⊙ O$ 分别与 $B C$ 、 $A B$ 相交于点D、F，与 $A C$ 相切于点E，过点D作 $D G ⊥ A C$ ，垂足为G．

(1)、求证： $D G$ 是 $⊙ O$ 的切线．

(2)、若 $C G = 2 ， C D = 8$ ，求 $B D$ 的长．

查看试题解析
24. 在平面直角坐标系中，抛物线 $y = a x^{2} + b x - 6 (a \neq 0)$ 与 $x$ 轴交于点 $A (- 3 ， 0)$ 和点 $B (1 ， 0)$ ，与 $y$ 轴交于点 $C$ ，点 $D$ 在抛物线的对称轴上．

(1)、若点E在x轴下方的抛物线上，求 $△ A B E$ 面积的最大值．

(2)、抛物线上是否存在一点F，使得以点A，C，D，F为顶点的四边形为平行四边形？若存在，求出点F的坐标，若不存在，请说明理由．

查看试题解析

评委1	评委2	评委3	评委4	评委5
$9.8$	$9.7$	$9.6$	$9.5$	$9.4$