云南省昆明市安宁市2023年中考一模数学试卷
试卷更新日期:2023-05-25 类型:中考模拟
一、单选题
-
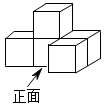
1. 中国是最早采用正负数表示相反意义的量,并使用负数进行运算的国家.当前,手机移动支付已经成为新型的消费方式,节日当天妈妈收到微信红包80元记作元,则妈妈微信转账支付67元可以表示为( )A、元 B、元 C、元 D、元2. 根据有关部门测算,年春节假期期间,云南省共接待游客的数量大约为人次.数据用科学记数法表示为( )A、 B、 C、 D、3. 如图是由5个完全相同的小正方体摆成的几何体,则这个几何体的主视图是( )
 A、
A、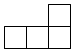 B、
B、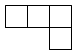 C、
C、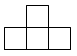 D、
D、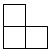 4. 如图,直线 , 若 , 则为( )
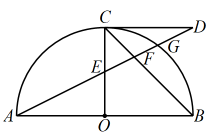
4. 如图,直线 , 若 , 则为( )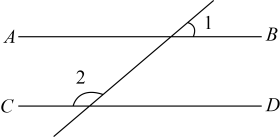 A、 B、 C、 D、5. 已知点A(1,-3)关于x轴的对称点在反比例函数的图像上,则实数k的值为( )A、3 B、 C、-3 D、6. 一个多边形的内角和等于外角和的2倍,这个多边形是( )A、六边形 B、七边形 C、八边形 D、十边形7. 下列运算正确的是( )A、 B、 C、 D、8. 如图,是的外接圆,是的直径,点在上,若的半径为6, , 则的长度为( )
A、 B、 C、 D、5. 已知点A(1,-3)关于x轴的对称点在反比例函数的图像上,则实数k的值为( )A、3 B、 C、-3 D、6. 一个多边形的内角和等于外角和的2倍,这个多边形是( )A、六边形 B、七边形 C、八边形 D、十边形7. 下列运算正确的是( )A、 B、 C、 D、8. 如图,是的外接圆,是的直径,点在上,若的半径为6, , 则的长度为( )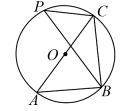 A、3 B、 C、 D、69. 按一定顺序排列的单项式: , , , , , , ……,第n个单项式是( )A、 B、 C、 D、10. 随着初中学业水平考试的临近,某校连续四个月开展了学科知识模拟测试,并将测试成绩整理,绘制了如图所示的统计图(四次参加模拟考试的学生人数不变),下列四个结论不正确的是( )
A、3 B、 C、 D、69. 按一定顺序排列的单项式: , , , , , , ……,第n个单项式是( )A、 B、 C、 D、10. 随着初中学业水平考试的临近,某校连续四个月开展了学科知识模拟测试,并将测试成绩整理,绘制了如图所示的统计图(四次参加模拟考试的学生人数不变),下列四个结论不正确的是( )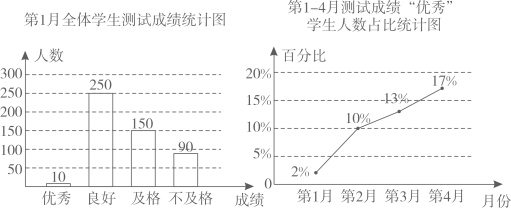 A、共有500名学生参加模拟测试 B、从第1月到第4月,测试成绩“优秀”的学生人数在总人数中的占比逐渐增长 C、第4月增长的“优秀”人数比第3月增长的“优秀”人数多 D、第4月测试成绩“优秀”的学生人数达到100人11. 如图,在△ABC中两条中线BE、CD相交于点O,记△DOE的面积为S1 , △COB的面积为S2 , 则S1:S2=( )
A、共有500名学生参加模拟测试 B、从第1月到第4月,测试成绩“优秀”的学生人数在总人数中的占比逐渐增长 C、第4月增长的“优秀”人数比第3月增长的“优秀”人数多 D、第4月测试成绩“优秀”的学生人数达到100人11. 如图,在△ABC中两条中线BE、CD相交于点O,记△DOE的面积为S1 , △COB的面积为S2 , 则S1:S2=( )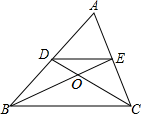 A、1:4 B、2:3 C、1:3 D、1:212. “爱劳动,劳动美.”甲、乙两同学同时从家里出发,分别到距家6km和10km的实践基地参加劳动.若甲、乙的速度比是 ,结果甲比乙提前20min到达基地,求甲、乙的速度.设甲的速度为3xkm/h,则依题意可列方程为( )A、 B、 C、 D、
A、1:4 B、2:3 C、1:3 D、1:212. “爱劳动,劳动美.”甲、乙两同学同时从家里出发,分别到距家6km和10km的实践基地参加劳动.若甲、乙的速度比是 ,结果甲比乙提前20min到达基地,求甲、乙的速度.设甲的速度为3xkm/h,则依题意可列方程为( )A、 B、 C、 D、二、填空题
-
13. 若二次根式 有意义,则实数x的取值范围是 .14. 如图,以△ABC的顶点B为圆心,BA长为半径画弧,交于点 , 连接AD.若∠B=40°,∠C=36°,则∠DAC的大小为度.
 15. 分解因式: .16. 如图,边长为2的正方形ABCD的对角线AC、BD相交于点O,若以C为圆心,CO的长为半径画圆,则图中阴影部分的面积是 .
15. 分解因式: .16. 如图,边长为2的正方形ABCD的对角线AC、BD相交于点O,若以C为圆心,CO的长为半径画圆,则图中阴影部分的面积是 .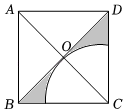
三、解答题
-
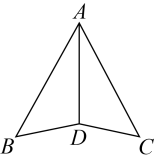
17. 计算:18. 如图,已知平分 , . 求证: .
 19. 为了加强对青少年防溺水安全教育,4月初某校开展了“远离溺水,珍爱生命”的防溺水安全知识比赛.下面是从参赛学生中随机收集到的20名学生的成绩(单位:分):
19. 为了加强对青少年防溺水安全教育,4月初某校开展了“远离溺水,珍爱生命”的防溺水安全知识比赛.下面是从参赛学生中随机收集到的20名学生的成绩(单位:分):87 99 86 89 91 91 95 96 87 97
91 97 96 86 96 89 100 91 99 97
整理数据:
成绩(分)
86
87
89
91
95
96
97
99
100
学生人数(人)
2
2
2
4
1
3
3
2
1
分析数据:
平均数
众数
中位数
93
a
b
解决问题:
(1)、直接写出:上面表格中的 , ;(2)、若成绩达到95分及以上为“优秀”等级,求“优秀”等级所占的百分率为;(3)、请估计该校1500名学生中成绩达到95分及以上的学生人数.20. 在一个不透明的袋子中装有完全相同的四个小球,小球上分别标有数字 , , 0,4,现从中任意摸出一个小球,将小球上面的数字记为a;将球放回袋中搅匀,再从中任意摸出一个小球,将小球上面的数字记为b.(1)、从袋子中随机摸出一个小球,摸到的数字是有理数属于事件(填“不可能”、“必然”或者“随机”);(2)、用列表或画树状图的方法表示出所有可能出现的结果,并求出点在第四象限的概率.21. 如图,在中, , 于D, , , 连接交于点O.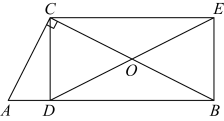 (1)、求证:四边形是矩形;(2)、如果 , , 求的长.22. 黔东南州某超市购进甲、乙两种商品,已知购进3件甲商品和2件乙商品,需60元;购进2件甲商品和3件乙商品,需65元.(1)、甲、乙两种商品的进货单价分别是多少?(2)、设甲商品的销售单价为x(单位:元/件),在销售过程中发现:当11≤x≤19时,甲商品的日销售量y(单位:件)与销售单价x之间存在一次函数关系,x、y之间的部分数值对应关系如表:
(1)、求证:四边形是矩形;(2)、如果 , , 求的长.22. 黔东南州某超市购进甲、乙两种商品,已知购进3件甲商品和2件乙商品,需60元;购进2件甲商品和3件乙商品,需65元.(1)、甲、乙两种商品的进货单价分别是多少?(2)、设甲商品的销售单价为x(单位:元/件),在销售过程中发现:当11≤x≤19时,甲商品的日销售量y(单位:件)与销售单价x之间存在一次函数关系,x、y之间的部分数值对应关系如表:销售单价x(元/件)
11
19
日销售量y(件)
18
2
请写出当11≤x≤19时,y与x之间的函数关系式.
(3)、在(2)的条件下,设甲商品的日销售利润为w元,当甲商品的销售单价x(元/件)定为多少时,日销售利润最大?最大利润是多少?