上海市徐汇区2023年中考二模数学试卷

试卷更新日期：2023-05-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列互为倒数的是（）

A、 $3$ 和 $\frac{1}{3}$ B、 $- 2$ 和 $2$ C、 $3$ 和 $- \frac{1}{3}$ D、 $- 2$ 和 $\frac{1}{2}$

查看试题解析
2. 下列运算结果错误的是（）

A、 $m^{2} \div m^{3} = m^{- 1}$ B、 ${(m^{2})}^{3} = m^{6}$ C、 $m^{2} \cdot m^{3} = m^{5}$ D、 $m^{2} + m^{3} = m^{5}$

查看试题解析
3. 如图，数轴上的点A和点B分别在原点的左侧和右侧，点A、B对应的实数分别是a、b，下列结论一定成立的是（）

A、 $a + b < 0$ B、 $b - a < 0$ C、 $- 2 a > - 2 b$ D、 $| a | > | b |$

查看试题解析
4. 如果点 $(- 2 ， y_{1})$ 、 $(- 1 ， y_{2})$ 、 $(2 ， y_{3})$ 在反比例函数 $y = \frac{k}{x} (k < 0)$ 的图象上，那么（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{2} > y_{1} > y_{3}$ C、 $y_{3} > y_{1} > y_{2}$ D、 $y_{3} > y_{2} > y_{1}$

查看试题解析

5. 某校足球社团有50名成员，下表是社团成员的年龄分布统计表，对于不同的m（m为0~14的整数），下列关于年龄的统计量不会发生改变的是（）

年龄（单位：岁）	13	14	15	16	17
频数（单位：名）	12	15	m	$14 - m$	9

A、平均数、中位数 B、平均数、方差 C、众数、中位数 D、众数、方差

查看试题解析

6. 如图，在梯形 $A B C D$ 中，已知 $A D ∥ B C$ ， $A D = 3$ ， $B C = 9$ ， $A B = 6$ ， $C D = 4$ ，分别以 $A B$ 、 $C D$ 为直径作圆，这两圆的位置关系是（）

A、内切 B、外切 C、相交 D、外离

查看试题解析

二、填空题

7. 计算： $4^{\frac{1}{2}}$ ＝.

查看试题解析
8. 已知f（x）＝ $\frac{2}{x - 1}$ ，则 $f (\sqrt{3})$ ＝．

查看试题解析
9. 根据电影发行方的数据，电影《满江红》截至2023年3月17日，以4535000000元的票房高居春节档前列，数据4535000000用科学记数法表示为．

查看试题解析
10. 方程组 ${\begin{array}{l} x^{2} - 3 x y + 2 y^{2} = 0 \\ x + y = 3 \end{array}$ 的解是．

查看试题解析
11. 妈妈煮了4个汤圆，分别是2个花生味和2个芝麻味，小明随意吃两个恰好都是花生味的概率是．

查看试题解析
12. 关于x的方程 $x^{2} - 2 x - m = 0$ 有两个不相等的实数根，则m的取值范围是．

查看试题解析
13. 如图，已知在 $△ A B C$ 中，点D是边AC上一点，且 $C D = 2 A D$ ．设 $\vec{B A} = \vec{a}$ ， $\vec{B C} = \vec{b}$ ，那么向量 $\vec{B D} =$ ．（用 $x \vec{a} + y \vec{b}$ 的形式表示，其中x、y为实数）

查看试题解析
14. 为了了解学生在家做家务情况，某校对部分学生进行抽样调查，并绘制了如图所示的频数分布直方图（每组数据含最小值，不含最大值）．如果该校有1500名学生，估计该校平均每周做家务的时间少于2小时的学生人数约是人．

查看试题解析
15. 某公司产品的销售收入 $y_{1}$ 元与销售量x吨的函数关系记为 $y_{1} = f (x)$ ，销售成本 $y_{2}$ 与销售量x的函数关系记为 $y_{2} = g (x)$ ，两个函数的图象如图所示．当销售收入与销售成本相等时，销售量x为吨．

查看试题解析
16. 如图，已知 $⊙ O$ 的内接正方形 $A B C D$ ，点 $F$ 是 $\overset{⌢}{C D}$ 的中点， $A F$ 与边 $D C$ 交于点 $E$ ，那么 $\frac{E F}{A E} =$ ．

查看试题解析
17. 如图，抛物线 $C_{1}$ ： $y = x^{2} + 2 x - 3$ 与抛物线 $C_{2}$ ： $y = a x^{2} + b x + c$ 组成一个开口向上的“月牙线”，抛物线 $C_{1}$ 和抛物线 $C_{2}$ 与x轴有着相同的交点A、B（点B在点A右侧），与y轴的交点分别为C、D．如果 $B D = C D$ ，那么抛物线 $C_{2}$ 的表达式是．

查看试题解析
18. 如图，在直角坐标系中，已知点 $A (8 ， 0)$ 、点 $B (0 ， 6)$ ， $⊙ A$ 的半径为5，点C是 $⊙ A$ 上的动点，点P是线段 $B C$ 的中点，那么 $O P$ 长的取值范围是．

查看试题解析

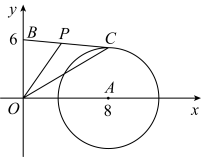
三、解答题

19. 先化简： $(\frac{1}{x + 3} - 1) \div \frac{x^{2} - 4}{x^{2} + 6 x + 9}$ ，然后从 $- 3$ 、 $- 2$ 、0、2、3中选一个数代入求值．

查看试题解析
20. 解不等式组： ${\begin{matrix} 3 x + 6 \geq 5 (x - 2) \\ 1 - \frac{x - 2}{3} \leq \frac{2 x - 1}{2} \end{matrix}$

查看试题解析
21. 如图， $A D 、 A E$ 分别是 $△ A B C$ 边 $B C$ 上的高和中线，已知 $B C = 8$ ， $\tan B = \frac{1}{3}$ ， $∠ C = 45 °$ ．

(1)、求 $A D$ 的长；

(2)、求 $\sin ∠ B A E$ 的值．

查看试题解析
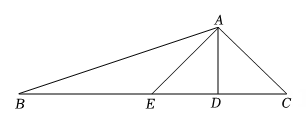22. 小明家的花洒的实景图及其侧面示意图分别如图1、图2所示，花洒安装在离地面高度 $160$ 厘米的A处，花洒 $A D$ 的长度为 $20$ 厘米．

(1)、已知花洒与墙面所成的角 $∠ B A D = 120 °$ ，求当花洒喷射出的水流 $C D$ 与花洒 $A D$ 成 $90 °$ 的角时，水流喷射到地面的位置点C与墙面的距离．（结果保留根号）

(2)、某店铺代理销售这种花洒，上个月的销售额为 $2400$ 元，这个月由于店铺举行促销活动，每个花洒的价格比上个月便宜 $2$ 0元，因此比上个月多卖出8个的同时销售额也上涨了 $400$ 元，求这个此款花洒的原价是多少元？

查看试题解析
23. 如图，已知 $⊙ O$ 是 $△ A B C$ 的外接圆，连接 $A O$ 并延长交边 $B C$ 于点D，连接 $O C$ ，且 $D C^{2} = O D \cdot A D$ ．

(1)、求证： $A C = B C$ ；

(2)、当 $A B = A D$ 时，过点A作边 $B C$ 的平行线，交 $⊙ O$ 于点E，连接 $O E$ 交 $A C$ 于点F．请画出相应的图形，并证明： $A D \cdot A E = B C \cdot E F$ ．

查看试题解析
24. 如图，已知抛物线 $y = x^{2} + b x + c$ 经过点 $A (- 2 ， 7)$ ，与x轴交于点B、 $C (5 ， 0)$ ．

(1)、求抛物线的顶点M的坐标；

(2)、点E在抛物线的对称轴上，且位于x轴的上方，将 $△ B C E$ 沿直线BE翻折，如果点C的对应点F恰好落在抛物线的对称轴上，求点E的坐标；

(3)、点P在抛物线的对称轴上，点Q是抛物线上位于第四象限内的点，当 $△ C P Q$ 为等边三角形时，求直线 $B Q$ 的表达式．

查看试题解析
25. 已知：如图1，四边形ABCD中， $A B = A D = C D$ ， $∠ B = ∠ C < 90 °$ ．

(1)、求证：四边形ABCD是等腰梯形；

(2)、边CD的垂直平分线EF交CD于点E，交对角线AC于点P，交射线AB于点F．
①当 $A F = A P$ 时，设AD长为x，试用x表示AC的长；

②当 $B F = D E$ 时，求 $\frac{A D}{B C}$ 的值．

查看试题解析