上海市浦东新区2023年中考二模数学卷
试卷更新日期:2023-05-25 类型:中考模拟
一、单选题
-
1. 下列分数中,能化成有限小数的是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 一元二次方程的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根4. 已知某校九年级200名学生义卖所得金额分布直方图如图所示,那么元这个小组的组频率是( )
 A、 B、 C、 D、5. 如图,已知正方形的顶点D、E在的边上,点G、F分别在边上,如果 , 的面积是32,那么这个正方形的边长是( )
A、 B、 C、 D、5. 如图,已知正方形的顶点D、E在的边上,点G、F分别在边上,如果 , 的面积是32,那么这个正方形的边长是( ) A、4 B、8 C、 D、6. 顺次联结四边形各边中点所得的四边形是矩形,那么四边形一定是( )A、菱形 B、对角线相等的四边形 C、对角线互相垂直的四边形 D、对角线互相垂直且平分的四边形
A、4 B、8 C、 D、6. 顺次联结四边形各边中点所得的四边形是矩形,那么四边形一定是( )A、菱形 B、对角线相等的四边形 C、对角线互相垂直的四边形 D、对角线互相垂直且平分的四边形二、填空题
-
7. 计算 .8. 分解因式: .9. 方程 的解是 .10. 不等式组的解集是 .11. 点在反比例函数的图象上,则k的值是 .12. 抛物线在y轴的左侧部分,y的值随着x的值增大而 . (填“增大”或“减小”)13. 不透明的布袋里有3个黄球、2个红球、5个白球,它们除颜色外其他都相同,那么从布袋中任意摸出一球恰好为红球的概率是 .14. 某企业今年第一季度各月份产值占这个季度总产值的百分比如图所示,已知二月份产值是36万元,那么该企业第一季度月产值的平均数是万元.
 15. 如果两圆的半径分别为5或2,圆心距为7,那么这两个圆的位置关系是 .16. 如图,过的重心G,设向量 , 那么向量(结果用、表示)
15. 如果两圆的半径分别为5或2,圆心距为7,那么这两个圆的位置关系是 .16. 如图,过的重心G,设向量 , 那么向量(结果用、表示)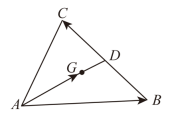 17. 如图,将矩形纸片沿对角线折叠,点B落在点E处,与边相交于点F.如果 , 那么的正弦值等于 .
17. 如图,将矩形纸片沿对角线折叠,点B落在点E处,与边相交于点F.如果 , 那么的正弦值等于 . 18. 我们规定:两个正多边形的中心之间的距离叫做中心距,在同一个平面内有边长都为6的正三角形和正方形,当它们的一边重合时,中心距为 .
18. 我们规定:两个正多边形的中心之间的距离叫做中心距,在同一个平面内有边长都为6的正三角形和正方形,当它们的一边重合时,中心距为 .三、解答题
-
19. 计算: .20. 解方程:21. 已知:如图,是的外接圆,平分的外角 , , , 垂足分别是点M,N,且 .
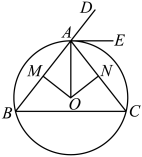 (1)、求的度数;(2)、如果 , , 求的半径长.22. 某市全面实施居民“阶梯水价”.当累计水量超过年度阶梯水量分档基数临界点后,即开始实施阶梯价格计价,分档水量和单价见下表:
(1)、求的度数;(2)、如果 , , 求的半径长.22. 某市全面实施居民“阶梯水价”.当累计水量超过年度阶梯水量分档基数临界点后,即开始实施阶梯价格计价,分档水量和单价见下表:分档
户年用水量(立方米)
自来水单价(元/立方米)
污水处理单价(元/立方米)
第一阶梯
0~220(含220)
2.25
1.8
第二阶梯
220~300(含300)
4
第三阶梯
300以上
6.99
注:应缴的水费=户年用水量×(自来水单价+污水处理单价)

仔细阅读上述材料,请解答下面的问题:
(1)、如果小叶家全年用水量是220立方米,那么她家全年应缴纳水费多少元?(2)、居民应缴纳水费y(元)关于户年用水量x(立方米)的函数关系如图所示,求第二阶梯(线段)的表达式;(3)、如果小明家全年缴纳的水费共计1181元,那么他家全年用水量是多少立方米?23. 已知:如图,在梯形中, , 过点B作 , 垂足为点E,点G在边上,连接、 , 对角线与、分别交于点F、H,且 .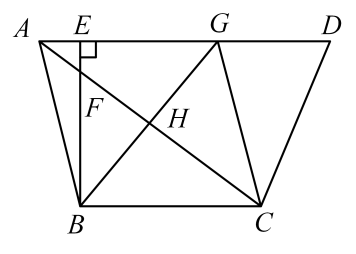 (1)、求证:;(2)、如果 , 且是与的比例中项,求证:四边形是菱形.24. 如图,直线与x轴交于点A,与y轴交于点C,抛物线经过A、C两点,且与x轴的另一个交点为B,抛物线的顶点为P.
(1)、求证:;(2)、如果 , 且是与的比例中项,求证:四边形是菱形.24. 如图,直线与x轴交于点A,与y轴交于点C,抛物线经过A、C两点,且与x轴的另一个交点为B,抛物线的顶点为P.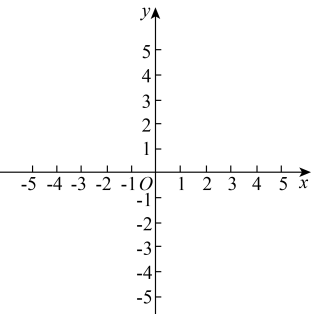 (1)、求抛物线的表达式;(2)、如果抛物线的对称轴与直线交于点D,求的值;(3)、平移这条抛物线,平移后的抛物线交y轴于点E,顶点Q在原抛物线上.当四边形是平行四边形时,求平移后抛物线的表达式.25. 已知:的直径 , C是的中点,D是上的一个动点(不与点A、B、C重合),射线交射线于点E.
(1)、求抛物线的表达式;(2)、如果抛物线的对称轴与直线交于点D,求的值;(3)、平移这条抛物线,平移后的抛物线交y轴于点E,顶点Q在原抛物线上.当四边形是平行四边形时,求平移后抛物线的表达式.25. 已知:的直径 , C是的中点,D是上的一个动点(不与点A、B、C重合),射线交射线于点E.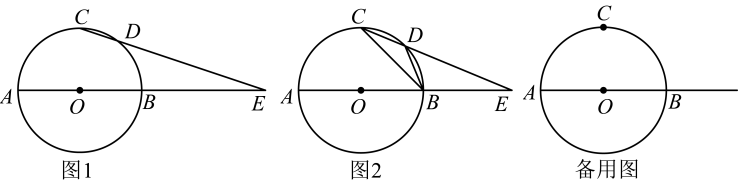 (1)、如图1,当 , 求线段的长;(2)、如图2,当点D在上运动时,连接中是否存在度数保持不变的角?如果存在,请指出这个角并求其度数;如果不存在,请说明理由;(3)、连接 , 当是以为腰的等腰三角形时,求与面积的比值.
(1)、如图1,当 , 求线段的长;(2)、如图2,当点D在上运动时,连接中是否存在度数保持不变的角?如果存在,请指出这个角并求其度数;如果不存在,请说明理由;(3)、连接 , 当是以为腰的等腰三角形时,求与面积的比值.