上海市金山区2023年中考二模数学试卷
试卷更新日期:2023-05-25 类型:中考模拟
一、单选题
-
1. 的相反数为( )A、 B、6 C、 D、2. 单项式的系数是( )A、 B、2 C、3 D、83. 下表是世界卫生组织统计的5种新冠疫苗对新冠病毒防御的有效率的数据统计表,那么这5种疫苗对新冠防御的有效率的中位数是( )
疫苗名称
克尔来福
阿斯利康
莫德纳
辉瑞
卫星
有效率
79.2%
75.9%
95.0%
95.0%
92.3%
A、75.9% B、79.2% C、95.0% D、92.3%4. 已知函数( , 为常数)的函数值随值的增大而减小,那么这个函数图象可能经过的点是( )A、 B、 C、 D、5. 下列图形中,是中心对称图形且旋转后能与自身重合的图形是( )A、等边三角形 B、正方形 C、正八边形 D、正十二边形6. 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知 , 那么球的半径长是( ) A、4 B、5 C、6 D、8
A、4 B、5 C、6 D、8二、填空题
-
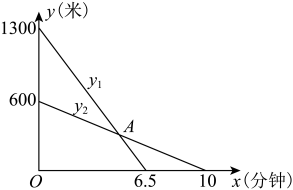
7. 计算 .8. 已知 , 那么 .9. 因式分解:a3-a=.10. 分式方程的解是 .11. 不等式组的解集是 .12. 抛物线在轴的右侧呈趋势(填“上升”或者“下降”).13. 已知关于x的方程x2+3x+m=0有两个相等的实数根,则m的值为 .14. 一个不透明的袋中装有除颜色外大小形状都相同的三种球,其中红球、黄球、黑球的个数之比为 . 从袋子中任意摸出1个球,结果是红球的概率为 .15. 小明和小亮的家分别位于新华书店东、西两边,他们相约同时从家出发到新华书店购书,小明骑车、小亮步行,小明、小亮离新华书店的距离(米)、(米)与时间(分钟)之间的关系如图所示,在途中,当小明、小亮离书店的距离相同时,那么他们所用的时间是分钟.
 16. 如图,已知、分别是的边、上的点,且 , 联结 , 如果 , , 当时,那么 . (用含、的式子表示)
16. 如图,已知、分别是的边、上的点,且 , 联结 , 如果 , , 当时,那么 . (用含、的式子表示) 17. 如图,已知、是的中线,和交于点 , 当时,那么的值等于 .
17. 如图,已知、是的中线,和交于点 , 当时,那么的值等于 .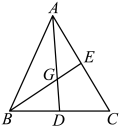 18. 已知中, , , , 点是线段上的动点,点在线段上,如果点关于直线对称的点恰好落在线段上,那么的最大值为 .
18. 已知中, , , , 点是线段上的动点,点在线段上,如果点关于直线对称的点恰好落在线段上,那么的最大值为 .三、解答题
-
19. 计算: .20. 解方程组: .21. 如图,已知在中, , , 点、分别是、的中点,过点作交的延长线于点 , 连接 .
 (1)、求的正弦值;(2)、求线段的长.22. 空气质量指数(Air Quality Index,缩写AQI)是定量描述空气状况的非线性无量纲指数.其数值越大、级别和类别越高,说明空气污染状况越严重,对人体的健康危害也就越大,适用于表示某地区的短期空气质量状况和变化趋势.(空气污染指数为0~50是优;空气污染指数为50~100是良好;空气污染指数为100~150是轻度污染;空气污染指数为150~200是中度污染;空气污染指数为200~250是重度污染.)
(1)、求的正弦值;(2)、求线段的长.22. 空气质量指数(Air Quality Index,缩写AQI)是定量描述空气状况的非线性无量纲指数.其数值越大、级别和类别越高,说明空气污染状况越严重,对人体的健康危害也就越大,适用于表示某地区的短期空气质量状况和变化趋势.(空气污染指数为0~50是优;空气污染指数为50~100是良好;空气污染指数为100~150是轻度污染;空气污染指数为150~200是中度污染;空气污染指数为200~250是重度污染.)如图表示的是某地区2022年11月份30天日均AQI指数的频率分布直方图.
空气质量指数(AQI)
0~50
50~100
100~150
150~200
200~250
天数
3
3
3
频率
0.1
0.1
0.1
(注:每组数据可含最高值,不含最低值)
 (1)、请你根据上述频率分布直方图及表格完成下面的填空:
(1)、请你根据上述频率分布直方图及表格完成下面的填空:这个地区11月份空气为轻度污染的天数是天.;;; .
(2)、为了进一步改善生活环境和空气质量,提高人民的生活质量,当地政府计划从2023年开始增加绿化面积.已知2022年底该地区的绿化面积为20万亩,如果到2024年底,该地区的绿化面积比为2022年的绿化面积增加了50%,假设这两年绿化面积的年增长率相同,求这两年中绿化面积每年的增长率(精确到0.01)(参考数据: , , , )23. 如图,已知是等边三角形,过点作(),且 , 联结、 . (1)、求证:四边形是等腰梯形;(2)、点在腰上,联结交于点 , 若 , 求证: .
(1)、求证:四边形是等腰梯形;(2)、点在腰上,联结交于点 , 若 , 求证: .

