福建厦门集美区2022-2023学年五年级下学期数学学科期中闯关练习
试卷更新日期:2023-05-25 类型:期中考试
一、选择题(共36分)
-
1. 既是2和5的倍数,又是3的倍数的最大两位数是( )。A、75 B、90 C、95 D、962. 冬冬在一个长方体盒子中装了一些棱长为1分米的正方体,这个盒子的容积是( )。
 A、11立方分米 B、19立方分米 C、30立方分米 D、无法确定3. 乐乐分别用5个正方体积木搭出如下立体图形,其中表面积最小的是( )。A、
A、11立方分米 B、19立方分米 C、30立方分米 D、无法确定3. 乐乐分别用5个正方体积木搭出如下立体图形,其中表面积最小的是( )。A、 B、
B、 C、
C、 D、
D、 4. 在下面关于算式a÷b=c(a、b、c均为整数,且b≠0)的说法中,正确的是( )。A、a是b的因数 B、a是b的倍数 C、b是a的倍数 D、c是b的因数5. 如图所示,小明从左面观察这个几何体,他看到的图形是( )。
4. 在下面关于算式a÷b=c(a、b、c均为整数,且b≠0)的说法中,正确的是( )。A、a是b的因数 B、a是b的倍数 C、b是a的倍数 D、c是b的因数5. 如图所示,小明从左面观察这个几何体,他看到的图形是( )。 A、
A、 B、
B、 C、
C、 D、
D、 6. 一个长方体长9分米,宽、高都是3分米,把它横截成三个一样大的小正方体,表面积增加了( )。A、18平方分米 B、36平方分米 C、54平方分米 D、72平方米7. 用小正方体搭成如图的大正方体,如果( )块小正方体,剩下图形的表面积最大。
6. 一个长方体长9分米,宽、高都是3分米,把它横截成三个一样大的小正方体,表面积增加了( )。A、18平方分米 B、36平方分米 C、54平方分米 D、72平方米7. 用小正方体搭成如图的大正方体,如果( )块小正方体,剩下图形的表面积最大。 A、拿走任意 B、拿走A C、拿走B D、拿走C8. 当a是自然数时,2a+1一定是( )。A、质数 B、合数 C、奇数 D、偶数9. 有一个音乐钟,每隔一段相等的时间就会发生铃声,已知上午 9:00,9:40,10:20 和 11:00发出铃声,那么下面哪个时刻也会发出铃声?( )A、13:30 B、14:40 C、15:40 D、16:0010. 在20以内的质数中,加上 2 以后结果还是质数的,一共有( )个A、8 B、6 C、4 D、211. 下面四个数都是五位数,其中F=0,M是一位自然数,那么一定能被3和5整除的数是 ( )。A、MMMFM B、MFMFM C、MFFMF D、MFMMF12. 用棱长1厘米的正方体木块,摆成底面积是12平方厘米,高是2厘米的长方体,可以摆成( )种不同的形状。A、1种 B、2种 C、3种 D、4种13. 结果会是奇数的是( )。A、偶数-偶数 B、奇数+奇数 C、奇数×偶数 D、奇数×奇数14. 图1是一个正方体,它的展开图有6个面。图2给出了其中的5个面,从图3的A,B,C,D中选一个,形成正方体的展开图。这个面是( )
A、拿走任意 B、拿走A C、拿走B D、拿走C8. 当a是自然数时,2a+1一定是( )。A、质数 B、合数 C、奇数 D、偶数9. 有一个音乐钟,每隔一段相等的时间就会发生铃声,已知上午 9:00,9:40,10:20 和 11:00发出铃声,那么下面哪个时刻也会发出铃声?( )A、13:30 B、14:40 C、15:40 D、16:0010. 在20以内的质数中,加上 2 以后结果还是质数的,一共有( )个A、8 B、6 C、4 D、211. 下面四个数都是五位数,其中F=0,M是一位自然数,那么一定能被3和5整除的数是 ( )。A、MMMFM B、MFMFM C、MFFMF D、MFMMF12. 用棱长1厘米的正方体木块,摆成底面积是12平方厘米,高是2厘米的长方体,可以摆成( )种不同的形状。A、1种 B、2种 C、3种 D、4种13. 结果会是奇数的是( )。A、偶数-偶数 B、奇数+奇数 C、奇数×偶数 D、奇数×奇数14. 图1是一个正方体,它的展开图有6个面。图2给出了其中的5个面,从图3的A,B,C,D中选一个,形成正方体的展开图。这个面是( ) A、A B、B C、C D、D15. 下面四幅图中,阴影部分与整个图形的关系与下图一致的是( )。
A、A B、B C、C D、D15. 下面四幅图中,阴影部分与整个图形的关系与下图一致的是( )。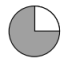 A、
A、 B、
B、 C、
C、 D、
D、 16. 下面阴影部分的面积用分数表示是( )。
16. 下面阴影部分的面积用分数表示是( )。 A、 B、 C、 D、17. 把一个棱长为5厘米的正方体表面涂上红色,然后把它切成棱长为1厘米的小正方体,其中3面涂色的小正方体有( )个。A、8 B、24 C、36 D、4818. 包装两块长7厘米、宽5厘米、厚3厘米的长方体肥皂,包装纸最节省用了( )平方厘米的。A、127 B、214 C、242 D、无法确定
A、 B、 C、 D、17. 把一个棱长为5厘米的正方体表面涂上红色,然后把它切成棱长为1厘米的小正方体,其中3面涂色的小正方体有( )个。A、8 B、24 C、36 D、4818. 包装两块长7厘米、宽5厘米、厚3厘米的长方体肥皂,包装纸最节省用了( )平方厘米的。A、127 B、214 C、242 D、无法确定二、计算(共20分)
-
19. 口算
17.2+2.8= 0.6×0.9= 8÷0.8= 8×1.25= 72.5×3.8×0=
123÷100= 0.74×100= 2.7÷3= 11.5-4.5= 1.4×2.5×4=
20. 递等式计算,能简算要简算①32×125×2.5
②6.72÷2.5÷0.4
③5.4×101
④9.8÷(0.23+1.3×0.2)
⑤[(6.1-4.6)×0.8+0.2]÷0.4
三、解决问题(共42分)
-
21. 动手实践,操作应用
分别画出从正面、上面、左面看到的立体图形的形状。

 22. 亮亮用长方形纸板制作一个长方体。他先把一张长16cm,宽7cm的纸板沿虚线对折,做出了长方体相邻的两个面(如下图),然后再用纸板做出其它4个面,围成长方体。
22. 亮亮用长方形纸板制作一个长方体。他先把一张长16cm,宽7cm的纸板沿虚线对折,做出了长方体相邻的两个面(如下图),然后再用纸板做出其它4个面,围成长方体。 (1)、这个长方体的长是cm、宽是cm、高是cm。(2)、在方格纸上画出这个长方体的右面、上面和前面的形状。(每个小方格的边长代表1cm)
(1)、这个长方体的长是cm、宽是cm、高是cm。(2)、在方格纸上画出这个长方体的右面、上面和前面的形状。(每个小方格的边长代表1cm) 23. 读一读,填一填。
23. 读一读,填一填。“哥德巴赫猜想”是数学中一个著名的难题。中国从20世纪三十年代开始就着手这项研究工作。新中国成立后,更是取得了一定的成果。1973年,我国数学家陈景润发表了一篇题为“大偶数表示为一个质数及一个不超过两个质数的乘积之和”的文章,简称为(1+2),把“哥德巴赫猜想”的论证大大向前推进了一步,陈景润的发现也被誉为“陈景润定理”。
上文中划横线的这句话意思是:大偶数可以表示为两个质数的和,或者可以表示为一个质数及两个质数的乘积的和。如:32=3+29或者32=11+3×7=7+5×5,且答案不唯一。
按照上面的解释,写出关于42的两组不同的等式。
42=( )+( ) 42=( )+( )×( )
24. 妈妈给奶奶买了一件母亲节礼物,她用丝带把礼物按照下图方法捆扎,打结处需要45厘米。捆扎这个礼物一共需要多少厘米丝带? 25. 两个质数的和是50,这两个质数乘积的最大值是多少?26. 学校操场上挖了一个长6米、宽2.5米、深0.6米的沙坑。(1)、这个沙坑的占地面积是多少平方米?(2)、用8.5立方米的黄沙,能不能把这个沙坑填满?27. 四名同学合作进行了如下实验:
25. 两个质数的和是50,这两个质数乘积的最大值是多少?26. 学校操场上挖了一个长6米、宽2.5米、深0.6米的沙坑。(1)、这个沙坑的占地面积是多少平方米?(2)、用8.5立方米的黄沙,能不能把这个沙坑填满?27. 四名同学合作进行了如下实验:步骤1:小明准备了一个长方体玻璃缸。并从里面测量出玻璃缸的长是2.5dm,宽是2dm。高是6dm。
步骤2:小兰往玻璃缸中倒入了10 L的水。
步骤3:小红把这块正方体铁块放入玻璃缸中,发现水正好能淹没这块正方体铁块。
步骤4:小强测出水面上升了1.2dm。
请你根据他们的测量结果,算出小兰倒入水后,水面的高度离容器口有多少分米?
如何计算铁块的体积?
四、思维拓展(共10分)
-
28. 如图,现有空的长方体容器A和水深18厘米的长方体容器B,要将容器B中的水倒入容器A中,使两容器内水的高度相同,这时水的高度是多少厘米?
