上海市崇明区2023年中考二模数学试卷

试卷更新日期：2023-05-25 类型：中考模拟

进入出卷网下载

一、单选题

1. －6的绝对值是（）

A、-6 B、6 C、- $\frac{1}{6}$ D、 $\frac{1}{6}$

查看试题解析
2. 下列运算中，计算结果正确的是（）

A、 ${(2 a^{3})}^{2} = 4 a^{6}$ B、 ${(a + 2 b)}^{2} = a^{2} + 2 a b + 4 b^{2}$ C、 $a^{6} \div a^{3} = a^{2}$ D、 $3 a^{2} - a^{2} = 3$

查看试题解析
3. 如果函数 $y = \frac{1}{2} x + m$ 的图像经过第一、三、四象限，那么m的取值范围是（）

A、 $m > 0$ B、 $m \geq 0$ C、 $m < 0$ D、 $m \leq 0$

查看试题解析
4. 如图是小明某一天测得的7次体温情况的折线统计图，下列信息不正确的是（）

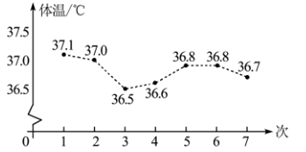A、测得的最高体温为37.1℃ B、前3次测得的体温在下降 C、这组数据的众数是36.8 D、这组数据的中位数是36.6

查看试题解析
5. 下列命题是真命题的是（）

A、四边都相等的四边形是正方形 B、一组邻边相等的矩形是正方形 C、对角线互相垂直平分的四边形是正方形 D、对角线互相垂直且相等的四边形是正方形

查看试题解析
6. 已知在 $△ A B C$ 中， $A B = A C = 5$ ， $B C = 6$ ，如果以A为圆心r为半径的 $⊙ A$ 和以 $B C$ 为直径的 $⊙ D$ 相交，那么r的取值范围（）

A、 $1 < r < 4$ B、 $4 < r < 10$ C、 $1 < r < 7$ D、 $7 < r < 10$

查看试题解析

二、填空题

7. $- 8$ 的立方根是．

查看试题解析
8. 已知 $f (x) = \frac{\sqrt{6}}{x}$ ，那么 $f (\sqrt{2}) =$ ．

查看试题解析
9. 不等式组 ${\begin{array}{l} x - 1 \geq 0 \\ 2 x - 3 < x \end{array}$ 的解集是．

查看试题解析
10. 方程 $\sqrt{x + 2} = x$ 的根是．

查看试题解析
11. 已知关于x的一元二次方程 $x^{2} - 2 x - m = 0$ 没有实数根，那么m的取值范围为．

查看试题解析
12. 已知一个反比例函数图象经过点 $P (- 2 ， 3)$ ，则该反比例函数的图象在各自的象限内，函数值y随自变量x的值逐渐增大而．（填“增大”或“减小”）

查看试题解析
13. 在六张卡片上分别写有6， $- \frac{22}{7}$ ， 3.1415， $\sqrt{3}$ ， 0， $\sin 45 °$ 六个数，从中随机抽取一张，卡片上的数为无理数的概率是．

查看试题解析
14. 为了进一步了解某校九年级学生的体能情况，随机抽取50名学生进行1分钟跳绳次数测试，以测试数据为样本，绘制成不完整的频数分布直方图（如图所示）（每组数据含最小值，不含最大值），若该校九年级共有450名学生，那么一分钟跳绳次数在120～140次的人数是．

查看试题解析
15. 正八边形的每个外角为度．

查看试题解析
16. 已知梯形 $A B C D$ 中， $A D ∥ B C$ ， $B C = 2 A D$ ，设 $\vec{A B} = \vec{a}$ ， $\vec{A D} = \vec{b}$ ，那么 $\vec{D C}$ 可用 $\vec{a}$ 、 $\vec{b}$ 表示为．

查看试题解析
17. 如图， $△ A B C$ 和 $△ A D E$ 都是等边三角形，点D是 $△ A B C$ 的重心，那么 $\frac{S_{△ A D E}}{S_{△ A B C}} =$ ．

查看试题解析
18. 如图，已知在两个直角顶点重合的Rt△ABC和Rt△CDE中， $∠ A C B = ∠ D C E = 90 °$ ， $∠ C A B = ∠ C D E = 30 °$ ， $B C = 3$ ， $C E = 2$ ，将 $△ C D E$ 绕着点C顺时针旋转，当点D恰好落在 $A B$ 边上时，联结 $B E$ ，那么 $B E =$ ．

查看试题解析

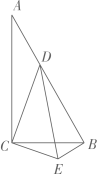
三、解答题

19. 计算： ${(\frac{1}{2})}^{- 2} - π^{0} + \frac{2}{\sqrt{2} - 1} - 8^{\frac{1}{2}}$

查看试题解析
20. 解方程组： ${\begin{array}{l} 2 x - y = 6 ① \\ x^{2} - x y - 2 y^{2} = 0 ② \end{array}$

查看试题解析
21. 如图，已知在 $△ A B C$ 中， $A C = \sqrt{21}$ ， $B C = 6$ ， $⊙ O$ 经过 $△ A B C$ 的顶点A、C，交 $A B$ 边于点D， $A D = 4 \sqrt{3}$ ，点C是 $\overset{⌢}{A D}$ 的中点．

(1)、求 $⊙ O$ 的半径长；

(2)、联结 $D C$ ，求 $\sin ∠ B C D$ ．

查看试题解析
22. 在疫情防控常态化的背景下，某学校为了定期做好专用教室的消毒工作，计划购买甲、乙两种类型的消毒剂，预计购进乙种类型消毒剂的数量y（瓶）与甲种类型消毒剂的数量x（瓶）之间的函数关系如图所示．

(1)、求y关于x的函数解析式（不必写出自变量x的取值范围）；

(2)、该学校用2100元选购了甲种类型的消毒剂，用2400元选购了乙种类型的消毒剂，甲种消毒剂的单价比乙种消毒剂的单价贵30元，求选购的甲、乙消毒剂的数量．

查看试题解析
23. 已知：如图，在平行四边形 $A B C D$ 中，对角线 $A C$ 、 $B D$ 交于E，M是边 $D C$ 延长线上的一点，联结 $A M$ ，与边 $B C$ 交于F，与对角线 $B D$ 交于点G．

(1)、求证： $A G^{2} = G F \cdot G M$ ；

(2)、联结 $C G$ ，如果 $∠ B A G = ∠ B C G$ ，求证：平行四边形 $A B C D$ 是菱形．

查看试题解析
24. 如图，在直角坐标平面 $x O y$ 中，直线 $y = - x + 5$ 分别与x轴、y轴交于A、B两点，抛物线 $y = x^{2} + b x + c$ 经过A、B两点，点D是抛物线的顶点．

(1)、求抛物线的解析式及顶点D的坐标；

(2)、抛物线与x轴的另一个交点为C，点 $M (a ， - \frac{7}{4})$ 在抛物线对称轴左侧的图象上，将抛物线向上平移m个单位（ $m > 0$ ），使点M落在 $△ A B C$ 内，求m的取值范围；

(3)、对称轴与直线 $A B$ 交于点E，P是线段AB上的一个动点（P不与E重合），过P作y轴的平行线交原抛物线于点Q，当 $P E = Q D$ 时，求点Q的坐标．

查看试题解析
25. 如图，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 6$ ， $B C = 3$ ．点D是边 $A C$ 上一动点（不与A、C重合），联结 $B D$ ，过点C作 $C F ⊥ B D$ ，分别交 $B D$ 、 $A B$ 于点E、F．

(1)、当 $C D = 2$ 时，求 $∠ A C F$ 的正切值；

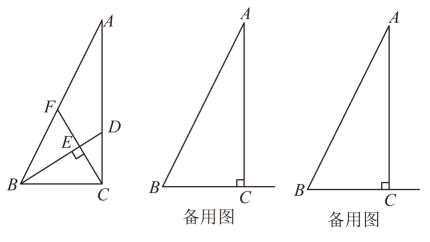(2)、设 $C D = x$ ， $\frac{A F}{B F} = y$ ，求y关于x的函数解析式，并写出x的定义域；

(3)、联结 $F D$ 并延长，与边 $B C$ 的延长线相交于点G，若 $△ D G C$ 与 $△ B A C$ 相似，求 $\frac{A F}{B F}$ 的值．

查看试题解析