辽宁省盘锦市兴隆台区2023年中考一模数学试卷
试卷更新日期:2023-05-25 类型:中考模拟
一、单选题
-
1. 下列各数中与2互为相反数的是( )A、 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数,则该几何体的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 如图所示,将分别含有30°,45°角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为75°,则图中∠α的度数为( )
4. 如图所示,将分别含有30°,45°角的一副三角板重叠,使直角顶点重合,若两直角重叠形成的角为75°,则图中∠α的度数为( ) A、160° B、150° C、140° D、130°5. 在一次学生田径运动会上,参加男子跳高的15名运动员的成绩如表所示:这些运动员跳高成绩的中位数和众数是( )
A、160° B、150° C、140° D、130°5. 在一次学生田径运动会上,参加男子跳高的15名运动员的成绩如表所示:这些运动员跳高成绩的中位数和众数是( )成绩()
1.50
1.60
1.65
1.7
1.75
1.80
人数
1
2
4
3
3
2
A、 B、 C、 D、6. 下列调查中,调查方式选择最合理的是( )A、调查一批飞机零件的合格情况,采用抽样调查 B、检验一批进口罐装饮料的防腐剂含量,采用全面调查 C、企业招聘人员,对应聘人员进行面试,采用抽样调查 D、调查长江的水质情况,采用抽样调查7. 如图,把剪成三部分,边放在同一直线上,点都落在直线上,直线 . 在中,若 , 则的度数为( ) A、70° B、75° C、80° D、85°8. 如图,在中, , Q是上一动点,过点Q作于M,于N, , 则的长是( )
A、70° B、75° C、80° D、85°8. 如图,在中, , Q是上一动点,过点Q作于M,于N, , 则的长是( )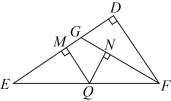 A、定值 B、定值 C、不确定 D、定值9. 如图,A是双曲线上的一点,点C是的中点,过点C作y轴的垂线,垂足为D,交双曲线于点B,且的面积是4,则( )
A、定值 B、定值 C、不确定 D、定值9. 如图,A是双曲线上的一点,点C是的中点,过点C作y轴的垂线,垂足为D,交双曲线于点B,且的面积是4,则( ) A、4 B、6 C、8 D、1010. 如图,在矩形ABCD中, , , 动点P沿折线运动到点B,同时动点Q沿折线运动到点C,点P,Q在矩形边上的运动速度为每秒1个单位长度,点P,Q在矩形对角线上的运动速度为每秒2个单位长度.设运动时间为t秒,的面积为S,则下列图象能大致反映S与t之间函数关系的是( )
A、4 B、6 C、8 D、1010. 如图,在矩形ABCD中, , , 动点P沿折线运动到点B,同时动点Q沿折线运动到点C,点P,Q在矩形边上的运动速度为每秒1个单位长度,点P,Q在矩形对角线上的运动速度为每秒2个单位长度.设运动时间为t秒,的面积为S,则下列图象能大致反映S与t之间函数关系的是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 若在实数范围内有意义,则x的取值范围是 .12. 分解因式: .13. 在平面直角坐标系xOy中,点P(2,a)在正比例函数 的图象上,则点Q(a,3a﹣5)位于第象限.14. 如图正六边形ABCDEF内接于⊙O,在圆形纸片上作随机扎针试验,针头扎在阴影区域内的概率是 .
 15. 已知函数的图象与x轴有交点,则k的取值范围是 .16. 若点的坐标为 , 其中满足不等式组 , 则点的坐标为: .17. 如图,在Rt△ABC中,∠C=90°,分别以A,B为圆心,大于的长为半径画弧,两弧交于点M,N,作直线MN交AB于点D,点E,F分别在边AC,BC上,连接EF.若∠EDF=90°,AE=3,BF=6,则线段EF的长为 .
15. 已知函数的图象与x轴有交点,则k的取值范围是 .16. 若点的坐标为 , 其中满足不等式组 , 则点的坐标为: .17. 如图,在Rt△ABC中,∠C=90°,分别以A,B为圆心,大于的长为半径画弧,两弧交于点M,N,作直线MN交AB于点D,点E,F分别在边AC,BC上,连接EF.若∠EDF=90°,AE=3,BF=6,则线段EF的长为 . 18. 如图,正方形 的对角线相交于点 ,点 在边 上,点 在 的延长线上, , 交 于点 , , ,则 .
18. 如图,正方形 的对角线相交于点 ,点 在边 上,点 在 的延长线上, , 交 于点 , , ,则 .
三、解答题
-
19. 先化简,再求代数式的值. , 其中 , 请你取一个合适的数作为的值代入求值.20. 2022年3月23日,“天宫课堂”第二课开讲.“太空教师”翟志刚、王亚平、叶光富在中国空间站为广大青少年又一次带来了精彩的太空科普课.为了激发学生的航天兴趣,某校举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分为如下5组(满分100分),A组: , B组: , C组: , D组: , E组: , 并绘制了如下不完整的统计图.请结合统计图,解答下列问题:
 (1)、本次调查一共随机抽取了名学生的成绩,频数分布直方图中 , 所抽取学生成绩的中位数落在组;(2)、补全学生成绩频数分布直方图;(3)、若成绩在90分及以上为优秀,学校共有3000名学生,估计该校成绩优秀的学生有多少人?(4)、学校将从获得满分的5名同学(其中有两名男生,三名女生)中随机抽取两名,参加周一国旗下的演讲,请利用树状图或列表法求抽取同学中恰有一名男生和一名女生的概率.21. 如图,一次函数的图像与反比例函数的图像交于点、 , 与轴交于点 , 与轴交于点 . 过点作轴于点 , , 连接 , 已知的面积等于6,点的坐标为 , 点的坐标为 .
(1)、本次调查一共随机抽取了名学生的成绩,频数分布直方图中 , 所抽取学生成绩的中位数落在组;(2)、补全学生成绩频数分布直方图;(3)、若成绩在90分及以上为优秀,学校共有3000名学生,估计该校成绩优秀的学生有多少人?(4)、学校将从获得满分的5名同学(其中有两名男生,三名女生)中随机抽取两名,参加周一国旗下的演讲,请利用树状图或列表法求抽取同学中恰有一名男生和一名女生的概率.21. 如图,一次函数的图像与反比例函数的图像交于点、 , 与轴交于点 , 与轴交于点 . 过点作轴于点 , , 连接 , 已知的面积等于6,点的坐标为 , 点的坐标为 . (1)、请直接写出一次函数的关系式为 ,反比例函数的关系式为;(2)、若点是点关于轴的对称点,求的面积;(3)、根据图像直接写出关于的不等式的解集是 .22. 第24届冬季奥林匹克运动会于今年2月4日至20日在北京举行,我国冬奥选手取得了9块金牌、4块银牌、2块铜牌,为祖国赢得了荣誉,激起了国人对冰雪运动的热情.某地模仿北京首钢大跳台建了一个滑雪大跳台(如图),它由助滑坡道、弧形跳台、着陆坡、终点区四部分组成.图是其示意图,已知:助滑坡道米,弧形跳台的跨度米,顶端到的距离为40米, , , , .求此大跳台最高点距地面的距离是多少米(结果保留整数).(参考数据: , , , , , , , , )
(1)、请直接写出一次函数的关系式为 ,反比例函数的关系式为;(2)、若点是点关于轴的对称点,求的面积;(3)、根据图像直接写出关于的不等式的解集是 .22. 第24届冬季奥林匹克运动会于今年2月4日至20日在北京举行,我国冬奥选手取得了9块金牌、4块银牌、2块铜牌,为祖国赢得了荣誉,激起了国人对冰雪运动的热情.某地模仿北京首钢大跳台建了一个滑雪大跳台(如图),它由助滑坡道、弧形跳台、着陆坡、终点区四部分组成.图是其示意图,已知:助滑坡道米,弧形跳台的跨度米,顶端到的距离为40米, , , , .求此大跳台最高点距地面的距离是多少米(结果保留整数).(参考数据: , , , , , , , , ) 23. 如图,内接于 , 、是的直径,E是长线上一点,且.
23. 如图,内接于 , 、是的直径,E是长线上一点,且.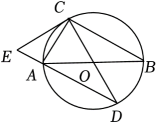 (1)、判断与的位置关系,并说明理由;(2)、若 , , 求线段的长.24. 为增强民众生活幸福感,市政府大力推进老旧小区改造工程.和谐小区新建一小型活动广场,计划在的绿化带上种植甲乙两种花卉.市场调查发现:甲种花卉种植费用y(元)与种植面积之间的函数关系如图所示,乙种花卉种植费用为15元 .
(1)、判断与的位置关系,并说明理由;(2)、若 , , 求线段的长.24. 为增强民众生活幸福感,市政府大力推进老旧小区改造工程.和谐小区新建一小型活动广场,计划在的绿化带上种植甲乙两种花卉.市场调查发现:甲种花卉种植费用y(元)与种植面积之间的函数关系如图所示,乙种花卉种植费用为15元 . (1)、当时,求y与x的函数关系式,并写出x的取值范围;(2)、当甲种花卉种植面积不少于 , 且乙种花卉种植面积不低于甲种花卉种植面积的3倍时.如何分配甲乙两种花卉的种植面积才能使种植的总费用w(元)最少?最少是多少元?25. 问题提出:如图(1),中, , 是的中点,延长至点 , 使 , 延长交于点 , 探究的值.
(1)、当时,求y与x的函数关系式,并写出x的取值范围;(2)、当甲种花卉种植面积不少于 , 且乙种花卉种植面积不低于甲种花卉种植面积的3倍时.如何分配甲乙两种花卉的种植面积才能使种植的总费用w(元)最少?最少是多少元?25. 问题提出:如图(1),中, , 是的中点,延长至点 , 使 , 延长交于点 , 探究的值. (1)、先将问题特殊化.如图(2),当时,直接写出的值;(2)、再探究一般情形.如图(1),证明(1)中的结论仍然成立.(3)、问题拓展:如图(3),在中, , 是的中点,是边上一点, , 延长至点 , 使 , 延长交于点 . 直接写出的值(用含的式子表示).26. 如图,已知抛物线y=ax2+bx+5与x轴交于A(﹣1,0),B(5,0)两点(点A在点B的左侧),与y轴交于点C.
(1)、先将问题特殊化.如图(2),当时,直接写出的值;(2)、再探究一般情形.如图(1),证明(1)中的结论仍然成立.(3)、问题拓展:如图(3),在中, , 是的中点,是边上一点, , 延长至点 , 使 , 延长交于点 . 直接写出的值(用含的式子表示).26. 如图,已知抛物线y=ax2+bx+5与x轴交于A(﹣1,0),B(5,0)两点(点A在点B的左侧),与y轴交于点C. (1)、求抛物线的解析式;(2)、点D是第一象限内抛物线上的一个动点(与点C,B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连接BD,直线BC能否把△BDF分成面积之比为2:3的两部分?若能,请求出点D的坐标;若不能,请说明理由.(3)、若M为抛物线对称轴上一动点,使得△MBC为直角三角形,请直接写出点M的坐标.
(1)、求抛物线的解析式;(2)、点D是第一象限内抛物线上的一个动点(与点C,B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连接BD,直线BC能否把△BDF分成面积之比为2:3的两部分?若能,请求出点D的坐标;若不能,请说明理由.(3)、若M为抛物线对称轴上一动点,使得△MBC为直角三角形,请直接写出点M的坐标.