辽宁省葫芦岛市龙港区2023年中考二模数学试卷
试卷更新日期:2023-05-25 类型:中考模拟
一、单选题
-
1. 下列各数中,最小的是( )A、 B、 C、 D、2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
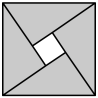 B、
B、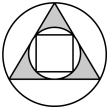 C、
C、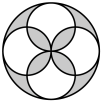 D、
D、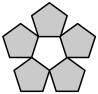 3. 下列运算正确的是( )A、 B、 C、 D、4. 如图所示的几何体的主视图是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 如图所示的几何体的主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 下列事件中,是确定事件的是( )A、掷一枚硬币,正面朝上 B、三角形的内角和是 C、明天会下雨 D、明天的数学测验,小明会得满分6. 青少年身体健康问题越来越引起社会的广泛关注,如表是某班名同学一周体育锻炼时间的统计表:
5. 下列事件中,是确定事件的是( )A、掷一枚硬币,正面朝上 B、三角形的内角和是 C、明天会下雨 D、明天的数学测验,小明会得满分6. 青少年身体健康问题越来越引起社会的广泛关注,如表是某班名同学一周体育锻炼时间的统计表:锻炼时间小时
学生人数人
17
5
则这些学生一周参加体育锻炼时间的众数和中位数分别是( )
A、 , B、 , C、 , D、 ,7. 如图所示,一副三角板叠放在一起,则图中的度数为( ) A、 B、 C、 D、8. 我国古代数学著作算法统宗中有这样一道题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺,绳长,井深各几何?意思是:用绳子测水井的深度,如果将绳子折成3等份,井外余绳4尺;如果将绳子折成4等份,井外余绳1尺,问绳长、井深各是多少尺?设井深x尺,绳长y尺,则所列方程组正确的是( )A、 B、 C、 D、9. 如图,中, , , 分别以点 , 为圆心,大于长为半径作弧,两弧交于点 , , 以为圆心,长为半径作弧,与直线交于点 , 与交于点 , 若 , 则的长为( )
A、 B、 C、 D、8. 我国古代数学著作算法统宗中有这样一道题:以绳测井,若将绳三折测之,绳多四尺;若将绳四折测之,绳多一尺,绳长,井深各几何?意思是:用绳子测水井的深度,如果将绳子折成3等份,井外余绳4尺;如果将绳子折成4等份,井外余绳1尺,问绳长、井深各是多少尺?设井深x尺,绳长y尺,则所列方程组正确的是( )A、 B、 C、 D、9. 如图,中, , , 分别以点 , 为圆心,大于长为半径作弧,两弧交于点 , , 以为圆心,长为半径作弧,与直线交于点 , 与交于点 , 若 , 则的长为( ) A、 B、 C、 D、10. 如图,在 , , , 点从点出发,沿的路径运动,过点作于点 , 连接 , 设点运动的路程为 , 的面积为 , 则能反映和之间关系的图象是( )
A、 B、 C、 D、10. 如图,在 , , , 点从点出发,沿的路径运动,过点作于点 , 连接 , 设点运动的路程为 , 的面积为 , 则能反映和之间关系的图象是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
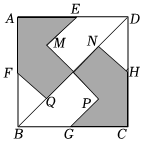
11. 联合国世界人口展望报告指出:到年末,全球人口将达到人,数据用科学记数法表示为 .12. 分解因式: .13. 已知点 , 点 , 若轴,则 .14. 如图,正方形纸板中,点 , , , 分别为 , , , 中点,于点 , 于点 , 于点 , 于点 , 小明随机向纸板内投掷飞镖一次,则飞镖落在阴影部分的概率是 .
 15. 将直线向下平移个单位,得到的图象与轴的交点坐标为 .16. 如图,中, , 点为中点,的延长线交轴于点 , 轴,过点作 , 垂足为点 , 反比例函数的图象经过点 , 若阴影部分面积为 , 则的值为 .
15. 将直线向下平移个单位,得到的图象与轴的交点坐标为 .16. 如图,中, , 点为中点,的延长线交轴于点 , 轴,过点作 , 垂足为点 , 反比例函数的图象经过点 , 若阴影部分面积为 , 则的值为 . 17. 如图,中, , , 点在直线上运动,连接 , 以为斜边作 , 使 , 连接 , 若 , 则的长为 .
17. 如图,中, , , 点在直线上运动,连接 , 以为斜边作 , 使 , 连接 , 若 , 则的长为 . 18. 如图,矩形中, , , 点在的延长线上, , 连接交于点 , 点在边上, , 连接 , 点为中点,连接交于点 , 下列结论:①;②;③;④四边形的面积为 , 其中所有正确结论的序号为 .
18. 如图,矩形中, , , 点在的延长线上, , 连接交于点 , 点在边上, , 连接 , 点为中点,连接交于点 , 下列结论:①;②;③;④四边形的面积为 , 其中所有正确结论的序号为 .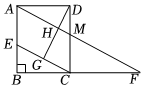
三、解答题
-
19. 先化简,再求值: , 其中 .20. 某中学为纪念“五一劳动节”,组织学生开展了书画展评活动,全校征集学生书画作品.王老师从全校18个班中随机抽取了A、B、C、D四个班,对征集作品进行了数量分析统计,绘制了如下两幅不完整的统计图.
 (1)、王老师采取的调查方式是(填“全面调查”或“抽样调查”);(2)、王老师在所调查的4个班中,共征集到多少件作品?请求出并补全条形统计图;(3)、如果全校参展作品中有4件获得一等奖,其中有1件作品的作者是男生,3件作品的作者是女生.现要从获得一等奖的学生中随机抽取两人去参加学校的总结表彰座谈会,请用树状图或列表的方法,求出恰好抽中一男一女的概率.21. 某商场计划购进一批甲、乙两种消毒液,已知甲种消毒液一瓶的进价与乙种消毒液一瓶的进价的和为40元,用90元购进甲种消毒液的瓶数与用150元购进乙种消毒液的瓶数相同.(1)、求甲、乙两种消毒液每瓶的进价分别是多少元?(2)、若购买甲、乙两种消毒液共50瓶,且总费用不超过1000元,求甲种消毒液至少要购买多少瓶?22. 某海域内一艘轮船从西向东航行到处时发现正东方向有一处暗礁,轮船马上调整方向,沿北偏东航行到点处,然后沿南偏东航行海里到达处,此时恰好在的正东方向.
(1)、王老师采取的调查方式是(填“全面调查”或“抽样调查”);(2)、王老师在所调查的4个班中,共征集到多少件作品?请求出并补全条形统计图;(3)、如果全校参展作品中有4件获得一等奖,其中有1件作品的作者是男生,3件作品的作者是女生.现要从获得一等奖的学生中随机抽取两人去参加学校的总结表彰座谈会,请用树状图或列表的方法,求出恰好抽中一男一女的概率.21. 某商场计划购进一批甲、乙两种消毒液,已知甲种消毒液一瓶的进价与乙种消毒液一瓶的进价的和为40元,用90元购进甲种消毒液的瓶数与用150元购进乙种消毒液的瓶数相同.(1)、求甲、乙两种消毒液每瓶的进价分别是多少元?(2)、若购买甲、乙两种消毒液共50瓶,且总费用不超过1000元,求甲种消毒液至少要购买多少瓶?22. 某海域内一艘轮船从西向东航行到处时发现正东方向有一处暗礁,轮船马上调整方向,沿北偏东航行到点处,然后沿南偏东航行海里到达处,此时恰好在的正东方向. (1)、求 , 两地的距离;结果保留根号(2)、求 , 两地的距离结果保留根号23. “互联网”时代,网上购物备受消费者青睐,某网店销售一款秋季时装,每件成本为元,当售价为元时,每天可销售件,为了吸引更多消费者,该网店决定采取降价措施,调整价格时也要兼顾顾客的利益,根据市场调查发现:销售的数量件与销售单价元之间满足一次函数关系,部分数据如表:
(1)、求 , 两地的距离;结果保留根号(2)、求 , 两地的距离结果保留根号23. “互联网”时代,网上购物备受消费者青睐,某网店销售一款秋季时装,每件成本为元,当售价为元时,每天可销售件,为了吸引更多消费者,该网店决定采取降价措施,调整价格时也要兼顾顾客的利益,根据市场调查发现:销售的数量件与销售单价元之间满足一次函数关系,部分数据如表:销售单价元
销售数量件
(1)、请求出与的函数关系式;(2)、当销售单价是多少元时,若该网店每天获得元的利润?(3)、当销售价格为多少元时,该网店每天可获得最大利润?最大利润是多少元?24. 如图,在中, , , 点在线段上,交于点 , , 与相切于点 . (1)、求证:是的切线;(2)、若 , 求阴影部分的面积.25. 中, , , 点在直线上运动,连接 , 将线段绕点顺时针旋转得到线段 , 连接 , .
(1)、求证:是的切线;(2)、若 , 求阴影部分的面积.25. 中, , , 点在直线上运动,连接 , 将线段绕点顺时针旋转得到线段 , 连接 , . (1)、当点与点重合时,如图 , 请直接写出线段和线段的数量关系;(2)、点在线段上不与点 , 重合时,请写出线段 , , 之间的数量关系,并说明理由;(3)、若 , , 请直接写出的面积.26. 抛物线与轴交于点和点 , 经过点 , 抛物线的对称轴与轴交于点 , 一次函数经过点和点 , 与抛物线的对称轴交于点 .
(1)、当点与点重合时,如图 , 请直接写出线段和线段的数量关系;(2)、点在线段上不与点 , 重合时,请写出线段 , , 之间的数量关系,并说明理由;(3)、若 , , 请直接写出的面积.26. 抛物线与轴交于点和点 , 经过点 , 抛物线的对称轴与轴交于点 , 一次函数经过点和点 , 与抛物线的对称轴交于点 . (1)、求抛物线的解析式;(2)、点在直线上运动点不与点重合 , 当点关于轴的对称点恰好落在抛物线上时,求点的坐标;(3)、长为的线段点位于点的上方在轴上运动 , 连接 , , 若和相似,请直接写出点坐标.
(1)、求抛物线的解析式;(2)、点在直线上运动点不与点重合 , 当点关于轴的对称点恰好落在抛物线上时,求点的坐标;(3)、长为的线段点位于点的上方在轴上运动 , 连接 , , 若和相似,请直接写出点坐标.