辽宁省抚顺市清原县2023年中考一模数学试卷
试卷更新日期:2023-05-25 类型:中考模拟
一、单选题
-
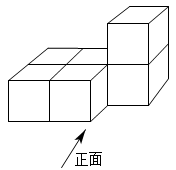
1. 如图,是由6个相同的正方体组成的立体图形,它的俯视图是( )
 A、
A、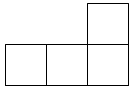 B、
B、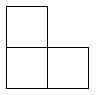 C、
C、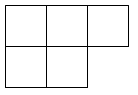 D、
D、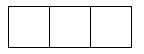 2. 如图①,有6张写有汉字的卡片,它们的背面都相同,现将他们背面朝上洗匀如图②摆放,从中任意翻开一张是汉字“自”的概率是( )
2. 如图①,有6张写有汉字的卡片,它们的背面都相同,现将他们背面朝上洗匀如图②摆放,从中任意翻开一张是汉字“自”的概率是( )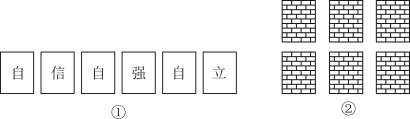 A、 B、 C、 D、3. 如图,某博物馆大厅电梯的截面图中,AB的长为12米,AB与AC的夹角为 ,则高BC是( )
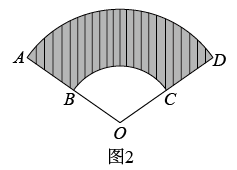
A、 B、 C、 D、3. 如图,某博物馆大厅电梯的截面图中,AB的长为12米,AB与AC的夹角为 ,则高BC是( )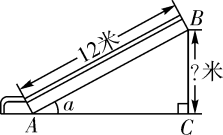 A、 米 B、 米 C、 米 D、 米4. 如图1是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角 形成的扇面,若 , ,则阴影部分的面积为( )
A、 米 B、 米 C、 米 D、 米4. 如图1是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角 形成的扇面,若 , ,则阴影部分的面积为( )
 A、 B、 C、 D、5. 如图,在矩形中, , , 点E、F分别为、的中点,、相交于点G,过点E作 , 交于点H,则线段的长度是( )
A、 B、 C、 D、5. 如图,在矩形中, , , 点E、F分别为、的中点,、相交于点G,过点E作 , 交于点H,则线段的长度是( )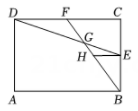 A、 B、1 C、 D、6. 一份摄影作品【七寸照片(长7英寸,宽5英寸)】,现将照片贴在一张矩形衬纸的正中央,照片四周外露衬纸的宽度相同;矩形衬纸的面积为照片面积的3倍.设照片四周外露衬纸的宽度为x英寸(如图),下面所列方程正确的是( )
A、 B、1 C、 D、6. 一份摄影作品【七寸照片(长7英寸,宽5英寸)】,现将照片贴在一张矩形衬纸的正中央,照片四周外露衬纸的宽度相同;矩形衬纸的面积为照片面积的3倍.设照片四周外露衬纸的宽度为x英寸(如图),下面所列方程正确的是( )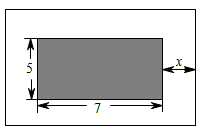 A、 B、 C、 D、7. 如图,在平面直角坐标系中,点P在反比例函数( , )的图象上,其纵坐标为2,过点P作//轴,交x轴于点Q,将线段绕点Q顺时针旋转60°得到线段 . 若点M也在该反比例函数的图象上,则k的值为( )
A、 B、 C、 D、7. 如图,在平面直角坐标系中,点P在反比例函数( , )的图象上,其纵坐标为2,过点P作//轴,交x轴于点Q,将线段绕点Q顺时针旋转60°得到线段 . 若点M也在该反比例函数的图象上,则k的值为( )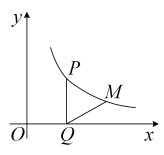 A、 B、 C、 D、48. 已知二次函数 , 当时,y的最小值为 , 则a的值为( )A、或4 B、或 C、或4 D、或49. 如图,在中, , , 以点为圆心,以AB的长为半径作弧交于点D,连接BD,再分别以点 , D为圆心,大于的长为半径作弧,两弧交于点 , 作射线AP交BC于点E,连接DE,则下列结论中不正确的是( )
A、 B、 C、 D、48. 已知二次函数 , 当时,y的最小值为 , 则a的值为( )A、或4 B、或 C、或4 D、或49. 如图,在中, , , 以点为圆心,以AB的长为半径作弧交于点D,连接BD,再分别以点 , D为圆心,大于的长为半径作弧,两弧交于点 , 作射线AP交BC于点E,连接DE,则下列结论中不正确的是( )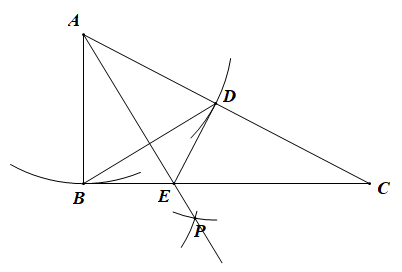 A、 B、垂直平分线段 C、 D、10. 如图,在等边三角形ABC中,BC=4,在Rt△DEF中,∠EDF=90°,∠F=30°,DE=4,点B,C,D,E在一条直线上,点C,D重合,△ABC沿射线DE方向运动,当点B与点E重合时停止运动.设△ABC运动的路程为x,△ABC与Rt△DEF重叠部分的面积为S,则能反映S与x之间函数关系的图象是( )
A、 B、垂直平分线段 C、 D、10. 如图,在等边三角形ABC中,BC=4,在Rt△DEF中,∠EDF=90°,∠F=30°,DE=4,点B,C,D,E在一条直线上,点C,D重合,△ABC沿射线DE方向运动,当点B与点E重合时停止运动.设△ABC运动的路程为x,△ABC与Rt△DEF重叠部分的面积为S,则能反映S与x之间函数关系的图象是( )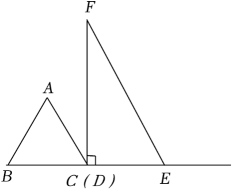 A、
A、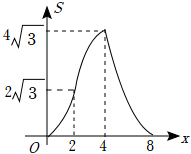 B、
B、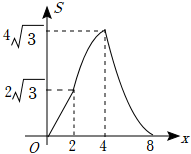 C、
C、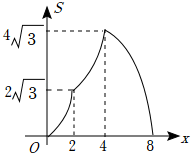 D、
D、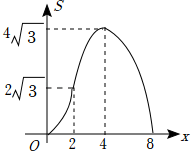
二、填空题
-
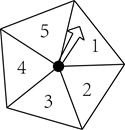
11. 方程 的根是.12. 如图,一个质地均匀的正五边形转盘,指针的位置固定,当转盘自由转动停止后,观察指针指向区域内的数(若指针正好指向分界线,则重新转一次),这个数是一个奇数的概率是.
 13. 一个不透明的口袋中装有5个红球和个黄球,这些球除颜色外都相同,某同学进行了如下试验:从袋中随机摸出1个球记下它的颜色后,放回摇匀,为一次摸球试验.根据记录在下表中的摸球试验数据,可以估计出的值为 .
13. 一个不透明的口袋中装有5个红球和个黄球,这些球除颜色外都相同,某同学进行了如下试验:从袋中随机摸出1个球记下它的颜色后,放回摇匀,为一次摸球试验.根据记录在下表中的摸球试验数据,可以估计出的值为 .摸球的总次数
100
500
1000
2000
…
摸出红球的次数
19
101
199
400
…
摸出红球的频率
0.190
0.202
0.199
0.200
…
14. 如图,已知中,斜边上的高 , , 则 .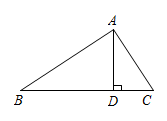 15. 如图,A,B是双曲线y=(x>0)上的两点,连接OA,OB.过点A作AC⊥x轴于点C,交OB于点D.若D为AC的中点,△AOD的面积为3,点B的坐标为(m,2),则m的值为 .
15. 如图,A,B是双曲线y=(x>0)上的两点,连接OA,OB.过点A作AC⊥x轴于点C,交OB于点D.若D为AC的中点,△AOD的面积为3,点B的坐标为(m,2),则m的值为 .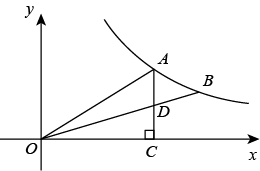 16. 如图所示,小区内有个圆形花坛O,点C在弦AB上,AC=11,BC=21,OC=13,则这个花坛的面积为 . (结果保留)
16. 如图所示,小区内有个圆形花坛O,点C在弦AB上,AC=11,BC=21,OC=13,则这个花坛的面积为 . (结果保留)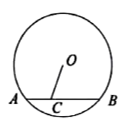 17. 一副三角板按图1放置,是边的中点, . 如图2,将绕点顺时针旋转 , 与相交于点 , 则的长是 .
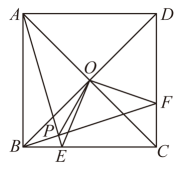
17. 一副三角板按图1放置,是边的中点, . 如图2,将绕点顺时针旋转 , 与相交于点 , 则的长是 .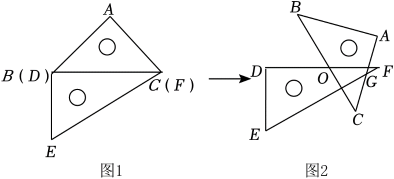 18. 如图,正方形的对角线相交于点O,点F是上一点,交于点E,连接交于点P,连接 , 则下列结论:
18. 如图,正方形的对角线相交于点O,点F是上一点,交于点E,连接交于点P,连接 , 则下列结论:①;
②;
③;
④若 , 则 ;
⑤四边形的面积是正方形面积的 .
其中正确的结论是 .
三、解答题
-
19. 如图,在平面直角坐标系中,各顶点的坐标分别是 , 与关于原点O位似,的对应点分别为 , 其中的坐标是 .
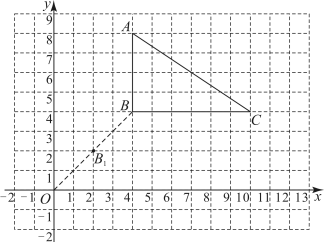 (1)、和的相似比是;(2)、请画出;(3)、边上有一点 , 在边上与点M对应点的坐标是;(4)、的面积是 .20. 据网站调查,2022年网民们关注的热点话题分别有:消费、教育、环保、反腐及其他共五类,根据调查的部分相关数据,绘制的统计图表如下:
(1)、和的相似比是;(2)、请画出;(3)、边上有一点 , 在边上与点M对应点的坐标是;(4)、的面积是 .20. 据网站调查,2022年网民们关注的热点话题分别有:消费、教育、环保、反腐及其他共五类,根据调查的部分相关数据,绘制的统计图表如下: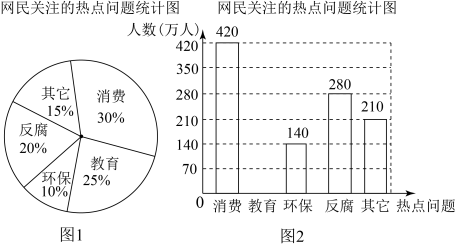 (1)、求出共调查了多少人,并补全条形统计图;(2)、若某市约有880万人口,请你估计最关注环保问题的人数约为多少万人?(3)、在这次调查中,某单位共有里、乙、丙、丁四人最关注教育问题,现准备从这四大中随机抽取两人进行座谈,试用列表法或树形图的方法抽取的两人恰好是甲和乙的概率.21. 如图,直线与反比例函数的图像相交于点A和点 , 与x轴的正半轴相交于点B.
(1)、求出共调查了多少人,并补全条形统计图;(2)、若某市约有880万人口,请你估计最关注环保问题的人数约为多少万人?(3)、在这次调查中,某单位共有里、乙、丙、丁四人最关注教育问题,现准备从这四大中随机抽取两人进行座谈,试用列表法或树形图的方法抽取的两人恰好是甲和乙的概率.21. 如图,直线与反比例函数的图像相交于点A和点 , 与x轴的正半轴相交于点B.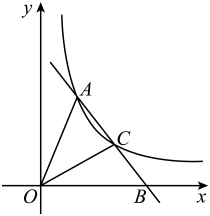 (1)、求k的值;(2)、连接 , 若点C为线段的中点,求的面积.22. 如图1所示是一种太阳能路灯,它由灯杆和灯管支架两部分构成如图2,是灯杆,是灯管支架,灯管支架与灯杆间的夹角.综合实践小组的同学想知道灯管支架的长度,他们在地面的点E处测得灯管支架底部D的仰角为60°,在点F处测得灯管支架顶部C的仰角为30°,测得m,m(A,E,F在同一条直线上).根据以上数据,解答下列问题:
(1)、求k的值;(2)、连接 , 若点C为线段的中点,求的面积.22. 如图1所示是一种太阳能路灯,它由灯杆和灯管支架两部分构成如图2,是灯杆,是灯管支架,灯管支架与灯杆间的夹角.综合实践小组的同学想知道灯管支架的长度,他们在地面的点E处测得灯管支架底部D的仰角为60°,在点F处测得灯管支架顶部C的仰角为30°,测得m,m(A,E,F在同一条直线上).根据以上数据,解答下列问题: (1)、求灯管支架底部距地面高度的长(结果保留根号);(2)、求灯管支架的长度(结果精确到0.1m,参考数据:).23. 如图,已知是的直径,点是上异于 , 的点,点是的中点,连接 , , , 过点作交的延长线于点 , 交的延长线于点 , 的平分线交于点 , 交于点 .
(1)、求灯管支架底部距地面高度的长(结果保留根号);(2)、求灯管支架的长度(结果精确到0.1m,参考数据:).23. 如图,已知是的直径,点是上异于 , 的点,点是的中点,连接 , , , 过点作交的延长线于点 , 交的延长线于点 , 的平分线交于点 , 交于点 . (1)、求证:是的切线;(2)、求的值.24. 为实施“乡村振兴”计划,某村产业合作社种植了“千亩桃园”.2022年该村桃子丰收,销售前对本地市场进行调查发现:当批发价为4千元/吨时,每天可售出12吨,每吨涨1千元,每天销量将减少2吨,据测算,每吨平均投入成本2千元,为了抢占市场,薄利多销,该村产业合作社决定,批发价每吨不低于4千元,不高于5.5千元.请解答以下问题:(1)、求每天销量y(吨)与批发价x(千元/吨)之间的函数关系式,并直接写出自变量x的取值范围;(2)、当批发价定为多少时,每天所获利润最大?最大利润是多少?25. 已知矩形ABCD,点E为直线BD上的一个动点(点E不与点B重合),连接AE,以AE为一边构造矩形AEFG(A,E,F,G按逆时针方向排列),连接DG.
(1)、求证:是的切线;(2)、求的值.24. 为实施“乡村振兴”计划,某村产业合作社种植了“千亩桃园”.2022年该村桃子丰收,销售前对本地市场进行调查发现:当批发价为4千元/吨时,每天可售出12吨,每吨涨1千元,每天销量将减少2吨,据测算,每吨平均投入成本2千元,为了抢占市场,薄利多销,该村产业合作社决定,批发价每吨不低于4千元,不高于5.5千元.请解答以下问题:(1)、求每天销量y(吨)与批发价x(千元/吨)之间的函数关系式,并直接写出自变量x的取值范围;(2)、当批发价定为多少时,每天所获利润最大?最大利润是多少?25. 已知矩形ABCD,点E为直线BD上的一个动点(点E不与点B重合),连接AE,以AE为一边构造矩形AEFG(A,E,F,G按逆时针方向排列),连接DG.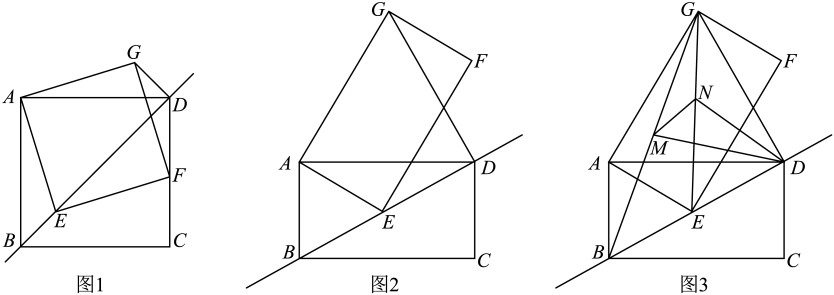 (1)、如图1,当==1时,请直接写出线段BE与线段DG的数量关系与位置关系;(2)、如图2,当==2时,请猜想线段BE与线段DG的数量关系与位置关系,并说明理由;(3)、如图3,在(2)的条件下,连接BG,EG,分别取线段BG,EG的中点M,N,连接MN,MD,ND,若AB= , ∠AEB=45°,请直接写出△MND的面积.26. 如图,已知抛物线: 与x轴交于点A, (A在B的左侧),与y轴交于点C,对称轴是直线 ,P是第一象限内抛物线上的任一点.
(1)、如图1,当==1时,请直接写出线段BE与线段DG的数量关系与位置关系;(2)、如图2,当==2时,请猜想线段BE与线段DG的数量关系与位置关系,并说明理由;(3)、如图3,在(2)的条件下,连接BG,EG,分别取线段BG,EG的中点M,N,连接MN,MD,ND,若AB= , ∠AEB=45°,请直接写出△MND的面积.26. 如图,已知抛物线: 与x轴交于点A, (A在B的左侧),与y轴交于点C,对称轴是直线 ,P是第一象限内抛物线上的任一点.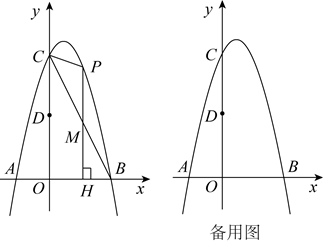 (1)、求抛物线的解析式;(2)、若点D为线段 的中点,则 能否是等边三角形?请说明理由;(3)、过点P作x轴的垂线与线段 交于点M,垂足为点H,若以P,M,C为顶点的三角形与 相似,求点P的坐标.
(1)、求抛物线的解析式;(2)、若点D为线段 的中点,则 能否是等边三角形?请说明理由;(3)、过点P作x轴的垂线与线段 交于点M,垂足为点H,若以P,M,C为顶点的三角形与 相似,求点P的坐标.