辽宁省大连市普兰店区2023年中考一模数学试卷
试卷更新日期:2023-05-25 类型:中考模拟
一、单选题
-
1. 下列图形中,既是中心对称图形,又是轴对称图形的是( )A、平行四边形 B、等边三角形 C、矩形 D、等腰梯形2. 下列立体图形中,主视图是圆的是( )A、
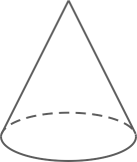 B、
B、 C、
C、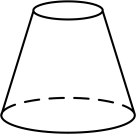 D、
D、 3. 如图,在中,点分别在边上, , 若 , 则 ( )
3. 如图,在中,点分别在边上, , 若 , 则 ( ) A、 B、 C、 D、4. 如图,已知 为 的直径,点C在 上, ,则 的度数为( )
A、 B、 C、 D、4. 如图,已知 为 的直径,点C在 上, ,则 的度数为( ) A、 B、 C、 D、5. 把标号为1,2,3的三个小球放入一个不透明的口袋中,随机摸取一个小球然后放回,再随机摸出一个小球,两次取出的小球的标号的和大于3的概率是( )A、 B、 C、 D、6. 今年以来,我市接待的游客人数逐月增加,据统计,游玩某景区的游客人数三月份为4万人,五月份为万人.设平均每月增长率为x,则可列方程为( )A、 B、 C、 D、7. 某公司计划新建一个容积V(m3)一定的长方体污水处理池,池的底面积S(m2)与其深度h(m)之间的函数关系式为 , 这个函数的图象大致是( )A、
A、 B、 C、 D、5. 把标号为1,2,3的三个小球放入一个不透明的口袋中,随机摸取一个小球然后放回,再随机摸出一个小球,两次取出的小球的标号的和大于3的概率是( )A、 B、 C、 D、6. 今年以来,我市接待的游客人数逐月增加,据统计,游玩某景区的游客人数三月份为4万人,五月份为万人.设平均每月增长率为x,则可列方程为( )A、 B、 C、 D、7. 某公司计划新建一个容积V(m3)一定的长方体污水处理池,池的底面积S(m2)与其深度h(m)之间的函数关系式为 , 这个函数的图象大致是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,将△OAB绕点O逆时针旋转80°,得到△OCD.若∠A=2∠D=100°,则∠α的度数是( )
8. 如图,将△OAB绕点O逆时针旋转80°,得到△OCD.若∠A=2∠D=100°,则∠α的度数是( )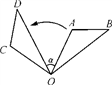 A、50° B、60° C、40° D、30°9. 如图,直线与 , 轴正半轴交于 , 两点,则( )
A、50° B、60° C、40° D、30°9. 如图,直线与 , 轴正半轴交于 , 两点,则( ) A、 B、 C、 D、10. 在学校运动会上,一位运动员掷铅球,铅球的高与水平距离之间的函数关系式为 , 则此运动员的成绩是( )A、 B、 C、 D、
A、 B、 C、 D、10. 在学校运动会上,一位运动员掷铅球,铅球的高与水平距离之间的函数关系式为 , 则此运动员的成绩是( )A、 B、 C、 D、二、填空题
-
11. 方程 的根为.12. 二次函数的顶点坐标是 .13. 一颗质地均匀的骰子,其六个面分别刻有六个数字,投掷这个骰子一次,则向上一面的数字大于的概率是 .14. 一个圆锥的底面圆的半径为 2,母线长为 4,则它的侧面积为 .15. 如图,在平面直角坐标系中,线段 的端点 在 轴正半轴上, 轴,点 在第一象限,函数 ( )的图象交边 于点 ,D为 轴上一点,连结 、 .若 ,则 的面积为.
 16. 如图,中, , , 于D,E是的中点,的延长线交的延长线于F,若 , 则 .
16. 如图,中, , , 于D,E是的中点,的延长线交的延长线于F,若 , 则 .
三、解答题
-
17. 解方程: .18. 有两把不同的锁和四把不同的钥匙,其中两把钥匙恰好分别能打开这两把锁,其余的钥匙不能打开这两把锁.现在任意取出一把钥匙去开任意一把锁.(1)、请用列表或画树状图的方法表示出上述试验所有可能结果;(2)、求一次打开锁的概率.19. 嵊州市三江购物中心为了迎接店庆,准备了某种气球,这些气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如下图所示.
 (1)、试写出这个函数的表达式;(2)、当气球的体积为2m3时,气球内气体的气压是多少?(3)、当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,对气球的体积有什么要求?20. 已知抛物线 .(1)、求证:无论为何值时此抛物线与轴总有两个不同的交点;(2)、若、是抛物线与轴交点的横坐标且 , 求的值.21. 为响应市委市政府提出的建设“绿色襄阳”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地,建成一个矩形花园.要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为532m2 , 那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)
(1)、试写出这个函数的表达式;(2)、当气球的体积为2m3时,气球内气体的气压是多少?(3)、当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,对气球的体积有什么要求?20. 已知抛物线 .(1)、求证:无论为何值时此抛物线与轴总有两个不同的交点;(2)、若、是抛物线与轴交点的横坐标且 , 求的值.21. 为响应市委市政府提出的建设“绿色襄阳”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地,建成一个矩形花园.要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为532m2 , 那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形) 22. 如图,是的直径,点在上, , 过点的切线与的延长线相交于点 , 与相交于点 .
22. 如图,是的直径,点在上, , 过点的切线与的延长线相交于点 , 与相交于点 . (1)、求证:;(2)、若 , , 求的长.23. 2022年我国建成5G基站超60万个,5G建设跑出“中国速度”.某地有一个5G信号塔 , 小敏想用所学的数学知识测量信号塔\的高度,如图,为了测量信号塔的高度,在地平面上点处测得信号塔顶端的仰角为 , 从点向点方向前进2米到点 , 从点测得信号塔底端B的仰角为 , 已知楼房的高度为21米.求信号塔的高度(结果精确到米).(参考数据 , , , , , )
(1)、求证:;(2)、若 , , 求的长.23. 2022年我国建成5G基站超60万个,5G建设跑出“中国速度”.某地有一个5G信号塔 , 小敏想用所学的数学知识测量信号塔\的高度,如图,为了测量信号塔的高度,在地平面上点处测得信号塔顶端的仰角为 , 从点向点方向前进2米到点 , 从点测得信号塔底端B的仰角为 , 已知楼房的高度为21米.求信号塔的高度(结果精确到米).(参考数据 , , , , , ) 24. 已知中, , , , . 点从点出发,沿运动,速度为 , 同时点从点出发,沿运动,运动速度为 , 一个点到达终点,另一点也停止运动.
24. 已知中, , , , . 点从点出发,沿运动,速度为 , 同时点从点出发,沿运动,运动速度为 , 一个点到达终点,另一点也停止运动. (1)、求的长;(2)、设的面积为 , 点运动时间为 , 求与的函数关系式,并写出的取值范围.25. 综合与实践问题情境:数学活动课上,王老师出示了一个问题:如图1,在中, . 求证: .
(1)、求的长;(2)、设的面积为 , 点运动时间为 , 求与的函数关系式,并写出的取值范围.25. 综合与实践问题情境:数学活动课上,王老师出示了一个问题:如图1,在中, . 求证: . (1)、独立思考:请解答王老师提出的问题.(2)、实践探究:在原有问题条件不变的情况下,王老师增加下面的条件,并提出新问题,请你解答.
(1)、独立思考:请解答王老师提出的问题.(2)、实践探究:在原有问题条件不变的情况下,王老师增加下面的条件,并提出新问题,请你解答.“如图2,延长至点E,使 , 延长交的延长线于点F.当时,探究和之间的数量关系,并证明.”
(3)、问题解决:数学活动小组同学对问题(2)进一步研究之后发现,当把“”改为“”时,如图3,求的值.请你解答.26. 如图,抛物线的图像与坐标轴交于三点, (1)、求两点坐标;(2)、如图1,若抛物线的顶点为 , 求与的面积之和;(3)、在抛物线上是否存在点 , 使得 , 若存在,求出点坐标,若不存在,请说明理由.
(1)、求两点坐标;(2)、如图1,若抛物线的顶点为 , 求与的面积之和;(3)、在抛物线上是否存在点 , 使得 , 若存在,求出点坐标,若不存在,请说明理由.