辽宁省大连市金普新区2023年中考一模数学试卷
试卷更新日期:2023-05-25 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、3 C、 D、2. 三棱柱的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 在平面直角坐标系中,将点向右平移5个单位长度得到的点坐标为( )A、 B、 C、 D、4. 下列图形中,既是中心对称又是轴对称图形的是( )A、正三角形 B、菱形 C、平行四边形 D、等腰梯形5. 数字250000用科学记数法表示应为( )A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 某语文教师调查了本班10名学生平均每天的课外阅读时间,统计结果如表所示:
3. 在平面直角坐标系中,将点向右平移5个单位长度得到的点坐标为( )A、 B、 C、 D、4. 下列图形中,既是中心对称又是轴对称图形的是( )A、正三角形 B、菱形 C、平行四边形 D、等腰梯形5. 数字250000用科学记数法表示应为( )A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 某语文教师调查了本班10名学生平均每天的课外阅读时间,统计结果如表所示:课外阅读时间(小时)
1
2
人数
2
3
4
1
那么这10名学生平均每天的课外阅读时间的中位数是( )
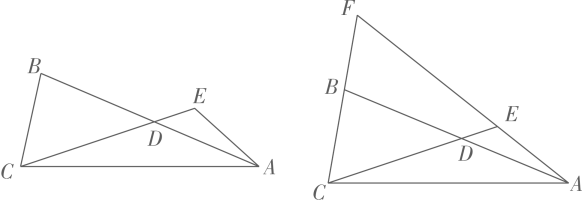
A、 B、1 C、 D、8. 已知一次函数y=kx+3的图像与x轴交于点A(3,0),则k的值为( )A、1 B、3 C、-1 D、-39. 已知实心球运动的高度与水平距离之间的函数关系是 , 则该同学此次投掷实心球的成绩是( )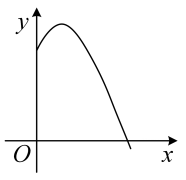 A、 B、 C、 D、10. 如图,菱形的边长为 , , 边在轴上,若将菱形绕点逆时针旋转 , 得到菱形 , 则点的对应点的坐标为( )
A、 B、 C、 D、10. 如图,菱形的边长为 , , 边在轴上,若将菱形绕点逆时针旋转 , 得到菱形 , 则点的对应点的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
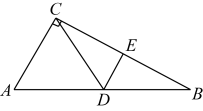
11. 不等式的解集为 .12. 方程的解为 .13. 在一个不透明的袋子里装着1个白球、2个黄球、4个红球,它们除颜色不同外其余都相同.现从袋中任意掵出一个球是红球的概率为.14. 如图,在中, , 的垂直平分线分别交于点D、E,若 , , 则的周长为 .
 15. 菱形周长为40,两条对角线的和为28,则菱形的面积为 .16. 如图,用黑白两种颜色的菱形纸片,按黑色纸片数逐渐增加1的规律拼成下列图案,若第n个图案中有2023个白色纸片,则n的值为 .
15. 菱形周长为40,两条对角线的和为28,则菱形的面积为 .16. 如图,用黑白两种颜色的菱形纸片,按黑色纸片数逐渐增加1的规律拼成下列图案,若第n个图案中有2023个白色纸片,则n的值为 .
三、解答题
-
17. 计算: .18. 为了解学生一周劳动情况,某校随机调查了部分学生的一周累计劳动时间,将他们一周累计劳动时间(单位:h,划分为 , , , 四个组,并将调查结果绘制成如图所示的两幅不完整的统计图.

根据图中所给信息解答下列问题:
(1)、这次抽样调查中,D组有名学生;一共抽取名学生;(2)、已知该校有名学生,根据调查结果,请你估计该校一周累计劳动时间达到3小时及3小时以上的学生共有多少人.19. 如图,在中,点在的延长线上,且 , 与相交于点 . 求证: . 20. 已知8台A型早餐机和3台B型早餐机需要元,6台A型早餐机和1台B型早餐机需要元.问:每台A型早餐机和每台B型早餐机的价格分别是多少元?21. 如图,B港口在A港口的南偏西方向上,距离A港口100海里处.一艘货轮航行到C处,发现A港口在货轮的北偏西方向,B港口在货轮的北偏西方向,求此时货轮与A港口的距离(结果取整数).(参考数据:)
20. 已知8台A型早餐机和3台B型早餐机需要元,6台A型早餐机和1台B型早餐机需要元.问:每台A型早餐机和每台B型早餐机的价格分别是多少元?21. 如图,B港口在A港口的南偏西方向上,距离A港口100海里处.一艘货轮航行到C处,发现A港口在货轮的北偏西方向,B港口在货轮的北偏西方向,求此时货轮与A港口的距离(结果取整数).(参考数据:) 22. 已知某消毒药物燃烧时,室内每立方米空气中的含药量y(微克)与时间x(小时)成正比例,药物熄灭后,y(微克)与x(小时)成反比例,如图所示,现测得药物4小时燃毕,此时室内空气每立方米的含药量为6微克,请你根据题中提供的信息,解答下列问题:
22. 已知某消毒药物燃烧时,室内每立方米空气中的含药量y(微克)与时间x(小时)成正比例,药物熄灭后,y(微克)与x(小时)成反比例,如图所示,现测得药物4小时燃毕,此时室内空气每立方米的含药量为6微克,请你根据题中提供的信息,解答下列问题: (1)、分别求出药物燃烧时和药物熄灭后y关于x的函数关系式;(2)、研究表明,当空气中每立方米的含药量不低于3微克且持续时间不低于10小时时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?23. 如图,在中, , 以为直径的⊙O交于点D,切线交于点E.
(1)、分别求出药物燃烧时和药物熄灭后y关于x的函数关系式;(2)、研究表明,当空气中每立方米的含药量不低于3微克且持续时间不低于10小时时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?23. 如图,在中, , 以为直径的⊙O交于点D,切线交于点E. (1)、求证: .(2)、若 , , 求的长.24. 如图, , , , 点为边上一点且不与A,B重合,点从点出发,向终点A运动,速度为每秒5个单位长度,过点作于点 , 分别过点 , 作 , 的平行线,两条直线交于点 . 设点的运动时间为 , 与重叠部分图形面积为S.
(1)、求证: .(2)、若 , , 求的长.24. 如图, , , , 点为边上一点且不与A,B重合,点从点出发,向终点A运动,速度为每秒5个单位长度,过点作于点 , 分别过点 , 作 , 的平行线,两条直线交于点 . 设点的运动时间为 , 与重叠部分图形面积为S. (1)、当点落在上时,求的值;(2)、求S与t的函数关系式,并直接写出自变量t的取值范围.
(1)、当点落在上时,求的值;(2)、求S与t的函数关系式,并直接写出自变量t的取值范围.