黑龙江省佳木斯市2023年中考一模数学试卷

试卷更新日期：2023-05-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列运算中，计算正确的是（）

A、 ${(a + b)}^{2} = a^{2} + b^{2}$ B、 $\frac{1}{2 a^{- 2}} = 2 a^{2}$ C、 ${(- a^{3})}^{3} = a^{6}$ D、 $a^{4} \div a^{- 2} = a^{6}$

查看试题解析
2. “致中和，天地位焉，万物育焉.”对称美是我国古人和谐平衡思想的体现，常被运用于建筑、器物、绘画、标识等作品的设计上，使对称之美惊艳了千年的时光.在下列与扬州有关的标识或简图中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 学校举办立定跳远比赛，七年级（1）班参加比赛的8名同学立定跳远的成绩（单位：cm）分别是169，171，180，178，182，176，166，176，则这8个数据的中位数是（）

A、181 B、175 C、176 D、177

查看试题解析
4. 如图是由若干个相同的小正方体搭成一个几何体的主视图和俯视图，则所需的小正方体的个数最多是（）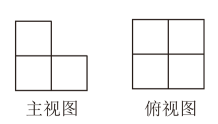

A、6 B、5 C、4 D、3

查看试题解析
5. 黑龙江省中学生排球锦标赛共进行了110场双循环比赛，则参加比赛的队伍共有（）

A、8支 B、9支 C、10支 D、11支

查看试题解析
6. 已知关于x的分式方程 $\frac{m x}{x - 1} - \frac{2}{x - 1} = 1$ 无解，则m的值是（）

A、1 B、1或2 C、0或2 D、0或1

查看试题解析
7. 某班级奖励“德、智、体、美、劳”五育表现优异的学生，计划用不超过100元购买A，B两种笔记本作为奖品，A种笔记本每本8元，B种笔记本每本10元，每种笔记本至少买4本，则购买方案有（）

A、7种 B、8种 C、9种 D、10种

查看试题解析
8. 如图，在平面直角坐标系中，平行四边形 $O A B C$ 的顶点A在反比例函数 $y = \frac{a}{x}$ 的图象上，顶点B在反比例函数 $y = \frac{b}{x}$ 的图象上，点C在x轴的正半轴上，平行四边形 $O A B C$ 的面积是3，则 $a - b$ 的值是（）

A、3 B、 $- 3$ C、5 D、 $- 5$

查看试题解析
9. 如图，P是正方形 $A B C D$ 内一点， $A P = 3 ， B P = 2 ， C P = \sqrt{17}$ ，则正方形 $A B C D$ 的面积是（）

A、 $13 + 6 \sqrt{2}$ B、13 C、 $\sqrt{21}$ D、 $11 + 6 \sqrt{2}$

查看试题解析
10. 如图，在正方形 $A B C D$ 中，E为边 $A B$ 上一点，过点D作 $D F ⊥ D E$ ，与 $B C$ 的延长线交于点F．连接 $E F$ ，与边 $C D$ 交于点G，与对角线 $B D$ 交于点H， $D I ⊥ E F$ 与 $B C$ 相交于点I．下列结论：① $A E = C F$ ；② $E F = \sqrt{2} D F$ ；③ $∠ A D E + ∠ E F B = 45 °$ ；④若 $B F = B D = \sqrt{2}$ ，则 $B E = 2 - \sqrt{2}$ ；⑤连接 $E I$ ，则 $E I = A E + C I$ ．其中结论正确的序号是（）．

A、①②④ B、①②③⑤ C、③④⑤ D、①②③④⑤

查看试题解析

二、填空题

11. 我国经济总量占世界经济的比重稳居世界第二位，国内生产总值已达到114万亿元，将数据114万亿用科学记数法表示为．

查看试题解析
12. 函数y= $\frac{\sqrt{x - 1}}{x + 1}$ 中，自变量x的取值范围是．

查看试题解析
13. 如图，已知四边形ABCD，对角线AC，BD交于点O，AB=CD，请添加一个条件（只添一个即可），使四边形ABCD是平行四边形．

查看试题解析
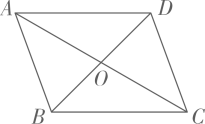14. 一个不透明的口袋中有2个红球和4个白球，这些球除颜第色外其余完全相同，摇匀后随机摸出一个球，摸到白球的概率是．

查看试题解析
15. 若关于x的一元一次不等式组 ${\begin{array}{l} a - 4 x < 0 \\ \frac{2 x - 1}{5} - 1 \leq 0 \end{array}$ 有3个整数解，则a的取值范围是．

查看试题解析
16. 如图， $A B$ 是半 $⊙ O$ 的直径，点C是弧 $A B$ 的中点，点E是弧 $A C$ 的中点，连接 $E B 、 C A$ 交于点F，则 $\frac{E F}{B F} =$ ．

查看试题解析
17. 半径为10cm的半圆围成一个圆锥，则这个圆锥的高是cm．

查看试题解析
18. 如图，菱形ABCD中， $∠ A B C = 60 °$ ，边长为3，P是对角线BD上的一个动点，则 $\frac{1}{2} B P + P C$ 的最小值是．

查看试题解析
19. 在矩形 $A B C D$ 中， $A B = 6$ ， $A D = 15$ ，点 $E$ 在边 $B C$ 上．且 $∠ A E D = 90 °$ ， $P$ 是射线ED上的一个动点．若 $△ A E P$ 是等腰直角三角形，则 $C P$ 的长为．

查看试题解析
20. 如图，在平面直角坐标系中，点 $A_{1} ， A_{2} ， A_{3} ， A_{4} ， \dots$ 在x轴上且 $O A_{1} = 1 ， O A_{2} = 2 O A_{1} ， O A_{3} = 2 O A_{2} ， O A_{4} = 2 O A_{3} ， \dots ，$ 按此规律，过点 $A_{1} ， A_{2} ， A_{3} ， A_{4} ， \dots$ 作x轴的垂线分别与直线 $y = \sqrt{3} x$ 交于点 $B_{1} ， B_{2} ， B_{3} ， B_{4} \dots ．$ 连接 $B_{1} A_{2} ， B_{2} A_{3} ， B_{3} A_{3} ， \dots$ ，记 $△ B_{1} A_{2} B_{2} ， △ B_{2} A_{3} B_{3} ， △ B_{3} A_{4} B_{4} ， \dots$ 的面积分别为 $S_{1} ， S_{2} ， S_{3} ， \dots ，$ 则 $S_{2023} =$ ．

查看试题解析

三、解答题

21. 先化简，再求值： $(1 - \frac{a^{2} - 1}{a^{2} - 3 a}) \div \frac{3 a - 1}{a}$ ，其中 $a = 2 \sin 60 ° + 3$ ．

查看试题解析
22. 如图，在平面直角坐标系中， $△ A B C$ 三个顶点的坐标分别为 $A (0 ， 3)$ ， $B (3 ， 4)$ ， $C (2 ， 2)$ ，将 $△ A B C$ 向左平移3个单位长度，再向下平移4个单位长度得到 $△ A_{1} B_{1} C_{1}$ ．

(1)、画出 $△ A_{1} B_{1} C_{1}$ ，并写出点 $C_{1}$ 的坐标；

(2)、画出将 $△ A_{1} B_{1} C_{1}$ 绕点O按逆时针方向旋转 $90 °$ 后的图形 $△ A_{2} B_{2} C_{2}$ ；

(3)、求 $△ A_{1} B_{1} C_{1}$ 在旋转过程中扫过的面积．

查看试题解析
23. 如图，抛物线 $y = - x^{2} + b x + c$ 经过点 $A (- 1 ， 0)$ 和点 $B (0 ， 3)$ ，顶点为C，D是抛物线上一点．

(1)、求抛物线的解析式和顶点C的坐标；

(2)、若 $S_{Δ B C D} = \frac{3}{2}$ ，请直接写出点D的坐标．

查看试题解析
24. 为进一步落实“双减”工作，某校对部分学生的作业情况进行了问卷调查．设每名学生平均每天完成作业的时间为x小时，其中的分组情况如下：A组： $0 \leq x < 0.5$ ， B组： $0.5 \leq x < 1$ ：C组： $1 \leq x < 1.5$ ：D组： $1.5 \leq x < 2$ ：E组： $x \geq 2$ ．根据调查结果绘制成两幅不完整的统计图如图所示．请根据图中提供的信息，解答下列问题：

(1)、本次共调查了名学生；

(2)、补全条形统计图；

(3)、在扇形统计图中，求C组所对应的扇形圆心角的度数；

(4)、若该校有1800名学生，请估计该校完成作业的时间少于2小时的学生有多少名．

查看试题解析
25. 小鑫和小许相约去猴石山游玩，小鑫骑自行车，小许骑电动车先后从学校出发沿同一路线匀速骑行，小许在骑行过程中的速度始终保持 $25 km/h$ ．设小鑫骑行的时间为 $x$ （单位： $h$ ），小许、小鑫两人之间的距离 $y$ （单位： $km$ ）关于 $x$ 的函数图象如图所示，请解决以下问题：

(1)、小鑫的速度是 $km/h$ ， $a =$ ， $b =$ ；

(2)、求出小许和小鑫第一次相遇之后，两人之间的距离 $y$ 与小鑫骑行的时间 $x$ 之间的函数关系式，并写出 $x$ 的取值范围；

(3)、请直接写出小许出发多长时间，两人相距 $\frac{15}{2} km$ ．

查看试题解析
26. 在菱形 $A B C D$ 中，点G在直线 $A D$ 上，E为 $B C$ 边的中点， $E F ∥ B G$ 交直线 $A D$ 于点F．

(1)、如图①，求证： $A G - D F = \frac{1}{2} C D$ ；

(2)、如图②、图③，请分别写出线段 $A G ， D F ， C D$ 之间的数量关系，不需要证明．

查看试题解析
27. 为有效预防传染病的传播，学校需购买甲、乙两种消毒液每天对班级进行消杀工作，经了解，每桶甲种消毒液的售价比乙种消毒液的售价多10元，学校用600元和400元采购了相同桶数的甲、乙两种消毒液．

(1)、求甲、乙两种消毒液的售价分别是每桶多少元；

(2)、由于消杀工作的需要，学校需再次购买两种消毒液共500桶，且甲种消毒液的桶数不少于乙种消毒液的桶数，求甲种消毒液购买多少桶时，所需资金总额最少，最少总金额是多少元？

(3)、商家决定对甲、乙两种消毒液打九折销售，在（2）中所需资金总额最少的条件下，学校用节省下来的钱全部购进A，B两种高压喷壶．已知A种高压喷壶50元/个，B种高压喷壶80元/个，请直接写出购进方案．

查看试题解析
28. 如图，将矩形纸片 $O A B C$ 放在平面直角坐标系中，O为坐标原点．点A在y轴上，点C在x轴上， $O A ， O B$ 的长是 $x^{2} - 16 x + 60 = 0$ 的两个根，P是边 $A B$ 上的一点，将 $△ O A P$ 沿 $O P$ 折叠，使点A落在 $O B$ 上的点Q处．

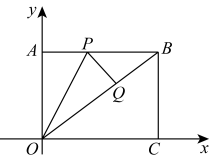(1)、求点B的坐标；

(2)、求直线 $P Q$ 的解析式；

(3)、点M在直线 $O P$ 上，点N在直线 $P Q$ 上，是否存在点M，N，使以A，C．M，N为顶点的四边形是平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．

查看试题解析