黑龙江省大庆市高新区2023年中考一模数学试卷
试卷更新日期:2023-05-25 类型:中考模拟
一、单选题
-
1. 2023的相反数的倒数是( )A、2023 B、 C、 D、2. 大庆市2020年GDP超过了2800亿元,2800亿用科学记数法表示为( )A、2.8×103 B、28×1011 C、2.8×1012 D、2.8×10113. 已知有理数a,b,c在数轴上的对应点的位置如图所示,则下列关系中,正确的( )
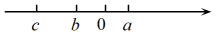 A、 B、 C、 D、4. 地铁标志作为城市地铁的形象和符号,是城市与文化的缩影,下列图案分别为杭州,北京,深圳,上海四个城市的地铁标志,其中是中心对称图形的是( )A、
A、 B、 C、 D、4. 地铁标志作为城市地铁的形象和符号,是城市与文化的缩影,下列图案分别为杭州,北京,深圳,上海四个城市的地铁标志,其中是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 某校要从四名学生中选拔一名参加市“汉字听写”大赛,将多轮选拔赛的成绩数据进行分析得到每名学生的平均成绩及其方差如下表所示:
5. 某校要从四名学生中选拔一名参加市“汉字听写”大赛,将多轮选拔赛的成绩数据进行分析得到每名学生的平均成绩及其方差如下表所示:甲
乙
丙
丁
平均数(单位:分)
m
90
91
88
方差(单位:分2)
n
12.5
14.5
11
根据表中数据,可以判断同学甲是这四名选手中成绩最好且发挥最稳定的学生,则m,n的值可以( )
A、 B、 C、 D、6. 已知一个圆锥的三视图如图所示,则这个圆锥的体积为( )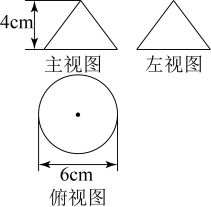 A、 B、 C、 D、7. 如图,在正方形中, , 点E,F分别在边上, , 若将四边形沿折叠,点恰好落在边上,则的长度为( )
A、 B、 C、 D、7. 如图,在正方形中, , 点E,F分别在边上, , 若将四边形沿折叠,点恰好落在边上,则的长度为( ) A、1 B、 C、 D、28. 下列说法正确的是( )A、相等的角是对顶角 B、在同一平面内,不相交的两条直线必平行 C、从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离 D、两条直线被第三条直线所截,同位角相等9. 如图,点和都在反比例函数的图象上,过点A分别向x轴y轴作垂线,垂足分别是M、N,连接、 , 若四边形的面积记作 , 面积记作 , 则( )
A、1 B、 C、 D、28. 下列说法正确的是( )A、相等的角是对顶角 B、在同一平面内,不相交的两条直线必平行 C、从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离 D、两条直线被第三条直线所截,同位角相等9. 如图,点和都在反比例函数的图象上,过点A分别向x轴y轴作垂线,垂足分别是M、N,连接、 , 若四边形的面积记作 , 面积记作 , 则( )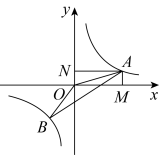 A、 B、 C、 D、10. 如图①,在矩形 中,H为 边上的一点,点M从点A出发沿折线 运动到点B停止,点N从点A出发沿 运动到点B停止,它们的运动速度都是 ,若点M、N同时开始运动,设运动时间为 , 的面积为 ,已知S与t之间函数图象如图②所示,则下列结论正确的是( )
A、 B、 C、 D、10. 如图①,在矩形 中,H为 边上的一点,点M从点A出发沿折线 运动到点B停止,点N从点A出发沿 运动到点B停止,它们的运动速度都是 ,若点M、N同时开始运动,设运动时间为 , 的面积为 ,已知S与t之间函数图象如图②所示,则下列结论正确的是( )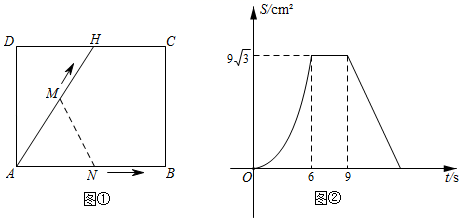
①当 时, 是等边三角形.②在运动过程中,使得 为等腰三角形的点M一共有3个.③当 时, .④当 时, .⑤当 时, .
A、①③④ B、①③⑤ C、①②④ D、③④⑤二、填空题
-
11. 已知一次函数的图象不经过第二象限,则的范围 .12. 黑龙江省第五届旅游发展大会将于2023年夏季在大庆市举办,为“迎旅发”,创建美丽城市,九年级学生设计了正方体废纸回收盒,如图所示,将写有“庆”字的正方形添加到图中,使它们构成完整的正方体展开图,共有 种添加方式.
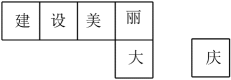 13. 数学家发明了一个魔术盒,当任意实数对进入其中时,会得到一个新的实数: . 例如把放入其中,就会得到 . 现将实数对放入其中得到实数m,再将实数对放入其中后,得到的实数是 .14. 若关于x的不等式只有3个正整数解,则m的取值范围是 .15. 哈齐高铁于2015年开通,是我国目前最北端的高速铁路,开通8年时间,方便了千千万万大庆市民出行,也推动了龙江经济发展.从大庆西站到哈尔滨站中间有4个车站,共有 种票价.(注:拟设每两个城市之间的票价相同)16. 如图,点 , , , , …….根据这个规律,探究可得点的坐标是 .
13. 数学家发明了一个魔术盒,当任意实数对进入其中时,会得到一个新的实数: . 例如把放入其中,就会得到 . 现将实数对放入其中得到实数m,再将实数对放入其中后,得到的实数是 .14. 若关于x的不等式只有3个正整数解,则m的取值范围是 .15. 哈齐高铁于2015年开通,是我国目前最北端的高速铁路,开通8年时间,方便了千千万万大庆市民出行,也推动了龙江经济发展.从大庆西站到哈尔滨站中间有4个车站,共有 种票价.(注:拟设每两个城市之间的票价相同)16. 如图,点 , , , , …….根据这个规律,探究可得点的坐标是 .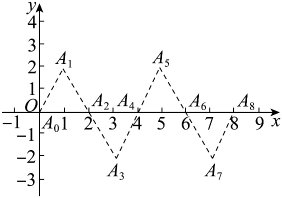 17. 如图, , 是的两条弦,且 , 点D,P分别在 , 上,若 , 则的度数为 .
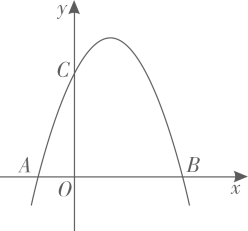
17. 如图, , 是的两条弦,且 , 点D,P分别在 , 上,若 , 则的度数为 .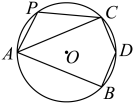 18. 已知抛物线(a,b,c是常数,),且 , . 下列四个结论:
18. 已知抛物线(a,b,c是常数,),且 , . 下列四个结论:①对于任意实数 , 恒成立;
②若 , 则不等式的解集是;
③一元二次方程有一个根;
④点 , 在抛物线上,若 , 则当时,总有 . 其中正确的是 . (填写序号)
三、解答题
-
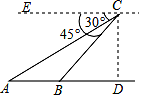
19.(1)、计算:;(2)、化简: .20. 先化简: , 再从0, , , 2中选择一个合适的数作为x的值代入求值.21. 现需加工一批物件,甲单独做4天完成,乙单独做6天完成.现由乙先做1天,再两人合作,完成后共得报酬500元,如果按每人工作量分配报酬,那么该如何分配?22. 阳春三月,春暖花开,莲花山风景区游人如织,某摄影爱好者正在用无人机进行航拍.如图,在无人机镜头C处,观测风景区A处的俯角为30°,B处的俯角为45°,已知A,B两点之间的距离为200米,则无人机镜头C处的高度CD为多少?(点A,B,D在同一条直线上,结果保留根号)
 23. 教育部办公厅在《关于进一步加强中小学生体质健康管理工作的通知》中明确要求保障学生每天校内、校外各1小时体育活动时间.某校为了解本校九年级学生每天参加体育活动的情况,随机抽取了名学生,对某一天的体育活动时间进行了调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图.
23. 教育部办公厅在《关于进一步加强中小学生体质健康管理工作的通知》中明确要求保障学生每天校内、校外各1小时体育活动时间.某校为了解本校九年级学生每天参加体育活动的情况,随机抽取了名学生,对某一天的体育活动时间进行了调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图.调查结果的频数分布表
组别
时间(分钟)
频数
5
12
8
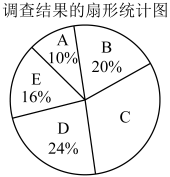
根据上述信息,解答下列问题:
(1)、频数分布表中的 , 扇形统计图中组所在的扇形的圆心角为度;(2)、被抽取的名学生这一天的体育活动时间数据的中位数在哪一组(直接写出组别即可);(3)、若该校九年级共有720名学生,试估计该校九年级学生平均每天体育活动时间不低于120分钟的学生人数.24. 如图,在中,E为的中点,延长 , 交于点F,连接 , .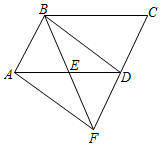 (1)、求证:;(2)、若 , , , 求的长.25. 大庆市为了筹建第五届旅发大会,建设滨水绿道,围绕“以河连湖,以绿串蓝”的理念,秉承“惠及民生、全民共享”的初心,串起一河五湖,沿黎明河主轴线纵伸延展,采用上跨立交和下穿通行的方式,建成一个全长公里的滨水生态慢行系统.小东与父亲每天在某区段匀速慢跑,以距离为一个训练段.已知父子俩起点终点均相同,约定先到终点的人原地休息等待另一人.已知小东先出发 , 如图,两人之间的距离与父亲出发的时间之间的函数关系如图所示.请回答下列问题:
(1)、求证:;(2)、若 , , , 求的长.25. 大庆市为了筹建第五届旅发大会,建设滨水绿道,围绕“以河连湖,以绿串蓝”的理念,秉承“惠及民生、全民共享”的初心,串起一河五湖,沿黎明河主轴线纵伸延展,采用上跨立交和下穿通行的方式,建成一个全长公里的滨水生态慢行系统.小东与父亲每天在某区段匀速慢跑,以距离为一个训练段.已知父子俩起点终点均相同,约定先到终点的人原地休息等待另一人.已知小东先出发 , 如图,两人之间的距离与父亲出发的时间之间的函数关系如图所示.请回答下列问题: (1)、小东的速度为、父亲的速度为;(2)、求出点坐标和所在直线的解析式;(3)、直接写出整个过程中,哪个时间段内,父子两人之间距离超过了 .26. 如图,已知一次函数的图象与反比例函数第一象限内的图象相交于点 , 与x轴相交于点B.
(1)、小东的速度为、父亲的速度为;(2)、求出点坐标和所在直线的解析式;(3)、直接写出整个过程中,哪个时间段内,父子两人之间距离超过了 .26. 如图,已知一次函数的图象与反比例函数第一象限内的图象相交于点 , 与x轴相交于点B.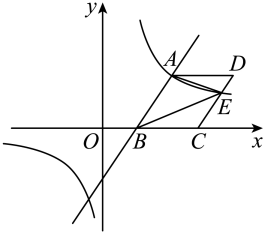 (1)、求n和k的值;(2)、如图,以为边作菱形 , 使点C在x轴正半轴上,点D在第一象限,双曲线交于点E,连接 , 求 .
(1)、求n和k的值;(2)、如图,以为边作菱形 , 使点C在x轴正半轴上,点D在第一象限,双曲线交于点E,连接 , 求 .