黑龙江省齐齐哈尔市2023年中考一模数学试卷
试卷更新日期:2023-05-24 类型:中考模拟
一、单选题
-
1. 实数﹣2023的绝对值是( )A、2023 B、﹣2023 C、 D、2. 王老师给全班同学留了一个特色寒假作业,画一张有关兔子的图画,以下四个图形是开学后收上来的图画中的一部分,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 将一副直角三角尺,按如图所示位置摆放,使角所对的直角边和含角的三角尺的直角边放在同一条直线上,则的度数是( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 将一副直角三角尺,按如图所示位置摆放,使角所对的直角边和含角的三角尺的直角边放在同一条直线上,则的度数是( ) A、 B、 C、 D、5. 如图,由6个同样大小的正方体摆成的几何体,在正方体①的正上方再放一个这样的正方体,所得的几何体( )
A、 B、 C、 D、5. 如图,由6个同样大小的正方体摆成的几何体,在正方体①的正上方再放一个这样的正方体,所得的几何体( )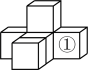 A、主视图改变,左视图不变 B、俯视图改变,左视图不变 C、俯视图改变,左视图改变 D、主视图改变,左视图改变6. 若关于的方程的解为非负数,则的取值范围是( )A、 B、且 C、 D、且7. 甲、乙、丙三人参加班级举行的“我爱家乡”演讲比赛,需要通过抽签方式来决定出场顺序,则出场顺序恰好是甲、乙、丙的概率是( )A、 B、 C、 D、8. 如图,在中, , , 点分别从点和点同时出发,以相同的速度沿射线向左匀速运动,过点作 , 垂足为 , 连接 , 设点运动的距离为 , 的面积为 , 则能反映与之间的函数关系的图象大致为( )
A、主视图改变,左视图不变 B、俯视图改变,左视图不变 C、俯视图改变,左视图改变 D、主视图改变,左视图改变6. 若关于的方程的解为非负数,则的取值范围是( )A、 B、且 C、 D、且7. 甲、乙、丙三人参加班级举行的“我爱家乡”演讲比赛,需要通过抽签方式来决定出场顺序,则出场顺序恰好是甲、乙、丙的概率是( )A、 B、 C、 D、8. 如图,在中, , , 点分别从点和点同时出发,以相同的速度沿射线向左匀速运动,过点作 , 垂足为 , 连接 , 设点运动的距离为 , 的面积为 , 则能反映与之间的函数关系的图象大致为( )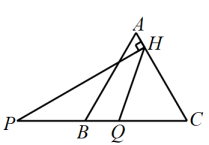 A、
A、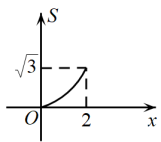 B、
B、 C、
C、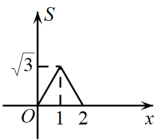 D、
D、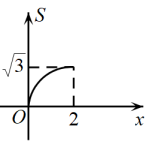 9. 2022年9月,某校学生会以“心连心向未来”为主题,举办了庆祝香地回归25周年征文活动,选派20名学生会成员对120篇征文进行分类 ,现将20名学生会成员分为三组,若第一、二、三小组每人分别负责8 、6、5篇征文,且每组至少有2人,则学生会成员分组方案有( )A、4种 B、5种 C、8种 D、9种10. 如图,抛物线 , 与轴正半轴交于两点, 与轴负半轴交于点 .
9. 2022年9月,某校学生会以“心连心向未来”为主题,举办了庆祝香地回归25周年征文活动,选派20名学生会成员对120篇征文进行分类 ,现将20名学生会成员分为三组,若第一、二、三小组每人分别负责8 、6、5篇征文,且每组至少有2人,则学生会成员分组方案有( )A、4种 B、5种 C、8种 D、9种10. 如图,抛物线 , 与轴正半轴交于两点, 与轴负半轴交于点 .①;
②;
③若点的坐标为 , 且 , 则;
④若抛物线的对称轴是直线 , 为任意实数;
则 .
上述结论中,正确的个数是( )
 A、0个 B、1个 C、2个 D、3个
A、0个 B、1个 C、2个 D、3个二、填空题
-
11. 2022年2月5日,在北京冬奥会短道速滑混合团体2000米接力决赛中,由武大靖、任子威、曲春雨、范可新和张雨婷组成的中国队获得金牌,也是中国代表团该届冬奥会的首枚金牌.取得这样骄人成绩的背后是运动健儿们日复一日的艰苦训练,请你计算一下,如果武大靖每天速滑训练1万米,用科学记数法表示365天共速滑训练米.12. 如图,正方形中,点分别在上,连接 , 请添加一个条件: , 使 .
 13. 在函数 中,自变量x的取值范围是 .14. 要制作一个高为8cm,底面圆直径是12cm的圆锥形小漏斗,若不计接缝,不计损耗,则她所需纸板的面积是cm2 .15. 如图,在平面直角坐标系中菱形的顶点的坐标为 , 且 , 点在第一象限,连接对角线 , 函数的图象分别交于点 , 若 , 则 .
13. 在函数 中,自变量x的取值范围是 .14. 要制作一个高为8cm,底面圆直径是12cm的圆锥形小漏斗,若不计接缝,不计损耗,则她所需纸板的面积是cm2 .15. 如图,在平面直角坐标系中菱形的顶点的坐标为 , 且 , 点在第一象限,连接对角线 , 函数的图象分别交于点 , 若 , 则 . 16. 矩形的边 . 点为平面内一点, , 若 , 则 .17. 如图,正方形的中心与坐标原点O重合,将顶点绕点逆时针旋转得点 , 再将绕点逆时针旋转得点 , 再将绕点C逆时针旋转得点 , 再将绕点D逆时针旋转得点 , 再将绕点A逆时针旋转得点……依此类推,则点的坐标是.
16. 矩形的边 . 点为平面内一点, , 若 , 则 .17. 如图,正方形的中心与坐标原点O重合,将顶点绕点逆时针旋转得点 , 再将绕点逆时针旋转得点 , 再将绕点C逆时针旋转得点 , 再将绕点D逆时针旋转得点 , 再将绕点A逆时针旋转得点……依此类推,则点的坐标是.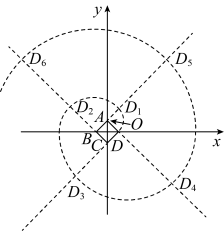
三、解答题
-
18.(1)、计算:(2)、分解因式:19. 解方程20. 某校为了解七、八年级学生对“疫情防护”安全知识的掌握情况,从七、八年级各随机抽出50名学生进行测试,并对成绩(百分制)进行整理、描述和分析,部分信息如下:
七、八年级成绩平均数、中位数如下表:
年级
平均数
中位数
七年级
76.8
八年级
79.2
79.5
七年级成绩频数分布直方图如下图:
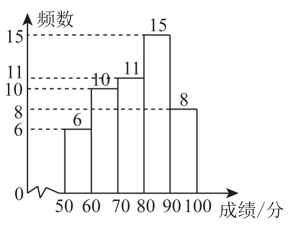
七年级成绩在这一组的数据如下表:
70
72
74
75
76
76
77
77
77
78
79
根据以上信息,解答下列问题:
(1)、在这次测试中,七年级学生成绩在80分以上(含80分)的有人;(2)、表中的值为;(3)、在这次测试中,七年级学生甲和八年级学生乙的成绩都是78分,则甲、乙两位学生在各自年级的排名更靠前(按照分数由高到低的顺序排名);(4)、该校七年级学生有700人,请估计七年级学生成绩不低于80分的有多少人?21. 如图,内接于 , 延长直径到 , 使 , 过圆心作的平行线交的延长线于点 . (1)、求证:是的切线;(2)、若 , 求的半径及 .22. 某实验室对甲、乙两机器人进行装卸货物测试,在实验场地的一条直线上依次设置货物装卸点三地,甲、乙两机器人同时从地匀速出发,甲机器人到达地后装货1分钟,再以原速原路返回地,乙机器人到达地后装货1分钟,再以原速前往地,结果甲、乙两机器人同时到达各自目的地,在两机器人行驶的过程中,甲、乙两机器人距地的距离(单位:米)与甲机器人所用时间(单位:分)之间的函数图象如图所示,请结合图像信息解答下列问题:
(1)、求证:是的切线;(2)、若 , 求的半径及 .22. 某实验室对甲、乙两机器人进行装卸货物测试,在实验场地的一条直线上依次设置货物装卸点三地,甲、乙两机器人同时从地匀速出发,甲机器人到达地后装货1分钟,再以原速原路返回地,乙机器人到达地后装货1分钟,再以原速前往地,结果甲、乙两机器人同时到达各自目的地,在两机器人行驶的过程中,甲、乙两机器人距地的距离(单位:米)与甲机器人所用时间(单位:分)之间的函数图象如图所示,请结合图像信息解答下列问题: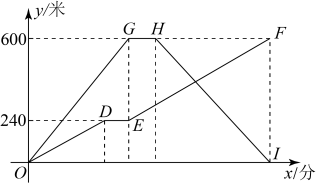 (1)、 两地之间的距离为米,甲机器人的速度为米/分;(2)、求乙机器人从地到地行驶过程中与的函数关系式(不用写出的取值范围);(3)、两机器人经过多长时间相距120米?请直接写出答案.23. 综合与实践
(1)、 两地之间的距离为米,甲机器人的速度为米/分;(2)、求乙机器人从地到地行驶过程中与的函数关系式(不用写出的取值范围);(3)、两机器人经过多长时间相距120米?请直接写出答案.23. 综合与实践旋转是几何图形运动中的一种重要变换,通常与全等三角形等数学知识相结合来解决实际问题,某学校数学兴趣小组在研究三角形旋转的过程中,进行如下探究:如图1,和均为等腰直角三角形, , 点为中点,绕点旋转,连接 .

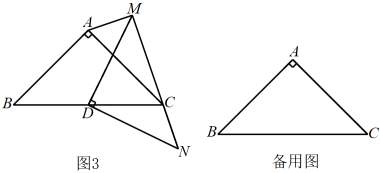
观察猜想
(1)、在旋转过程中,与的数量关系为;(2)、实践发现
当点在内且三点共线时,如图2,求证:;(3)、当点在外且三点共线时,如图3,探究之间的数量关系是;(4)、若中, , 在旋转过程中,当且三点共线时, .24. 综合与探究如图,在平面直角坐标系中,直线与轴交于点,与轴交于点,抛物线)经过 , 两点,与轴相交于另一点 , 连接 . 点是线段上方抛物线上的一个动点,过点作交线段于点 .
 (1)、求抛物线的解析式;(2)、点为抛物线对称轴上的一个动点,则的最大值是;(3)、求的最大值,并写出此时点的坐标;(4)、在轴上找一点 , 抛物线上找一点 , 使以点为顶点的四边形是平行四边形,请直接写出点的坐标.
(1)、求抛物线的解析式;(2)、点为抛物线对称轴上的一个动点,则的最大值是;(3)、求的最大值,并写出此时点的坐标;(4)、在轴上找一点 , 抛物线上找一点 , 使以点为顶点的四边形是平行四边形,请直接写出点的坐标.