浙江省舟山市金衢山五校联考2022学年八年级下学期期中素养监测数学试题卷

试卷更新日期：2023-05-24 类型：期中考试

进入出卷网下载

一、造择题：(本大题共10个小题，每小题3分，共30分)

1. 以下是回收、节水、绿色包装、低碳4个标志，其中是中心对称图形的是（）。

A、 B、 C、 D、

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{(- 2)_{}^{2}} = - 2$ C、 $2 \sqrt{2} - \sqrt{2} = 2$ D、 $\sqrt{2} \times \sqrt{8} = 4$

查看试题解析
3. 一个n边形的各内角都等于 $120 °$ ，则n等于（）

A、5 B、6 C、7 D、8

查看试题解析
4. 用配方法将方程 $x_{}^{2} - 4 x - 4 = 0$ 化成 $(x + m)_{}^{2} = n$ 的形式，则 $m ， n$ 的值是（）

A、-2，0 B、2，0 C、-2，8 D、2，8

查看试题解析
5. 为了解某校同学参加社团的情况，抽查了100名同学统计他们在一周中参加社团活动的时间，绘成如图所示的频数分布直方图，参加社团活动时间的中位数所在范围是（）

A、2-3小时 B、3-4小时 C、4-5小时 D、5-6小时

查看试题解析
6. 如图，已知点A，B的坐标分别是(1，1)，(-2，-1)，四边形ABCD 是平行四边形，点D 的坐标是(4，1)，则点C 的坐标为（）

A、(2，- 1) B、(2，1) C、(-2，3) D、(1，- 1)

查看试题解析
7. 用反证法证明命题“一个三角形中至多有一个角是直角”，应先假设这个三角形中（）．

A、至少有两个角是直角　　　　 B、没有直角 C、至少有一个角是直角　　　　 D、有一个角是钝角，一个角是直角

查看试题解析
8. 如图，平行四边形ABCD中，O为对角线交点， DP平分∠ADC，CP 平分∠BCD，AB=7， AD=10，则 OP的长为（） .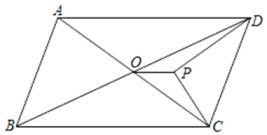

A、1.5 B、2 C、2.5 D、3

查看试题解析
9. 为了宣传环保，某学生写了一份倡议书在微博传播，规则为：将倡议书发表在自己的微博，再邀请n个好友转发倡议书，每个好友转发倡议书，又邀请n个互不相同的好友转发倡议书，以此类推，已知经过两轮传播后，共有1641人参与了传播活动，则方程列为（）

A、(n+1)²=1641 B、(n- 1)²=1641 C、n(n+1)=1641 D、1+n+n²=1641

查看试题解析
10. 对于一元二次方程 $a x_{}^{2} + b x + c = 0$ (a≠0)，有下列说法：
①若方程 $a x_{}^{2} + c = 0$ 有两个不相等的实数根，则方程 $a x_{}^{2} + b x + c = 0$ (a≠0) 必有两个不相等的实数根；②若方程 $a x_{}^{2} + b x + c = 0$ (a≠0)有两个实数根，则方程 $c x_{}^{2} + b x + a = 0$ 一定有两个实数根；③若c是方程 $a x_{}^{2} + b x + c = 0$ (a≠0)的一个根，则一定有ac+b+1=0 成立；④若 $x_{0}^{}$ 是一元二次方程 $a x_{}^{2} + b x + c = 0$ (a≠0)的根，则 $b_{}^{2} - 4 a c = (2 a x_{0}^{} - b)_{}^{2}$

其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题：(本大题共6个小题，每小题4分，共24分)

11. 当 $x = 1$ 时，二次根式 $\sqrt{x + 3}$ 的值为．

查看试题解析
12. 甲、乙两个篮球队队员身高的平均数都为2.07米，若方差 $S_{甲}^{2} < S_{乙}^{2}$ ，则队员身高比较整齐的球队是队(填“甲”或“乙”).

查看试题解析
13. 一元二次方程 $x^{2} - 4 x + 2 = 0$ 的两根为 $x_{1}$ , $x_{2}$ ,则 $x_{1}^{2} - 4 x_{1} + 2 x_{1} x_{2}$ 的值为 .

查看试题解析
14. 在实数范围内，存在2个不同的x 的值，使代数式 $x_{}^{2} - 3 x + c$ 与代数式 $x + 2$ 值相等，则c的取值范围是.

查看试题解析
15. 如图，在长方形ABCD中，AE ⊥BD于点E，CF ⊥BD于点F，连接 CE，AF

(1)、若AD：AB= $\sqrt{2}$ ：1，则四边形ABCF与长方形ABCD的面积之比为，；

(2)、若AD：AB= $\sqrt{a}$ ：1，则四边形AECF与长方形ABCD的面积之比为

查看试题解析
16. 如图，有一张平行四边形纸条 ABCD，AD=5cm，AB=2cm， ∠A=120°，点E，F 分别在边 AD，BC上，DE=1cm. 现将四边形 CFED沿EF折叠，使点C，D 分别落在点C’，D '上.当点C’恰好落在边AD上时，线段 CF的长为cm .在点F 从点B 运动到点C的过程中，若边 $F C'$ 与边AD交于点M，则点M相应运动的路径长为cm.

查看试题解析

三、解答题：(本大题共8个小题，66分)

17. 计算

(1)、 $\sqrt{8} - \sqrt{\frac{1}{2}} + \sqrt{18}$ ，

(2)、 $(\sqrt{2} + \sqrt{3})_{}^{2} - \sqrt{24}$

查看试题解析
18. 解下列方程：

(1)、 $x (x + 1) = (x + 1)$

(2)、 $2 x_{}^{_{2}^{}} - 3 x - 1 = 0$

查看试题解析
19. 如图所示.
① ②

(1)、请你在图①中画出△ $A' B' C'$ ，使其与△ABC关于点O成中心对称；

(2)、请你在图②中△ABC的边上找一个点M，作出△DEF，使其与△ABC关于点M成中心对称，使△DBF与△ABC合成的图形为平行四边形.

查看试题解析
20. 比较 $- \frac{1}{2} x_{}^{2} + 2 x$ 与 $- x + 5$ 的大小.

(1)、尝试(用“<”， “=”或“>”填空)：
①当x=1 时， $- \frac{1}{2} x_{}^{2} + 2 x$ $- x + 5$
②当x=0 时， $- \frac{1}{2} x_{}^{2} + 2 x$ $- x + 5$
③当 x=-2 时， $- \frac{1}{2} x_{}^{2} + 2 x$ $- x + 5$

(2)、归纳：若x 取任意实数， $- \frac{1}{2} x_{}^{2} + 2 x$ 与 $- x + 5$ 有怎样的大小关系?试说明理由.

查看试题解析
21. 为了解甲、乙两座城市的邮政企业4月份收入的情况，从这两座城市的邮政企业中，各随机抽取了25家邮政企业，获得了它们4月份收入(单位：百万元)的数据，并对数据进行整理、描述和分析.下面给出了部分信息：
a. 甲城市邮政企业4月份收入的数据的频数分布直方图如图(数据分成5组：6≤x<8，8≤x<10，10≤x<12，12≤x<14，14≤x≤16)；

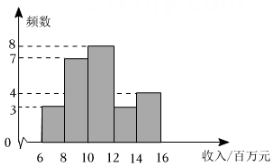
b. 甲城市邮政企业4月份收入的数据在10≤x<12 这一组的是：10.0 10.0 10.1 10.9 11.4 11.5 11.6 11.8；
c. 甲、乙两座城市邮政企业4月份收入的数据的平均数、中位数如表：

平均数

中位数

甲城市

10.8

m

乙城市

11.0

11.5

根据以上信息，回答下列问题：

(1)、写出表中m 的值；

(2)、在甲城市抽取的邮政企业中，记4月份收入高于它们的平均收入的邮政企业的个数为 p₁. 在乙城市抽取的邮政企业中，记4 月份收入高于它们的平均收入的邮政企业的个数为p₂. 比较p₁ ， p₂ 的大小，并说明理由；

(3)、若乙城市共有200家邮政企业，估计乙城市的邮政企业4月份的总收入（直接写出结果）.

查看试题解析
22. 如图，在平行四边形ABCD中，E为BC边上一点，且AB=AE.

(1)、求证：△ABC≌△EAD；

(2)、若AE平分∠DAB，∠EAC=30°，BE=2 $\sqrt{3}$ 求∠AED的度数及平行四边形ABCD 的面积.

查看试题解析
23. 某商店将A、B两种巧克力进行降价促销活动，经统计，某一天前来购买这两种巧克力的顾客共有480名，每名顾客均购买了一盒巧克力，其中A、B两种巧克力的销售单价分别为90元和50元.

(1)、若选择购买B种巧克力的人数不超过购买A 种巧克力人数的0.6倍，求至少有多少人选择购买A 种巧克力?

(2)、3月8日是女神节，该商店估计当天购买巧克力的人会比较多，于是提高了A 种巧克力的售价，结果发现女神节当天前来购买巧克力的顾客人数出现了下降，经统计发现与(1)问中选择A 种巧克力的人数最少时相比， A种巧克力每上涨3元，购买A种巧克力的人数会下降5人，同时购买B 种巧克力的人数也下降3人，但是B 种巧克力的售价没变，最终女神节期间两种巧克力的总销售额与(1)问中选择A 种巧克力的顾客最少时的两种巧克力的总销售额持平，求女神节当天A种巧克力的售价.

查看试题解析
24. 已知在平行四边形ABCD中，E 是边AD 的中点，F 是边AB上一动点.

(1)、如图1，连接FE并延长交CD的延长线于点G，求证：E 是FG 的中点；

(2)、如图2，若CF⊥AB，AD=2AB，求证：∠DEF=3∠AFE；

(3)、如图3，若CF⊥AB，AD=2AB=4，∠B=60°时，K 是射线CD上一个动点，将EK 逆时针旋转90°得到EM，连接FM，求FM 的最小值。

查看试题解析

	平均数	中位数
甲城市	10.8	m
乙城市	11.0	11.5