浙江省金华市东阳市横店教育联盟2022-2023学年七年级下学期期中数学试卷
试卷更新日期:2023-05-24 类型:期中考试
一、选择题(本大题共10小题,共30.0分。)
-
1. 下列四个图形中,不能通过其中一个四边形平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 2. 2019年12月,新型冠状病毒肺炎爆发,目前检测出的新型冠状病毒的半径平均在50纳米左右,即0.00000005米,用科学记数法表示0.00000005正确的是( )A、 B、 C、 D、3. 下列等式从左到右的变形中,属于因式分解的是( )A、 B、 C、 D、4. 下列各式中,是关于 , 的二元一次方程的是( )A、 B、 C、 D、5. 如图2,烧杯内液体表面与烧杯下底部平行,光线从液体中射向空气时发生折射,光线变成 , 点在射线上已知 , , 则( )
2. 2019年12月,新型冠状病毒肺炎爆发,目前检测出的新型冠状病毒的半径平均在50纳米左右,即0.00000005米,用科学记数法表示0.00000005正确的是( )A、 B、 C、 D、3. 下列等式从左到右的变形中,属于因式分解的是( )A、 B、 C、 D、4. 下列各式中,是关于 , 的二元一次方程的是( )A、 B、 C、 D、5. 如图2,烧杯内液体表面与烧杯下底部平行,光线从液体中射向空气时发生折射,光线变成 , 点在射线上已知 , , 则( ) A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 把多项式分解因式,应提取的公因式是( )A、 B、 C、 D、8. 我国古代数学名著张邱建算经中记载:“今有清酒一斗直粟十斗,醑酒一斗直粟三斗今持粟三斛,得酒五斗,问清、醑酒各几何?意思是:现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清、醑酒各几斗?如果设清酒斗,醑酒斗,那么可列方程组为( )A、 B、 C、 D、9. 已知 , 则( )A、 B、 C、 D、10. 如图,在中, , 按如图所示进行翻折,使 , , 则的度数是( )
A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 把多项式分解因式,应提取的公因式是( )A、 B、 C、 D、8. 我国古代数学名著张邱建算经中记载:“今有清酒一斗直粟十斗,醑酒一斗直粟三斗今持粟三斛,得酒五斗,问清、醑酒各几何?意思是:现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清、醑酒各几斗?如果设清酒斗,醑酒斗,那么可列方程组为( )A、 B、 C、 D、9. 已知 , 则( )A、 B、 C、 D、10. 如图,在中, , 按如图所示进行翻折,使 , , 则的度数是( )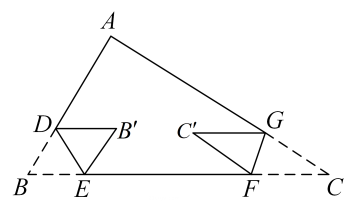 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共24.0分)
-
11. 计算的结果等于 .12. , , 则.13. 如图,把沿方向平移得到 , 则的长是.
 14. 已知方程组与有相同的解,则 , .15. 线段和线段交于点 , 平分 , 点为线段上一点不与点和点重合 , 过点作 , 交线段于点 , 若则的度数为 .
14. 已知方程组与有相同的解,则 , .15. 线段和线段交于点 , 平分 , 点为线段上一点不与点和点重合 , 过点作 , 交线段于点 , 若则的度数为 .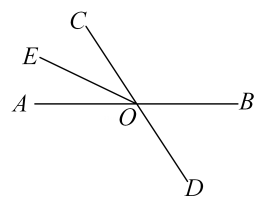 16. 如图,长方形中放入一个边长为的大正方形和两个边长为6的小正方形及正方形 .
16. 如图,长方形中放入一个边长为的大正方形和两个边长为6的小正方形及正方形 . (1)、若阴影部分与为正方形,且的面积为1,则 .(2)、若3个阴影部分的面积满足 , 则长方形的面积为 .
(1)、若阴影部分与为正方形,且的面积为1,则 .(2)、若3个阴影部分的面积满足 , 则长方形的面积为 .三、解答题(本大题共8小题,共66.0分。)
-
17. 计算:(1)、 .(2)、用简便方法计算18.(1)、解方程组:;(2)、先化简后求值: , 其中 .19. 已知如图.
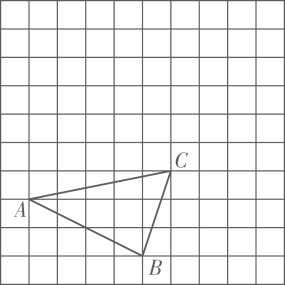 (1)、求的面积;(2)、将向上平移4个单位,再向右平移4个单位得到 , 画出平移后的图形.20. 把下面的说理过程补充完整.
(1)、求的面积;(2)、将向上平移4个单位,再向右平移4个单位得到 , 画出平移后的图形.20. 把下面的说理过程补充完整.已知:如图, , , 试判断与的关系,并说明理由.

解:
平角定义 , 已知
已知 ▲ ( )
21. 在疫情防控期间,某中学为保障广大师生生命健康安全,欲从商场购进一批免洗手消毒液和84消毒液.已知如下购买情况:免洗手消毒液
84消毒液
总花费
第一次购买
40瓶
90瓶
1320
第二次购买
60瓶
120瓶
1860
(1)、求每瓶免洗手消毒液和每瓶84消毒液的价格分别是多少元?(2)、若商场有两种促销方案:方案一:所有购买商品均打九折;
方案二:每购买5瓶免洗手消毒液送2瓶84消毒液;
学校打算购进免洗手消毒液100瓶,84消毒液60瓶,请问学校选用哪种方案更省钱?省多少钱?
22. 如图1是一个长为、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2)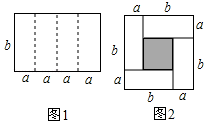 (1)、观察图2请你写出、、之间的等量关系是;(2)、根据(1)中的结论,若 , 则;(3)、拓展应用:若 , 求的值.23. 我们学过单项式除以单项式、多项式除以单项式,那么多项式除以多项式该怎么计算呢?我们也可以用竖式进行类似演算,即先把被除式、除式按某个字母的指数从大到小依次排列项的顺序,并把所缺的次数项用零补齐,再类似数的竖式除法求出商式和余式,其中余式为0或余式的次数低于除式的次数.
(1)、观察图2请你写出、、之间的等量关系是;(2)、根据(1)中的结论,若 , 则;(3)、拓展应用:若 , 求的值.23. 我们学过单项式除以单项式、多项式除以单项式,那么多项式除以多项式该怎么计算呢?我们也可以用竖式进行类似演算,即先把被除式、除式按某个字母的指数从大到小依次排列项的顺序,并把所缺的次数项用零补齐,再类似数的竖式除法求出商式和余式,其中余式为0或余式的次数低于除式的次数.例:计算, , 可依照的计算方法用竖式进行计算因此 .
 (1)、的商是 .(2)、已知一个长为 , 宽为的长方形 , 若将它的长增加6,宽增加就得到一个新长方形 , 此时长方形的周长是周长的2倍如图 , 用含的代数式表示 .(3)、在(2)的条件下,另有长方形的一边长为 , 若长方形的面积比的面积大76,求长方形的另一边长.24. 如图1,已知 , 是直线 , 外的一点, 于点 , 交 于点 ,满足 .
(1)、的商是 .(2)、已知一个长为 , 宽为的长方形 , 若将它的长增加6,宽增加就得到一个新长方形 , 此时长方形的周长是周长的2倍如图 , 用含的代数式表示 .(3)、在(2)的条件下,另有长方形的一边长为 , 若长方形的面积比的面积大76,求长方形的另一边长.24. 如图1,已知 , 是直线 , 外的一点, 于点 , 交 于点 ,满足 .
 (1)、求 的度数;(2)、如图2,射线 从 出发,以每秒 的速度绕 点按逆时针方向匀速旋转,当 到达 时立刻返回至 ,然后继续按上述方式旋转;射线 从 出发,以相同的速度绕 点按顺时针方向旋转至 后停止运动,此时射线 也停止运动.若射线 、射线 同时开始运动,设运动时间为 秒.
(1)、求 的度数;(2)、如图2,射线 从 出发,以每秒 的速度绕 点按逆时针方向匀速旋转,当 到达 时立刻返回至 ,然后继续按上述方式旋转;射线 从 出发,以相同的速度绕 点按顺时针方向旋转至 后停止运动,此时射线 也停止运动.若射线 、射线 同时开始运动,设运动时间为 秒.①当射线 平分 时,求 的度数 ;
②当直线 与直线 相交所成的锐角是 时,则 __▲__.