浙江省温州市龙湾区部分校2022-2023学年八年级下学期期中数学试卷

试卷更新日期：2023-05-24 类型：期中考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分．）

1. 下列方程是一元二次方程的是（）

A、 $x^{2} + \frac{1}{x} = 3$ B、x²+xy-5＝0 C、x²+2x＝3 D、x+3（x-1）＝5x

查看试题解析
2. 若 $\sqrt{x - 3}$ 在实数范围内有意义，则x的取值范围是（）

A、x＞0 B、x＞3 C、x≥0 D、x≥3

查看试题解析
3. 已知x＝1是一元二次方程x²+ax+2＝0的一个根，则a的值为（）

A、-3 B、-2 C、2 D、3

查看试题解析
4. 下列二次根式中，属于最简二次根式的是（）

A、 $\sqrt{9}$ B、 $\sqrt{3}$ C、 $\sqrt{\frac{1}{2}}$ D、 $\frac{2}{\sqrt{5}}$

查看试题解析
5. 五边形的内角和为（）

A、360° B、540° C、720° D、900°

查看试题解析
6. 为调查某班学生每天使用零花钱的情况，小丽随机调查了20名同学，结果如表：

每天使用零花钱（单位：元）

10

15

20

25

30

人数

1

3

6

5

5

则这20名同学每天使用的零花钱的众数是（）

A、10 B、15 C、20 D、30

查看试题解析
7. 用配方法解方程x²-4x-3＝0，下列配方正确的是（）

A、（x+2）²＝3 B、（x+2）²＝7 C、（x-2）²＝3 D、（x-2）²＝7

查看试题解析
8. 图1是第七届国际数学教育大会（ICME）的会徽，主体图案是由如图2的一连串直角三角形演化而成，其中OA₁＝A₁A₂＝A₂A₃＝…＝A₇A₈＝a．若OA₈＝8，则a的值为（）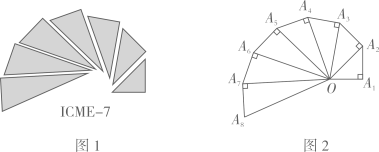

A、2 $\sqrt{2}$ B、2 C、 $\sqrt{2}$ D、1

查看试题解析
9. 某药店一月份销售口罩500包，一至三月份共销售口罩1820包，设该店二、三月份销售口罩的月平均增长率为x，则根据题意可列出方程为（）

A、500（1+x）²＝1820 B、500+500（1+x）+500（1+x）²＝1820 C、500（1+2x）＝1820 D、500+500（1+x）+500（1+2x）＝1820

查看试题解析
10. 勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载．如图1，在△ABC中，∠C＝90°，以△ABC的各边为边分别向外作正方形，再把较小的两个正方形按如图2所示放置，连结MG，DG．若MG⊥DG，AF＝1，则△ABC的面积为（）

A、6 B、 $4 \sqrt{3}$ C、8 D、 $4 \sqrt{5}$

查看试题解析

二、填空题（本题有8小题，每小题3分，共24分）

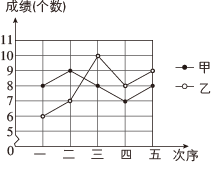
11. 当x＝3时，则 $\sqrt{6 + x}$ 的结果是．

查看试题解析
12. 甲、乙两名同学本学期五次引体向上的测试成绩（个数）如图所示，若甲，乙五次成绩的方差分别为 $S_{甲}^{2}$ ， $S_{乙}^{2}$ ，则 $S_{甲}^{2}$ $S_{乙}^{2}$ （填“＞，＜，＝”）

查看试题解析
13. 如图，在▱ABCD中，P是AD边上一点．已知S_△ABP＝2.5cm² ， S_△CDP＝1.5cm² ，则▱ABCD的面积是 cm² ．

查看试题解析
14. 关于x的方程x²-8x+m＝0有两个相等的实数根，则m的值是．

查看试题解析
15. 在一次演讲比赛中，某位选手的演讲内容、演讲表达的得分分别为90分，85分，将演讲内容、演讲表达的成绩按6：4计算，则该选手的成绩是分．

查看试题解析
16. 如图，在▱ABCD中，∠B＝75°，AC＝AD，则∠DAC的度数是 °．

查看试题解析
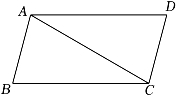17. 如图所示，某市世纪广场有一块长方形绿地长18m，宽15m，在绿地中开辟三条道路后，剩余绿地的面积为224m² ，则图中x的值为．

查看试题解析
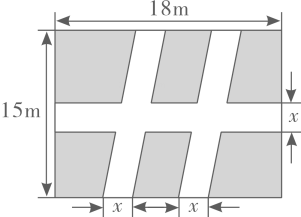18. 如图2，是某款台灯（图1）的示意图，处于水平位置的横杆EF可以绕着点O转动．当OF分别转到OM，ON的位置时，测得∠MON＝90°，M，N的高度差GH＝51cm，N，F的水平距离NH＝3cm，若该台灯底座高度AB＝4cm，则点O到桌面BC的距离为 cm．

查看试题解析

三、解答题（本题有6小题，共46分．）

19.

(1)、计算： $\sqrt{3} \times \sqrt{6} - \sqrt{8} + \sqrt{(- 2)^{2}}$ ；

(2)、解方程：x²-2x-3＝0．

查看试题解析
20. 如图，在6×6网格中，每个正方形的边长为1，请按照下面要求作图．

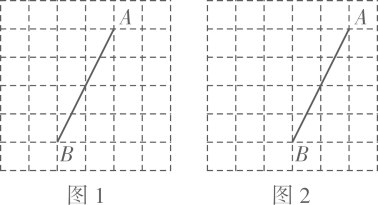(1)、在图1中画一个面积为8的▱ABCD，且C，D在格点上．

(2)、在图2中画一个三边均为无理数的Rt△ABE，且点E在格点上．

查看试题解析
21. 质量检测部门对甲、乙两公司销售的某电子产品的使用寿命进行跟踪调查，各抽查了10件产品，统计结果如表：
甲公司被抽查的电子产品使用寿命统计表

时间（年）

6

7

8

10

11

数量（个）

2

3

2

2

1

乙公司被抽查的电子产品使用寿命统计表

时间（年）

5

6

9

11

13

数量（个）

2

4

1

1

2

(1)、求甲、乙两公司被抽查的电子产品的平均使用寿命．

(2)、若你是顾客，从平均数、中位数、众数的这三个角度进行分析，你将选购哪家公司销售的产品？

查看试题解析
22. 如图，在▱ABCD中，对角线AC与BD相交于点O，点E，F分别为BO，OD的中点，连结AE，CF．

(1)、求证：AE＝CF．

(2)、若∠BAC＝90°，AB＝3，AE＝ $\frac{\sqrt{13}}{2}$ ，求▱ABCD的周长．

查看试题解析

23. 根据以下销售情况，解决销售任务．

	销售情况分析
	总公司将一批衬衫由甲、乙两家分店共同销售，因地段不同，它们的销售情况如下：
店面	甲店	乙店
日销售情况	每天可售出20件，每件盈利40元．	每天可售出32件，每件盈利30元．
市场调查	经调查发现，每件衬衫每降价1元，甲、乙两家店一天都可多售出2件．
情况设置	设甲店每件衬衫降价a元，乙店每件衬衫降价b元．
任务解决
任务1	甲店每天的销售量 ▲ （用含a的代数式表示）．乙店每天的销售量 ▲ （用含b的代数式表示）．
任务2	当a＝5，b＝4时，分别求出甲、乙店每天的盈利．
任务3	总公司规定两家分店下降的价格必须相同，请求出每件衬衫下降多少元时，两家分店一天的盈利和为2244元．

查看试题解析

24. 如图1，在Rt△ABC中，∠B＝90°，AB＝3cm，BC＝4cm，过点C作CG∥AB，CD平分∠ACG交射线BA于点D．

(1)、求CD的长．

(2)、如图2，点P从点D出发向点B运动，速度为1cm/s，同时，点M从点C出发，沿着射线CG方向运动，速度为2cm/s，连结PM．设运动时间为t（s）（0＜t＜8）．
①当PM与△ACD的一条边相等时，求t的值．
②当A关于PM的对称点A'落在CG上时，求t的值．

查看试题解析

每天使用零花钱（单位：元）	10	15	20	25	30
人数	1	3	6	5	5

时间（年）	6	7	8	10	11
数量（个）	2	3	2	2	1

时间（年）	5	6	9	11	13
数量（个）	2	4	1	1	2