浙江省宁波市慈溪市2022-2023学年七年级下学期期中数学试卷

试卷更新日期：2023-05-24 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，共30.0分。）

1. 下列图形中， $∠ 1$ 与 $∠ 2$ 不是同位角的是（）

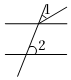A、 B、 C、 D、

查看试题解析
2. 某细胞的直径约为0.000123毫米，将0.000123用科学记数法表示为（）

A、 $0.123 \times 1 0^{- 3}$ B、 $1.23 \times 1 0^{- 3}$ C、 $123 \times 1 0^{- 4}$ D、 $1.23 \times 1 0^{- 4}$

查看试题解析
3. 下列分式中，最简分式是（）

A、 $\frac{a + 1}{a^{2} - 1}$ B、 $\frac{4 a}{6 {bc}^{2}}$ C、 $\frac{2 a}{2 - a}$ D、 $\frac{a + b}{a^{2} + ab}$

查看试题解析
4. 下列因式分解正确的是（）

A、 $a^{3} + a^{2} + a = a (a^{2} + a)$ B、 $4 x^{2} - 4 x + 1 = {(2 x - 1)}^{2}$ C、 $- 2 a^{2} + 4 a = - 2 a (a + 2)$ D、 $x^{2} - 3 x + 1 = x (x - 3) + 1$

查看试题解析
5. 下列运算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 ${(a + 3)}^{2} = a^{2} + 9$ C、 ${(2 x y^{2})}^{3} = 2 x^{3} y^{6}$ D、 $a^{5} \div a^{2} = a^{3}$

查看试题解析
6. 若关于 $x$ ， $y$ 的二元一次方程组 ${\begin{array}{l} x + 2 y = 2 ① \\ 2 x + y = a ② \end{array}$ 的解满足 $x + y = 5$ ，则 $a$ 的值为（）

A、13 B、14 C、15 D、16

查看试题解析
7. 将分式 $\frac{x + y}{x^{2} + y^{2}}$ 中 $x$ 与 $y$ 的值同时扩大为原来的3倍，分式的值（）

A、扩大3倍 B、缩小3倍 C、不变 D、无法确定

查看试题解析
8. 如图，将一条两边沿互相平行的纸带折叠．若 $∠ 1 ： ∠ 2 = 4 ： 3$ ，则 $∠ 3$ 的度数是（）

A、100° B、105° C、108° D、144°

查看试题解析
9. 如图，利用两块相同的长方体木块（阴影部分）测量一件长方体物品的高度，首先按左图方式放置，再按右图方式放置，测量的数据如图，则长方体物品的高度是（）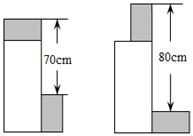

A、73cm B、74cm C、75cm D、76cm

查看试题解析
10. 已知m，n均为正整数且满足 $m n - 2 m - 3 n - 20 = 0$ ，则 $m + n$ 的最小值是（　　）

A、20 B、30 C、32 D、37

查看试题解析

二、填空题（本大题共6小题，共24.0分）

11. 因式分解： $a^{3} - 9 a =$ .

查看试题解析
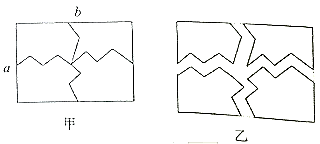
12. 若分式 $\frac{x - 1}{x + 3}$ 的值为0，则x= ．

查看试题解析
13. 若关于x、y的二元一次方程组 ${\begin{matrix} x + y = 5 k \\ x - y = 9 k \end{matrix}$ 的解也是二元一次方程 $2 x + 3 y = 6$ 的解，则k的值为.

查看试题解析
14. 一块长为a（cm），宽为 $b$ （cm）的长方形地板，中间有两条裂缝（如图甲）.若移动后，两条裂缝都相距1cm（如图乙），则产生的裂缝的面积是平方厘米.

查看试题解析
15. 关于 $x$ 的分式方程 $\frac{k - 1}{x^{2} - 1} - \frac{1}{x - 1} = \frac{k}{x + 1}$ 有增根，则 $k =$ .

查看试题解析
16. 如图，图 $1$ 是一盏可折叠台灯，图2为其平面示意图，底座 $A O ⊥ O E$ 于点 $O$ ，支架 $A B$ ， $B C$ 为固定支撑杆， $∠ B A O$ 是 $∠ C B A$ 的两倍，灯体 $C D$ 可绕点 $C$ 旋转调节，现把灯体 $C D$ 从水平位置旋转到位置 $($ 如图 $2$ 中虚线所示 $)$ ，此时，灯体 $C D'$ 所在的直线恰好垂直支架 $A B$ ，且 $∠ B C D - ∠ D C D' = 114 °$ ，则 $∠ D C D' =$ ．

查看试题解析

三、解答题（本大题共8小题，共66.0分。）

17. 计算：

(1)、 $(- 1)^{2012} + (- \frac{1}{2})^{- 2} - (3.14 - π)^{0}$ ；

(2)、 $(x + 1) (x - 3) - (x + 1)^{2}$ ．

查看试题解析
18. 解方程（组）：

(1)、 ${\begin{array}{l} x - 3 y = 4 \\ 2 x - y = 3 \end{array}$ ．

(2)、 $\frac{1}{x - 2} + 3 = \frac{1 - x}{2 - x}$ ．

查看试题解析
19. 先化简，再求值： $(\frac{2 x - 3}{x - 2} - 1) \div \frac{x^{2} - 2 x + 1}{x - 2}$ ，然后再从1，2，3中选一个你喜欢的数，求式子的值．

查看试题解析
20. 如图，已知 $∠ 1 + ∠ 2 = 180 °$ ， $∠ B = ∠ E$ ．

(1)、试猜想 $A B$ 与 $C E$ 之间有怎样的位置关系？并说明理由．

(2)、若 $C A$ 平分 $∠ B C E$ ， $∠ B = 50 °$ ，求 $∠ A$ 的度数．

查看试题解析
21. 临近春节，水果持续畅销 $.$ 某水果商购进第一批30箱粑粑柑和20箱冰糖心苹果，共花费2700元，全部销售完 $.$ 同种水果进价不变，水果商又购进第二批50箱粑粑柑和40箱冰糖心苹果，共花费4800元．

(1)、请你计算粑粑柑 $.$ 冰糖心苹果每箱进价各多少元？

(2)、水果商以粑粑柑80元 $/$ 箱、冰糖心苹果60元 $/$ 箱销售，50箱粑粑柑和20箱冰糖心苹果很快销售完 $.$ 接下来，水果商下调冰糖心苹果价格的10%，销售完10箱后，再次下调冰糖心苹果价格的10%销售完剩下的箱，水果商销售第二批水果获得的利润是多少？

查看试题解析
22. 图1是一个长为 $2 a$ 、宽为 $2 b$ 的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．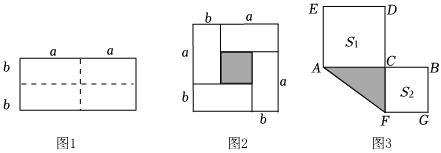

(1)、观察图2，请你写出下列三个代数式 $(a + b)^{2}$ ， $(a - b)^{2}$ ， $a b$ 之间的等量关系为．

(2)、运用你所得到的公式，计算：若 $m$ 、 $n$ 为实数，且 $m n = - 3$ ， $m - n = 4$ ，试求 $m + n$ 的值．

(3)、如图3，点 $C$ 是线段 $A B$ 上的一点，以 $A C$ 、 $B C$ 为边向两边作正方形，设 $A B = 8$ ，两正方形的面积和 $S_{1} + S_{2} = 32$ ，求图中阴影部分面积．

查看试题解析
23. 数学教科书中这样写道：
“我们把多项式 $a^{2} + 2 a b + b^{2}$ 及 $a^{2} - 2 a b + b^{2}$ 叫做完全平方式”，如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法，配方法是一种重要的解决问题的数学方法，经常用来解决一些与非负数有关的问题或求代数式最大值，最小值等．

例如： $x^{2} + 2 x - 3 = (x^{2} + 2 x + 1) - 4 = (x + 1)^{2} - 4$ ；

例如求代数式 $2 x^{2} + 4 x - 6$ 的最小值； $2 x^{2} + 4 x - 6 = 2 (x^{2} + 2 x - 3) = 2 (x + 1)^{2} - 8$ ．

根据阅读材料用配方法解决下列问题：

(1)、分解因式： $m^{2} - 6 m + 5$ ；

(2)、当 $a$ ， $b$ 为何值时，多项式 $a^{2} + b^{2} - 4 a + 10 b + 33$ 有最小值，并求出这个最小值；

(3)、已知 $a - b = 8$ ， $a b + c^{2} - 4 c + 20 = 0$ ，求 $a + b + c$ 的值．

查看试题解析
24. 阅读：在分式中，当分子的次数大于或等于分母的次数时，我们称之为“假分式”，例如： $\frac{x - 1}{x + 1} ， \frac{x^{2}}{x + 2}$ 这样的分式就是假分式；当分子的次数小于分母的次数时，我们称之为“真分式”，例如： $\frac{1}{x + 1}$ ， $- \frac{2 x}{x^{2} - 1}$ 这样的分式就是真分式，我们知道，假分数可以化为带分数，例如： $\frac{8}{3} = \frac{3 \times 2 + 2}{3} = 3 \frac{2}{3}$ ，类似地，假分式也可以化为“带分式”，即整式与真分式的和的形式，
例如： $\frac{x^{2} + 2 x - 1}{x + 2} = \frac{x (x + 2) - 1}{x + 2} = x - \frac{1}{x + 2} ； \frac{x^{2}}{x + 2} = \frac{(x^{2} + 2 x) - 2 x}{x + 2} = \frac{x (x + 2) - 2 x - 4}{x + 2} = \frac{x (x + 2)}{x + 2} \frac{- 2 (x + 2) + 4}{x + 2} = x - 2 + \frac{4}{x + 2}$ ．

请根据上述材料，解答下列问题：

(1)、填空： $①$ 分式 $\frac{2}{x + 2}$ 是分式 $($ 填“真”或“假” $)$ ；
$②$ 把下列假分式化成一个整式与一个真分式的和 $($ 差 $)$ 的形式：
$\frac{x^{2} + 2 x - 13}{x - 3} =$ $+$ ．

(2)、把分式 $\frac{x^{2} + 2 x - 13}{x - 3}$ 化成一个整式与一个真分式的和 $($ 差 $)$ 的形式，并求 $x$ 取何整数时，这个分式的值为整数．

(3)、一个三位数 $m$ ，个位数字是百位数字的两倍，另一个两位数 $n$ ，十位数字与 $m$ 的百位数字相同，个位数字与 $m$ 的十位数字相同 $.$ 若这个三位数的平方能被这个两位数整除，求满足条件的两位数 $n$ ．

查看试题解析