浙江省宁波市北仑区精准联盟2022-2023学年八年级下学期期中数学试卷
试卷更新日期:2023-05-24 类型:期中考试
一、选择题(本大题共10小题,共40.0分。)
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 观察下列图形,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列二次根式是最简二次根式的是( )
3. 下列二次根式是最简二次根式的是( )
A、 B、 C、 D、4. 将通过配方转变为的形式,下列结果正确的是( )A、 B、 C、 D、5. 如图,在四边形ABCD中,对角线AC和BD相交于点O , 下列条件不能判断四边形ABCD是平行四边形的是( )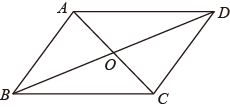 A、 , B、 , C、 , D、 ,6. 若样本 , , , 的平均数为 , 方差为 , 则对于样本 , , , , 下列结论正确的是( )A、平均数为 , 方差为 B、平均数为 , 方差为 C、平均数为 , 方差为 D、平均数为 , 方差为7. 用反证法证明“若 , , 则”时,应假设
A、 , B、 , C、 , D、 ,6. 若样本 , , , 的平均数为 , 方差为 , 则对于样本 , , , , 下列结论正确的是( )A、平均数为 , 方差为 B、平均数为 , 方差为 C、平均数为 , 方差为 D、平均数为 , 方差为7. 用反证法证明“若 , , 则”时,应假设 ( ) A、不垂直于 B、 , 都不垂直于 C、与相交 D、8. 如图,某校团委准备在艺术节期间举办学生绘画展览,为美化画面,在长为、宽为的矩形画面四周镶上宽度相等的彩纸,并使彩纸的面积恰好与原画面面积相等,若设彩纸的宽度为 , 根据题意可列方程( )
( ) A、不垂直于 B、 , 都不垂直于 C、与相交 D、8. 如图,某校团委准备在艺术节期间举办学生绘画展览,为美化画面,在长为、宽为的矩形画面四周镶上宽度相等的彩纸,并使彩纸的面积恰好与原画面面积相等,若设彩纸的宽度为 , 根据题意可列方程( ) A、 B、 C、 D、9. 若关于的一元二次方程有一根为 , 则关于的一元二次方程必有一根为( )A、 B、 C、2023 D、-202310. 如图所示,点为▱内一点,连接 , , , , , 已知的面积为 , 的面积为 , 则阴影部分的面积为( )
A、 B、 C、 D、9. 若关于的一元二次方程有一根为 , 则关于的一元二次方程必有一根为( )A、 B、 C、2023 D、-202310. 如图所示,点为▱内一点,连接 , , , , , 已知的面积为 , 的面积为 , 则阴影部分的面积为( ) A、6 B、8 C、10 D、12
A、6 B、8 C、10 D、12二、填空题(本大题共6小题,共30.0分)
-
11. 若式子有意义,则x的取值范围是 .12. 如果一个边形的内角和等于它的外角和的4倍,则 .13. 某校规定学生的体育成绩由三部分组成,早晨锻炼及体育课外活动表现占成绩的25%,体育理论测证占25%,体育技能测试占50%,小明的上述三项成绩依次是94分,90分,96分,则小明这学期的体育成绩是 分14. 对于实数 , , 定义运算“”如下: , 例如, , 若 , 则的值为 .15. 如图,为的中位线,点在上,且 , 若 , , 则的长为 .
 16. 如图,在平行四边形中, , 是的中点,作 , 垂足在线段上,连接 , , 则以下结论:;;;其中正确的结论序号为 .
16. 如图,在平行四边形中, , 是的中点,作 , 垂足在线段上,连接 , , 则以下结论:;;;其中正确的结论序号为 .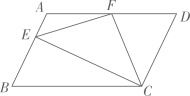
三、解答题(本大题共8小题,共80.0分。)
-
17. 计算:(1)、;(2)、 .18. 解下列方程:(1)、;(2)、 .19. 如图,在的网格中,每个小正方形的边长都是1,点 , , 均在格点上.
 (1)、在图1中,作一个各顶点均在格点上的▱ , 使得为对角线交点;(2)、在图2中,作一个各顶点均在格点上的▱ , 使其面积等于8,且该平行四边形的一条边等于其一条对角线.20. 我市某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
(1)、在图1中,作一个各顶点均在格点上的▱ , 使得为对角线交点;(2)、在图2中,作一个各顶点均在格点上的▱ , 使其面积等于8,且该平行四边形的一条边等于其一条对角线.20. 我市某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
平均分(分)
中位数(分)
众数(分)
方差(分2)
初中部
85
高中部
85
100
160
(1)、根据图示计算出、、的值;(2)、计算初中代表队决赛成绩的方差 , 并判断哪一个代表队选手成绩较为稳定.21. 某超市于今年年初以每件25元的进价购进一批商品当商品售价为40元时,一月份销售256件二、三月该商品十分畅销销售量持续走高在售价不变的基础上,三月底的销售量达到400件设二、三这两个月的月平均增长率不变.(1)、求二、三这两个月的月平均增长率;(2)、从四月份起,商场决定采用降价促销的方式回馈顾客,经调查发现,该商品每降价1元,销售量增加5件,当商品降价多少元时,商场获利4250元?22. 如图,已知在▱中,对角线 , 交于点 , , , 分别在线段 , 上,且 , 连接 , . (1)、求证:;(2)、若 , .
(1)、求证:;(2)、若 , .求的长;
求直线与之间的距离.
23. 已知关于的一元二次方程 , 其中 , , 分别为三边的长.(1)、如果是方程的根,试判断的形状,并说明理由;(2)、如果方程有两个相等的实数根,试判断的形状,并说明理由;(3)、如果是等边三角形,试求这个一元二次方程的根.24. 在直角坐标系中,如图1, , 点的坐标为 , , 点坐标为 , 点是射线上的动点,满足 , 以 , 为邻边作▱ . (1)、当时,求出的长度;(2)、当时,是否存在的值,使得▱的面积等于面积的 , 若存在,求出的值;若不存在,请说明理由;(3)、当点在第四象限时,点关于点的对称点为 , 点刚好落在直线上时,求的值直接写出答案 .
(1)、当时,求出的长度;(2)、当时,是否存在的值,使得▱的面积等于面积的 , 若存在,求出的值;若不存在,请说明理由;(3)、当点在第四象限时,点关于点的对称点为 , 点刚好落在直线上时,求的值直接写出答案 .