浙江省杭州市萧山区八校2022-2023学年七年级下学期期中数学试卷

试卷更新日期：2023-05-24 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，共30.0分。）

1. 下列方程是二元一次方程的是（）

A、 $\frac{x}{2} - y = 3 x$ B、 $2 x^{2} - 3 y = 5$ C、 $x y = 3 x + 7$ D、 $\frac{2}{x} - 3 y = \frac{1}{2}$

查看试题解析
2. 下列运算中，正确的是（）

A、 $(a^{2})^{3} = a^{8}$ B、 $(- 3 a)^{2} = 6 a^{2}$ C、 $a^{2} \cdot a^{3} = a^{5}$ D、 $a b^{2} + 2 a b^{2} = 2 a^{2} b^{4}$

查看试题解析
3. 北斗卫星导航系统是中国自行研制的全球卫星导航系统，授时精度优于0.00000001秒，0.00000001用科学记数法可表示为（）

A、 $0.1 \times 1 0^{- 7}$ B、 $1 \times 1 0^{- 8}$ C、 $1 \times 1 0^{- 7}$ D、 $0.1 \times 1 0^{- 8}$

查看试题解析
4. 如图，下列条件能使 $A B / / C D$ 的是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ 3 = ∠ 4$ C、 $∠ 1 = ∠ 3$ D、 $∠ 2 = ∠ 4$

查看试题解析
5. 金山银山不如绿水青山，某地准备购买一些松树和梭梭树苗 $.$ 已知购买4棵松树苗和3棵梭梭树苗需要180元，购买1棵梭梭树苗比1棵松树苗少花费10元 $.$ 设每棵松树苗 $x$ 元，每棵梭梭树苗 $y$ 元，则列出的方程组正确的是（）

A、 ${\begin{array}{l} 4 x + 3 y = 180 \\ y - x = 10 \end{array}$ B、 ${\begin{array}{l} 3 x + 4 y = 180 \\ y - x = 10 \end{array}$ C、 ${\begin{array}{l} 3 x + 4 y = 180 \\ x - y = 10 \end{array}$ D、 ${\begin{array}{l} 4 x + 3 y = 180 \\ x - y = 10 \end{array}$

查看试题解析
6. 下列等式从左到右的变形是因式分解的是（）

A、 $8 a^{3} b^{2} = 2 a b \cdot 4 a^{2} b$ B、 $(y + 4) (y - 4) = y^{2} - 16$ C、 $x^{2} - 2 x + 1 = {(x - 1)}^{2}$ D、 $y^{2} - 2 x y + y = y (y - 2 x)$

查看试题解析
7. 如图， $l_{1} / / l_{2}$ ，则（）

A、 $α + β - γ = 180 °$ B、 $α + β = γ$ C、 $α + β + γ = 180 °$ D、 $α + β = 2 γ$

查看试题解析
8. 已知实数 $x$ ， $y$ ， $z$ 满足 ${\begin{array}{l} x + y + z = 7 \\ 4 x + y - 2 z = 2 \end{array}$ ，则代数式 $3 (x - z) + 1$ 的值是（）

A、-2 B、-4 C、-5 D、-6

查看试题解析
9. 式子 $(2 + 1) (2^{2} + 1) (2^{4} + 1) (2^{8} + 1) \dots (2^{1024} + 1) + 1$ 化简的结果为（）

A、 $2^{1010} + 1$ B、 $2^{1010}$ C、 $2^{2020} + 1$ D、 $2^{2048}$

查看试题解析
10. 如图，已知 $A B / / C D$ ， $∠ M B N = \frac{3}{2} ∠ A B M$ ， $∠ M D N = \frac{3}{2} ∠ C D M .$ 则 $∠ M$ 与 $∠ N$ 之间满足的数量关系是（）

A、 $∠ M = ∠ N$ B、 $2 ∠ N + 5 ∠ M = 720 °$ C、 $∠ M + ∠ M = 720 °$ D、 $5 ∠ N + 6 ∠ M = 360 °$

查看试题解析

二、填空题（本大题共6小题，共24.0分）

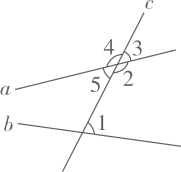
11. 已知二元一次方程 $2 x - 3 y = 5$ 有一组解为 ${\begin{array}{l} x = m \\ y = 1 \end{array}$ ，则 $m =$ ．

查看试题解析
12. 已知直线a、b被直线c所截，则与∠1是内错角关系的是.

查看试题解析
13. 如果 $a + b = 5$ ， $a b = 7$ ，则 $a^{2} b + a b^{2}$ 的值为．

查看试题解析
14. 如图，一块含 $30 °$ 角的三角板在直线 $a$ 、 $b$ 之间，已知直线 $a / / b$ ，直线 $c$ 分别与直线 $a$ ， $b$ 相交， $∠ 1 = 60 °$ ，则 $∠ 2$ 的度数为 $° .$

查看试题解析
15. 如图，将Rt△ABC沿着点B到C的方向平移到△DEF的位置，AB=9，DO=4，平移距离为6，则阴影部分面积为.

查看试题解析
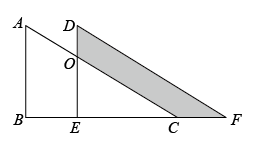16. 有两个正方形 $A$ ， $B$ ，将 $A$ ， $B$ 并列放置后构造新的长方形得到图甲，将 $A$ ， $B$ 并列放置后构造新的正方形得到图乙，若图甲和图乙中阴影部分的面积分别为10和32，则正方形 $B$ 的面积为．

查看试题解析

三、解答题（本大题共7小题，共66.0分。）

17. 解下列方程组：

(1)、 ${\begin{array}{l} y + 5 = x \\ 3 x + y = 3 \end{array}$ ；

(2)、 ${\begin{array}{l} 4 x - 4 y = 1 \\ 3 x + 2 y = 2 \end{array}$ ．

查看试题解析
18.

(1)、计算： $| - 3 | + (- 1)^{2023} \times (π - 3.14)^{0} - (- \frac{1}{2})^{- 2}$ ；

(2)、化简： $(- 2 x)^{2} \cdot (5 x^{2} y) \div x$ ；

(3)、分解因式： $3 x^{2} - 9 x y$ ．

查看试题解析
19. 化简，求值： $[(x - 2 y)^{2} + (x - 2 y) (x + 2 y) - 2 x (2 x - y)] \div (2 x)$ ，其中 $| x - 3 | + {(y + \frac{1}{2})}^{2} = 0$ ．

查看试题解析
20. 某中学组织一批学生春游，原计划租用45座客车若干辆，但有15人没有座位；若租用同样数量的60座客车，则多出一辆车，且其余客车恰好坐满.已知45座客车租金为每辆300元，60座客车租金为每辆400元，问：

(1)、这批学生的人数是多少？原计划租用多少辆45座客车？

(2)、若租用同一种车，要使每位学生都有座位，应该怎样租用才合算？

查看试题解析
21. 如图，已知 $∠ 1 = ∠ 2$ ， $∠ A = ∠ D$ .

(1)、判断 $A B$ 与 $C D$ 的位置关系，并说明理由

(2)、若 $∠ B F D = 40 °$ ，求 $∠ M E C$ 的度数

查看试题解析
22. 如图 $1$ 是一个长为 $4 a$ ，宽为b的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成一个如图 $2$ 的图形．

(1)、观察图形，请你写出 $(a + b)^{2}$ 、 $(a - b)^{2}$ 、 $a b$ 之间的等量关系式；

(2)、若 $x + \frac{1}{x} = 3$ ，利用（1）中的结论，求 $x - \frac{1}{x}$ 的值；

(3)、若 $(2021 - m) (2022 - m) = 4$ ，求 $(m - 2021)^{2} + (2022 - m)^{2}$ 的值．

查看试题解析
23. 如图，已知 $A M / / B N$ ，点 $P$ 是射线 $A M$ 上一动点 $($ 与点 $A$ 不重合 $)$ ， $B C$ ， $B D$ 分别平分 $∠ A B P$ 和 $∠ P B N$ ，分别交射线 $A M$ 于点 $C$ ， $D$ ．

(1)、当 $∠ A = 52 °$ 时， $∠ A B N$ 的度数是， $∠ C B D$ 的度数是；

(2)、当 $∠ A = x °$ 时，求 $∠ C B D$ 的度数 $($ 用含 $x$ 的式子表示 $)$ ；

(3)、当点 $P$ 运动到使 $∠ A C B = ∠ A B D$ ， $∠ A = x °$ 时，求 $∠ A B P$ 的度数 $($ 用含 $x$ 的代子表示 $)$ ．

查看试题解析