浙江省杭州市萧山区八校2022-2023学年八年级下学期期中数学试卷
试卷更新日期:2023-05-24 类型:期中考试
一、选择题(本大题共10小题,共30.0分。)
-
1. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、2. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、
 斐波那契螺旋线
B、
斐波那契螺旋线
B、 笛卡尔心形线
C、
笛卡尔心形线
C、 赵爽弦图
D、
赵爽弦图
D、 科克曲线
3. 若 , 则一元二次方程必有一根是( )A、0 B、1 C、-1 D、无法确定4. 有11位同学参加学校举行的歌唱比赛,比赛后根据每个学生的最后得分计算出中位数、平均数、众数和方差,如果去掉一个最高分和一个最低分,则一定不会发生变化的是( )A、中位数 B、平均数 C、众数 D、方差5. 如图,在▱中,若 , 则的度数是( )
科克曲线
3. 若 , 则一元二次方程必有一根是( )A、0 B、1 C、-1 D、无法确定4. 有11位同学参加学校举行的歌唱比赛,比赛后根据每个学生的最后得分计算出中位数、平均数、众数和方差,如果去掉一个最高分和一个最低分,则一定不会发生变化的是( )A、中位数 B、平均数 C、众数 D、方差5. 如图,在▱中,若 , 则的度数是( ) A、 B、 C、 D、6. 如果一组数据2,3,4,5, 的方差与另一组数据101,102,103,104,105的方差相等,那么 的值( )A、6 B、1 C、6或1 D、无法确定7. 如图,面积为的长方形试验田一面靠墙墙的长度不限 , 另外三面用长的篱笆围成,平行于墙的一边开有一扇宽的门门的材料另计设试验田垂直于墙的一边的长为 , 则所列方程正确的是( )
A、 B、 C、 D、6. 如果一组数据2,3,4,5, 的方差与另一组数据101,102,103,104,105的方差相等,那么 的值( )A、6 B、1 C、6或1 D、无法确定7. 如图,面积为的长方形试验田一面靠墙墙的长度不限 , 另外三面用长的篱笆围成,平行于墙的一边开有一扇宽的门门的材料另计设试验田垂直于墙的一边的长为 , 则所列方程正确的是( ) A、 B、 C、 D、8. 如图,在平行四边形 中, , 是对角线 上不同的两点,连接 , , , .下列条件中,不能得出四边形 一定是平行四边形的为( )
A、 B、 C、 D、8. 如图,在平行四边形 中, , 是对角线 上不同的两点,连接 , , , .下列条件中,不能得出四边形 一定是平行四边形的为( )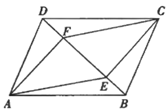 A、 B、 C、 D、9. 已知关于的方程, , 则下列说法正确的是( )A、不存在的值,使得方程有两个相等的实数解 B、至少存在一个的值,使得方程没有实数解 C、无论为何值,方程总有一个固定不变的实数根 D、无论为何值,方程有两个不相等的实数根10. 如图,在 ABCD中,∠ABC=45°,BC=4,点F是CD上一个动点,以FA、FB为邻边作另一个 AEBF,当F点由D点向C点运动时,下列说法正确的选项是( )
A、 B、 C、 D、9. 已知关于的方程, , 则下列说法正确的是( )A、不存在的值,使得方程有两个相等的实数解 B、至少存在一个的值,使得方程没有实数解 C、无论为何值,方程总有一个固定不变的实数根 D、无论为何值,方程有两个不相等的实数根10. 如图,在 ABCD中,∠ABC=45°,BC=4,点F是CD上一个动点,以FA、FB为邻边作另一个 AEBF,当F点由D点向C点运动时,下列说法正确的选项是( )① AEBF的面积先由小变大,再由大变小;② AEBF的面积始终不变;③线段EF最小值为
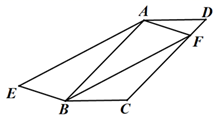 A、① B、② C、①③ D、②③
A、① B、② C、①③ D、②③二、填空题(本大题共6小题,共24.0分)
-
11. 若二次根式 有意义,则x的取值范围是 .12. 正边形的一个内角为 , 则 .13. 已知一组数据 , , , 的平均数是 , 则数据 , , , 的平均数是 .14. 已知 , , 则.15. 已知实数 , 满足 , 则代数式的最小值是 .16. 如图,在▱中, , , ▱的面积为 , 动点从点出发,以1个单位长度的速度沿线段向终点运动,同时动点从点出发以3个单位长度的速度在间往返运动,当点到达点时,动点、同时停止运动,连结设运动时间为秒.
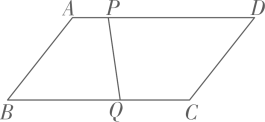 (1)、则和之间的距离为 ;(2)、当平分▱的面积时,则 .
(1)、则和之间的距离为 ;(2)、当平分▱的面积时,则 .三、解答题(本大题共7小题,共66.0分。)
-
17. 计算下列各式:(1)、(2)、18. 解下列方程:(1)、;(2)、 .19. 2023年大年初一上映两部电影,满江红和流浪地球 , 为了解学生对这两部影片的评价,某调查小组从该校八年级中随机抽取了20名学生对这两部作品分别进行打分满分10分 , 并进行整理、描述和分析,下面给出了部分信息.
《满江红》得分情况:7,8,7,10,7,6,9.9,10,10,8.9,8,6,6,10,
9,7,9,9.
抽取的学生对两部作品分别打分的平均数,众数和中位数:
平均数
众数
中位数
满江红
8.2
9
流浪地球
7.8
8

根据图表信息,解答下列问题:
(1)、直接写出图表中的 , , 的值;(2)、根据上述数据,你认为该校八年级学生对哪部作品评价更高?请说明理由.20. 如图,在▱中,平分交于点 , 交于点 , 平分交于点 .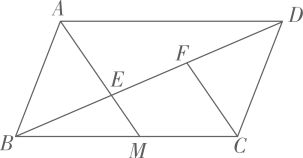 (1)、求证:;(2)、若 , 求的度数.21. 今年大德福超市以每件25元的进价购进一批商品,当商品售价为40元时,三月份销售256件,四、五月该商品十分畅销,销售量持续上涨,在售价不变的基础上,五月份的销售量达到400件.(1)、求四、五这两个月的月平均增长率.(2)、从六月份起,商场为了减少库存,从而采用降价促销方式,经调查发现,该商品每降价1元,月销量增加5件,当商品降价多少元时,商场月获利4250元?
(1)、求证:;(2)、若 , 求的度数.21. 今年大德福超市以每件25元的进价购进一批商品,当商品售价为40元时,三月份销售256件,四、五月该商品十分畅销,销售量持续上涨,在售价不变的基础上,五月份的销售量达到400件.(1)、求四、五这两个月的月平均增长率.(2)、从六月份起,商场为了减少库存,从而采用降价促销方式,经调查发现,该商品每降价1元,月销量增加5件,当商品降价多少元时,商场月获利4250元?
