浙江省杭州市萧山区2022-2023学年九年级下学期期中数学试卷
试卷更新日期:2023-05-24 类型:期中考试
一、选择题(本大题共10小题,共30.0分。)
-
1. 下列等式正确的是( )A、 B、 C、 D、2. 如图, , , 相交于点若 , , :( )
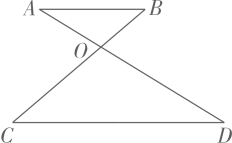 A、1:2 B、1:4 C、2:1 D、4:13. 两枚同样的硬币同时抛出,落地后一个正面朝上、一个反面朝上的概率是( )A、1 B、 C、 D、4. 如图,边长相等的正五边形和正六边形如图拼接在一起,则的度数为( )
A、1:2 B、1:4 C、2:1 D、4:13. 两枚同样的硬币同时抛出,落地后一个正面朝上、一个反面朝上的概率是( )A、1 B、 C、 D、4. 如图,边长相等的正五边形和正六边形如图拼接在一起,则的度数为( )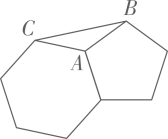 A、 B、 C、 D、5. 在中, , , , 则的长为( )A、 B、 C、 D、6. 如图,在中,是直径,是弦若 , 则( )
A、 B、 C、 D、5. 在中, , , , 则的长为( )A、 B、 C、 D、6. 如图,在中,是直径,是弦若 , 则( )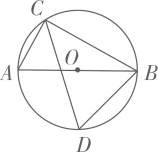 A、 B、 C、 D、7. 如图,已知 , 点是边中点,且若 , 则( )
A、 B、 C、 D、7. 如图,已知 , 点是边中点,且若 , 则( )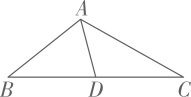 A、3 B、4 C、 D、8. 已知二次函数 , 与的部分对应值为:
A、3 B、4 C、 D、8. 已知二次函数 , 与的部分对应值为:-2
-1
0
1
2
-1
2
3
2
?
关于此函数的图象和性质,下列说法正确的是( )
A、当时,函数图象从左到右上升 B、抛物线开口向上 C、方程的一个根在-2与-1之间 D、当时,9. 如图, 经过 的顶点C,与边 分别交于点M,N,与 边相切.若 ,则线段 长度的最小值是( )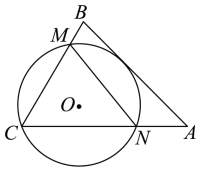 A、3 B、2 C、2 D、10. 如图,在中, , , 点在边上, , 分别为 , 的中点,连接过点作的垂线,与 , 分别交于 , 两点连接 , 交于点有以下判断:; , 且;当时,的面积为;的最大值为其中正确的是( )
A、3 B、2 C、2 D、10. 如图,在中, , , 点在边上, , 分别为 , 的中点,连接过点作的垂线,与 , 分别交于 , 两点连接 , 交于点有以下判断:; , 且;当时,的面积为;的最大值为其中正确的是( ) A、①③ B、①③④ C、①②④ D、①②③④
A、①③ B、①③④ C、①②④ D、①②③④二、填空题(本大题共6小题,共24.0分)
-
11. 某平台进行“天宫课堂”中国空间站全程直播.某一时刻观看人数达到3790000人.用科学记数法表示3790000= .12. 因式分解: .13. 若⊙O中,弦AB的长度是半径的倍,则弦AB所对圆周角的度数为°.14. 已知函数 , 点在函数图象上当时, .15. 如图,在等腰中, , , 在上,且 , 则 .
 16. 已知二次函数当时,的取值范围是 , 该二次函数的对称轴为 , 则的取值范围是 .
16. 已知二次函数当时,的取值范围是 , 该二次函数的对称轴为 , 则的取值范围是 .三、解答题(本大题共7小题,共66.0分。)
-
17. 如图,三个顶点的坐标分别为 , , .
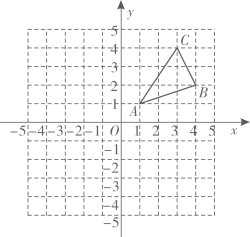 (1)、请在图中作出绕点逆时针方向旋转后得到的图形:(2)、求点运动到点所经过的路径的长结果保留 .18. 如图,在中,是角平分线,点是边上一点,且满足 .
(1)、请在图中作出绕点逆时针方向旋转后得到的图形:(2)、求点运动到点所经过的路径的长结果保留 .18. 如图,在中,是角平分线,点是边上一点,且满足 . (1)、证明: .(2)、若 , , 求的长.19. 一个不透明的布袋中有完全相同的四个小球,编号为1,2,3,4.甲和乙做游戏:从布袋中随机抽取一个小球,记下标号后,不放回;再从布袋中随机抽取一个小球,记下标号.若两次抽取的小球标号之和为奇数,甲赢;若标号之和为偶数,则乙赢.(1)、用画树状图或列表的方法,表示出两次取出编号的所有可能;(2)、判断这个游戏是否公平,并说明理由.20. 如图,以四边形的对角线为直径作圆,圆心为 , 过点作的延长线于点 , 已知平分 .
(1)、证明: .(2)、若 , , 求的长.19. 一个不透明的布袋中有完全相同的四个小球,编号为1,2,3,4.甲和乙做游戏:从布袋中随机抽取一个小球,记下标号后,不放回;再从布袋中随机抽取一个小球,记下标号.若两次抽取的小球标号之和为奇数,甲赢;若标号之和为偶数,则乙赢.(1)、用画树状图或列表的方法,表示出两次取出编号的所有可能;(2)、判断这个游戏是否公平,并说明理由.20. 如图,以四边形的对角线为直径作圆,圆心为 , 过点作的延长线于点 , 已知平分 . (1)、求证:是的切线;(2)、若 , , 求的半径和的长.21. 如图,在△ABC中,CD是边AB上的中线,∠B是锐角,sinB= ,tanA= ,AC= ,
(1)、求证:是的切线;(2)、若 , , 求的半径和的长.21. 如图,在△ABC中,CD是边AB上的中线,∠B是锐角,sinB= ,tanA= ,AC= ,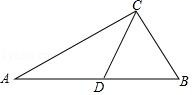 (1)、求∠B 的度数和 AB 的长.(2)、求 tan∠CDB 的值.
(1)、求∠B 的度数和 AB 的长.(2)、求 tan∠CDB 的值.
