浙江省杭州市西湖区2022-2023学年八年级下学期期中数学试卷

试卷更新日期：2023-05-24 类型：期中考试

进入出卷网下载

一、选择题（共10个小题，每题3分，共30分）

1. 下列图形是中心对称图形的是（　　）

A、有害垃圾 B、可回收物 C、厨余垃圾 D、其它垃圾

查看试题解析
2. 下列计算中，正确的是（）

A、 $\sqrt{{(- 3)}^{2}} = - 3$ B、 $\sqrt{8} + \sqrt{2} = \sqrt{10}$ C、 $3 \sqrt{2} - \sqrt{2} = 3$ D、 $\sqrt{8} \times \sqrt{2} = 4$

查看试题解析
3. 一个多边形的内角和为720°，那么这个多边形是（）

A、七边形 B、六边形 C、五边形 D、四边形

查看试题解析
4. 用配方法解方程x²-4x-6＝0时，原方程应变形为（）

A、（x+2）²＝10 B、（x+4）²＝22 C、（x-4）²＝22 D、（x-2）²＝10

查看试题解析
5. 已知m是方程x²-3x-1＝0的一个根，则代数式2m²-6m的值为（）

A、0 B、2 C、-2 D、4

查看试题解析
6. 某校八年级学生的平均年龄为14岁，年龄的方差为3，若学生人数没有变动，则两年后的同一批学生，对其年龄的说法正确的是（）

A、平均年龄为14岁，方差改变 B、平均年龄为16岁，方差不变 C、平均年龄为16岁，方差改变 D、平均年龄为14岁，方差不变

查看试题解析
7. 四边形ABCD的对角线AC、BD交于点O，下列条件不能判定四边形ABCD为平行四边形的是（）

A、 $∠ B A D = ∠ B C D$ ， $∠ A B C = ∠ A D C$ B、 $∠ A B C = ∠ A D C$ ， $A B ∥ C D$ C、 $A B ∥ C D$ ， $O B = O D$ D、 $A B = C D$ ， $O A = O C$

查看试题解析
8. 如图，在△ABC中，∠B＝90°，AB＝5cm，BC＝7cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC向点C以2cm/s的速度移动，当点Q到达点C时，P，Q均停止运动，若△PBQ的面积等于4cm² ，则运动时间为（）

A、1秒 B、4秒 C、1秒或4秒 D、1秒或 $\frac{27}{7}$ 秒

查看试题解析
9. 如图，▱ABCD与▱DCFE的周长相等，且∠BAD＝60°，∠F＝110°，则∠DAE的度数为（）

A、20° B、25° C、30° D、35°

查看试题解析
10. 如图在▱ABCD中，∠ABC＝60°，BC＝2AB＝8，点C关于AD的对称点为E，连接BE交AD于点F，点G为CD的中点，连接EG，BG．则△BEG的面积为（）

A、16 $\sqrt{3}$ B、14 $\sqrt{3}$ C、8 $\sqrt{3}$ D、7 $\sqrt{3}$

查看试题解析

二、填空题（共6个小题，每题4分，共24分）

11. $\sqrt{2^{2}}$ ＝

查看试题解析
12. 若二次根式 $\sqrt{2 - a}$ 有意义，则实数a的取值范围是.

查看试题解析
13. 一组数据3，2，x，1，5的众数是5，则这组数据的中位数是．

查看试题解析
14. 如图，已知平行四边形对角线AC、BD相交于点O，点E、F分别是线段AO、BO的中点．若AC+BD＝26cm，△OAB的周长是16cm，则EF＝cm．

查看试题解析
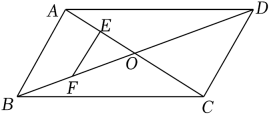15. 如图，△ABC中，AB＝3，AC＝5，若线段AO为BC边上的中线，则线段AO的取值范围为．

查看试题解析
16. 如图，在△ABC中，∠BAC＝90°，∠B＝45°，过点A作AD∥BC，且点D在点A的右侧，点P，Q分别是射线AD，射线CB上的一点，点E是线段CQ上的点，且CQ＝2AP，设AP＝x，CE为y，则y＝2x-2．当点Q为BC中点时，y＝3．

(1)、BC＝．

(2)、当AP＝时，使得以A，B，E，P为顶点的四边形是平行四边形．

查看试题解析

三、解答题（共7小题，共66分）

17. 解答下列各题．

(1)、 $\sqrt{24} + \sqrt{3} \times \sqrt{2}$ ；

(2)、 $(\sqrt{3} + 1) (\sqrt{3} - 1) + 1$ ．

查看试题解析
18. 用合适的方法解方程：

(1)、x²+2x＝0；

(2)、x²-5x+4＝0．

查看试题解析
19. 一次学情检测中，A，B，C，D，E五位同学的数学、英语成绩有如下信息：

A
B
C
D
E
平均分
方差
数学
71
68
72
69
70
70
2
英语
85
88
82
84
86
85
S²

(1)、求这五位同学在本次考试中英语成绩的方差S²；

(2)、学校进行“达人”社团招新，通过初期筛选，现以本次检测的数学、英语成绩为依据在A、B两位同学中取得分高的录取，规定数学成绩占60%，英语成绩占40%来计算总得分，请问哪位同学得分高，能够被“达人”社团录取？

查看试题解析
20. 如图所示，在▱ABCD中，点E，点F分别是AD，BC的中点，连接BE，DF．

(1)、求证：四边形BEDF是平行四边形．

(2)、若BC＝2 $\sqrt{2}$ ， ∠C＝105°，∠CBE＝45°，求线段DF的长度．

查看试题解析
21. 已知△ABC的两边AB，AC的长是关于x的一元二次方程x²-2（n-1）x+n²-2n＝0的两个根，第三边BC的长是10．

(1)、求证：无论n取何值，此方程总有两个不相等的实数根．

(2)、当n为何值时，△ABC为等腰三角形？并求△ABC的周长．

(3)、当n为何值时，△ABC是以BC为斜边的直角三角形？

查看试题解析
22. 社区利用一块矩形空地建了一个小型停车场，其布局如图所示．已知AD＝52m，AB＝28m，阴影部分设计为停车位，要铺花砖，其余部分均为宽度为x米的道路．已知铺花砖的面积为640m² ．

(1)、求道路的宽是多少米？

(2)、该停车场共有车位50个，据调查分析，当每个车位的月租金为200元时，可全部租出；若每个车位的月租金每上涨5元，就会少租出1个车位．
①当每个车位的月租金上涨多少元时，停车场的月租金收入为10000元？
②求此停车场的月租金收入最多为多少元？

查看试题解析
23. 如图，在▱ABCD中，AD＝2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF．

(1)、求证： $∠ D C F = \frac{1}{2} ∠ B C D$ ；

(2)、若 $\frac{B E}{A E} = a$ ，设△BEC的面积为S₁ ， △EFC 的面积为S₂ ，求 $\frac{S_{2}}{S_{1}}$ 的值．（用含a的代数式来表示）

查看试题解析

	A	B	C	D	E	平均分	方差
数学	71	68	72	69	70	70	2
英语	85	88	82	84	86	85	S²