浙江省杭州市观城教育集团2022-2023学年八年级下学期期中数学试卷
试卷更新日期:2023-05-24 类型:期中考试
一、选择题(本大题共10小题,共30.0分。)
-
1. 下列各图形都由若干个小正方形构成,其中是中心对称图形的是( )A、
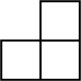 B、
B、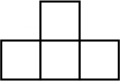 C、
C、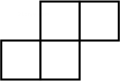 D、
D、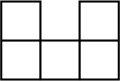 2. 以下各数是最简二次根式的是( )A、 B、 C、 D、3. 已知关于x的一元二次方程的一个根是 , 则m的值为( )A、2 B、4 C、-4 D、-24. 用反证法证明“若实数 , 满足 , 则 , 中至少有一个是”时,应先假设( )A、 , 中至多有一个是0 B、 , 中至少有两个是0 C、 , 中没有一个是0 D、 , 都等于05. 矩形具有而菱形不一定具有的性质是( )A、对角线互相垂直 B、对角线互相平分 C、对角线相等 D、对角线平分一组对角6. 如图,已知四边形 , 对角线和相交于 , 下面选项不能得出四边形
2. 以下各数是最简二次根式的是( )A、 B、 C、 D、3. 已知关于x的一元二次方程的一个根是 , 则m的值为( )A、2 B、4 C、-4 D、-24. 用反证法证明“若实数 , 满足 , 则 , 中至少有一个是”时,应先假设( )A、 , 中至多有一个是0 B、 , 中至少有两个是0 C、 , 中没有一个是0 D、 , 都等于05. 矩形具有而菱形不一定具有的性质是( )A、对角线互相垂直 B、对角线互相平分 C、对角线相等 D、对角线平分一组对角6. 如图,已知四边形 , 对角线和相交于 , 下面选项不能得出四边形是平行四边形的是( )
 A、 , 且 B、 , C、 , D、 , 且7. 若点 在反比例函数 为常数, 的图象上,则下列有关该函数的说法正确的是( )A、该函数的图象经过点 B、该函数的图象位于第一、三象限 C、 的值随 的增大而增大 D、当 时, 的值随 的增大而增大8. 对于一元二次方程 , 满足 , 且有两个相等的实数根,则( )A、 B、 C、 D、9. 如图,以和为两直角边作 , 再在斜边上截取 , 则的长是下列哪一个关于的方程的根( )
A、 , 且 B、 , C、 , D、 , 且7. 若点 在反比例函数 为常数, 的图象上,则下列有关该函数的说法正确的是( )A、该函数的图象经过点 B、该函数的图象位于第一、三象限 C、 的值随 的增大而增大 D、当 时, 的值随 的增大而增大8. 对于一元二次方程 , 满足 , 且有两个相等的实数根,则( )A、 B、 C、 D、9. 如图,以和为两直角边作 , 再在斜边上截取 , 则的长是下列哪一个关于的方程的根( )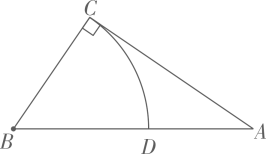 A、 B、 C、 D、10. 如图,正方形中,点 , , , 分别是各边的中点,连结 , 取的中点 , 连结 , , 则下列说法正确的是( )
A、 B、 C、 D、10. 如图,正方形中,点 , , , 分别是各边的中点,连结 , 取的中点 , 连结 , , 则下列说法正确的是( ) A、 B、四边形的周长是周长的倍 C、 D、四边形的面积是面积的倍
A、 B、四边形的周长是周长的倍 C、 D、四边形的面积是面积的倍二、填空题(本大题共6小题,共24.0分)
-
11. 要使式子有意义,则的取值范围是 .12. 一个多边形的内角和是720°,这个多边形的边数是 .13. 用一块长 , 宽的纸板,在四个角截去四个相同的小正方形,然后做成一个底面积为的无盖长方体纸盒,则截去的小正方形的边长为 .14. 若点 , 都在反比例函数的图象上,则 , , 的大小关系是 .15. 在三角形中,点 , , 分别是 , , 的中点,于点 , 若 , 则 .
 16. 如图,在矩形中,平分 , 交于点 , 交于点 , 以 , 为边,作矩形 , 与相交于点记四边形的面积为 , 四边形的面积为 , 若 , 则 .
16. 如图,在矩形中,平分 , 交于点 , 交于点 , 以 , 为边,作矩形 , 与相交于点记四边形的面积为 , 四边形的面积为 , 若 , 则 .
三、计算题(本大题共1小题,共10.0分)
-
17. 已知关于的方程有两个不相等的实数根.(1)、求的取值范围.(2)、是否存在实数 , 使此方程的两个实数根的倒数和等于1?若存在,求出的值:若不存在,说明理由.
四、解答题(本大题共6小题,共56.0分。)
-
18. 计算:(1)、;(2)、 .19. 解方程:(1)、;(2)、 .20. 如图,在四边形 中, , .
 (1)、求证:四边形 为平行四边形.(2)、若 , , ,求 的长.21. 如图,将一张矩形纸片沿直线折叠,使点落在点处,点落在点处,直线交于点 , 交于点 .
(1)、求证:四边形 为平行四边形.(2)、若 , , ,求 的长.21. 如图,将一张矩形纸片沿直线折叠,使点落在点处,点落在点处,直线交于点 , 交于点 . (1)、求证:四边形为菱形;(2)、若的面积与的面积比为4:1, , 求的长.22. 已知一次函数的图象与反比例函数的图象交于点 , .(1)、求 , 的值和反比例函数的表达式.(2)、设点 , 分别是两函数图象上的点在坐标系中画出和的图象,并根据图象直接写出,当时的取值范围;(3)、设 , 且 , 当时,;当时,圆圆说:“一定大于“你认为圆圆的说法正确吗?为什么?23. 如图1,已知正方形 , 是边上的一个动点不与点、重合 , 连结 , 点关于直线的对称点为 , 连结并延长交于点 , 连结 , .
(1)、求证:四边形为菱形;(2)、若的面积与的面积比为4:1, , 求的长.22. 已知一次函数的图象与反比例函数的图象交于点 , .(1)、求 , 的值和反比例函数的表达式.(2)、设点 , 分别是两函数图象上的点在坐标系中画出和的图象,并根据图象直接写出,当时的取值范围;(3)、设 , 且 , 当时,;当时,圆圆说:“一定大于“你认为圆圆的说法正确吗?为什么?23. 如图1,已知正方形 , 是边上的一个动点不与点、重合 , 连结 , 点关于直线的对称点为 , 连结并延长交于点 , 连结 , . (1)、求的度数.(2)、如图2,连结 , 若点为中点, , 求的面积.(3)、如图3,过点作于点 , 连结 , 请探究线段与的数量关系,并说明理由.
(1)、求的度数.(2)、如图2,连结 , 若点为中点, , 求的面积.(3)、如图3,过点作于点 , 连结 , 请探究线段与的数量关系,并说明理由.
-