广西北海市海城区2022-2023学年八年级下学期期中数学试卷
试卷更新日期：2023-05-24 类型：期中考试
一、选择题（共10小题，满分30分，每小题3分）
-
1. 下列图形中，是中心对称图形的是（ ）A、
B、
C、
D、
2. 下列二次根式中，最简二次根式是（ ）A、 B、 C、 D、3. 如果有意义，则a的取值范围是（ ）A、a≥0 B、a≤0 C、a≥3 D、a≤34. 在一个直角三角形中，有一个锐角等于60°，则另一个锐角的度数是（ ）A、120° B、90° C、60° D、30°5. 如图，在Rt△ABC中，CD是斜边AB上的中线，若∠A＝20°，则∠ACD＝（ ）
A、15° B、20° C、25° D、30°6. 将一元二次方程（x-2）（x+3）＝12化为一般形式ax2+bx+c＝0（a≠0，a，b，c为常数），其中c的值是（ ）A、-18 B、-6 C、6 D、187. 下列图各组数中，是勾股数的是（ ）A、6，8，12 B、0.6，0.8，1 C、8，15，16 D、9，12，158. 若将方程x2-6x-5＝0化成（x+a）2＝b（a，b为常数）的形式，则a+b的值是（ ）A、-17 B、-11 C、2 D、119. 我国古代数学著作《九章算术》记载了一道有趣的问题．原文是：今有池方一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐．问水深、葭长各几何．译为：有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺，如果把这根芦苇拉向水池一边，它的顶端恰好到达池边的水面，水的深度与这根芦苇的长度分别是多少？设芦苇的长度是x尺．根据题意，可列方程为（ ）
A、x2+102＝（x+1）2 B、（x-1）2+52＝x2 C、x2+52＝（x+1）2 D、（x-1）2+102＝x210. 如图，在Rt△ABC中，∠A＝90°，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，动点P从点B出发，沿着BC匀速向终点C运动，则线段EF的值大小变化情况是（ ）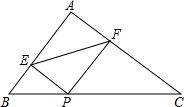
A、一直增大 B、不变 C、先减小后增大 D、先增大后减小二、填空题（共7小题，满分14分，每小题2分）
-
11. 分解因式：3m2-3＝ ．12. 七边形所有内角的度数之和是°.13. 化简所得的结果是.14. 已知一组数据2，2，8，x，7，4的中位数为5，则x的值是 ．15. 如图，直线a∥b∥c，AB⊥a，a与b的距离是2cm，b与c的距离是3cm，则a与c的距离是 cm．
16. 如图，在△ABC中，CD平分∠ACB交AB于点D，DE⊥AC交于点E，DF⊥BC于点F，且BC＝4，DE＝2，则△BCD的面积是 ．
17. 如图，矩形纸片ABCD中，AD＝10cm，AB＝4cm，按如图方式折叠，使点D与点B重合，折痕为EF，则AE＝cm．
三、解答题（共9小题，满分76分）
-
18. 计算：(1)、；(2)、19. 如图，矩形ABCD的对角线AC、BD相交于点O，CE∥BD，DE∥AC，若AC＝4，求四边形CODE的周长．
20. 如图，在Rt△ABC中，∠A＝90°，点D为斜边BC上一点，且BD＝BA，过点D作BC的垂线交AC于点E．求证：点E在∠ABC的角平分线上．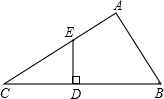
21. 已知关于x的一次函数y＝（3-m）x+m-5．(1)、若一次函数的图象过原点，求实数m的值；(2)、当一次函数的图象经过第二、三、四象限时，求实数m的取值范围．22. 如图，一次函数y＝x+3的图象l1与x轴相交于点B，与过点A（3，0）的一次函数的图象l2相交于点C（1，m）．
(1)、求一次函数图象l2相应的函数表达式；(2)、求△ABC的面积．23. 如图，在四边形ABCD中，AB∥DC，AB＝AD，对角线AC，BD交于点O，AC平分∠BAD，过点C作CE⊥AB交AB的延长线于点E，连接OE．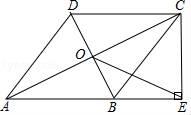
(1)、求证：四边形ABCD是菱形；(2)、若AB＝ ，BD＝2，求OE的长．24. 4月23日是世界读书日，习近平总书记说：“读书可以让人保持思想活力，让人得到智慧启发，让人滋养浩然正气”．某书店计划在“世界读书日”前夕，同时购进A，B两类图书，已知购进1本A类图书和2本B类图书共需135元；购进3本A类图书和4本B类图书共需305元．(1)、A，B两类图书每本的进价各是多少元？(2)、该书店计划购进A，B两类图书共90本，且A类图书的购进数量不少于B类图书的购进数量的 ． 已知A类图书每本的售价为40元，B类图书每本的售价为58元，求如何进货才能使书店所获利润最大，最大利润为多少元？25. 如图，平面直角坐标系中，矩形OABC的对角线AC＝12，∠ACO＝30°．
(1)、求B点的坐标；(2)、把矩形沿直线DE对折使点C落在点A处，DE与AC相交于点F，求四边形ADCE的周长；(3)、若点M在坐标轴上，平面内是否存在点N，使以O、F、M、N为顶点的四边形是矩形？若存在，请直接写出点N的坐标；若不存在，请说明理由．26. 如图，Rt△ABC中，∠C＝90°，∠B＝30°， ． 点E从点A出发沿AC方向以每秒1个单位长的速度向点C匀速运动，同时点F从点B出发沿BA方向以每秒2个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D，E运动的时间是t秒（t＞0）．过点F作FD⊥BC于点D，连接DE，EF，AD．
(1)、求证：四边形AEDF是平行四边形；(2)、当t为何值时，AD⊥EF；(3)、当t为何值时，△DEF为直角三角形？请说明理由．