黑龙江省绥化市绥棱县2021-2022学年七年级下学期期末数学试题

试卷更新日期：2023-05-24 类型：期末考试

进入出卷网下载

一、单选题

1. 为了了解全校七年级300名学生的视力情况，李老师从中抽查了50名学生的视力情况．针对这个问题，下面说法正确的是（）．

A、300名学生是总体 B、每名学生是个体 C、50名学生是所抽取的一个样本 D、这个样本容量是50

查看试题解析
2. 不等式-4x≥-12的正整数解为（）．

A、1，2 B、1，2 C、1，2，3 D、0，1，2，3

查看试题解析
3. 下列四个命题：①对顶角相等；②内错角相等；③平行于同一条直线的两条直线互相平行；④如果一个角的两边分别平行于另一个角的两边，那么这两个角相等．其中真命题的个数是( )

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 如图，下列条件中，不能判断直线l₁∥l₂的是（）

A、∠1=∠3 B、∠2=∠3 C、∠4=∠5 D、∠2+∠4=180°

查看试题解析
5. 在平面直角坐标系中，将三角形各点的纵坐标都减去3，横坐标保持不变，所得图形与原图形相比 ( )

A、向右平移了3个单位 B、向左平移了3个单位 C、向上平移了3个单位 D、向下平移了3个单位

查看试题解析
6. x是(− $\sqrt{9}$ )2的平方根，y是64的立方根，则x+y=（　　）

A、3 B、7 C、3，7 D、1，7

查看试题解析
7. 下列叙述错误的是（）

A、－4是16的算术平方根 B、5是25的算术平方根 C、3是9的算术平方根 D、0.04的算术平方根是0.2

查看试题解析
8. 已知点P位于y轴右侧，距y轴3个单位长度，位于x轴上方，距离x轴4个单位长度，则点P坐标是（）

A、（3，4） B、（-3，4） C、（-4，3） D、（4，3）

查看试题解析
9. 下列说法中正确的有（）个．
①实数不是有理数就是无理数． ②无限小数都是无理数．
③无理数都是无限小数．④带根号的数都是无理数．
⑤两个无理数之和一定是无理数．

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 根据以下对话，可以求得嫒嫒所买的笔和笔记本的价格分别是（）

A、0.8元/支，2.6元/本 B、0.8元/支，3.6元/本 C、1.2元/支，2.6元/本 D、1.2元/支，3.6元/本

查看试题解析

二、填空题

11. 要使 $\sqrt{x - 4}$ 有意义，则x的取值范围是

查看试题解析
12. 在平面直角坐标系中，点 $P (- 3, 4)$ 位于.

查看试题解析
13. $\sqrt{16}$ 的算术平方根是

查看试题解析
14. 写出方程 $2 x + y = 1$ 的一个整数解．

查看试题解析
15. ∠1和∠2互余，∠2和∠3互补，∠1=63°，∠3= ．

查看试题解析
16. 如图是小刚画的一张脸，他对妹妹说“如果我用（0，2）表示左眼，用（2，2）表示右眼，那么嘴的位置可以表示成

查看试题解析
17. 若 $| x - 1 | + {(y - 2)}^{2} + \sqrt{z - 3} = 0$ ，则x+y+z=.

查看试题解析
18. 立方根是它本身的数是．

查看试题解析
19. 下列式子：3²＋4²＝5² ， 8²＋6²＝10² ， 15²＋8²＝17² ， 24²＋10²＝26²……请你利用发现的规律写出第五个等式．

查看试题解析
20. 小聪参加了一次智力竞赛，共回答了30道题，题目的评分标准是这样的：答对一题加5分，一题答错或不答倒扣1分．小聪至少要答对题才能使他的得分超过100分．

查看试题解析

三、解答题

21. 解方程组

(1)、 ${\begin{array}{l} x + 2 y = 1 ， \\ 3 x - 2 y = 11 . \end{array}$

(2)、 ${\begin{array}{l} 3 (s - t) - 2 (s + t) = 10 \\ 3 (s - t) + 2 (s + t) = 26 \end{array}$

查看试题解析
22. 解不等式组

(1)、 ${\begin{array}{l} x - 2 ＞ 0 \\ 2 (x + 1) \geq 3 x - 1 \end{array}$

(2)、 ${\begin{array}{l} x - 3 (x - 2) \geq 4 \\ \frac{2 x - 1}{5} < \frac{x + 1}{2} \end{array}$

查看试题解析
23. 在图所示的平面直角坐标系中表示下面各点．

(1)、A（0，3）， B（1，-3）， C（3，-5），D（-3，-5），E（3，5），F（5，7）

(2)、A点到原点O的距离是．

(3)、将点C向 $x$ 轴的负方向平移6个单位，它与点重合．

(4)、连接CE，则直线CE与 $y$ 轴是什么关系？

查看试题解析
24. 小王某月手机话费中的各项费用统计情况见下列图表，请你根据图表信息完成下列各题：

项目月功能费基本话费长途话费短信费

金额/元 5 50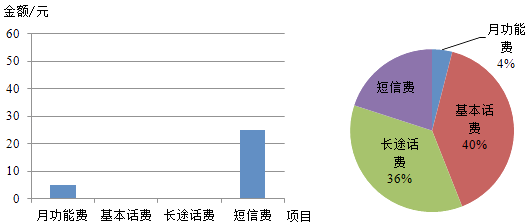

(1)、请将表格补充完整；

(2)、请将条形统计图补充完整；

(3)、扇形统计图中，表示短信费的扇形的圆心角是多少度？

查看试题解析
25. 我们知道a＋b＝0时，a³＋b³＝0也成立，若将a看成a³的立方根，b看成b³的立方根，我们能否得出这样的结论：若两个数的立方根互为相反数，则这两个数也互为相反数．

(1)、试举一个例子来判断上述猜测结论是否成立；

(2)、若 $\sqrt[3]{1 - 2 x}$ 与 $\sqrt[3]{3 x - 5}$ 互为相反数，求1－ $\sqrt{x}$ 的值．

查看试题解析
26. 如图：EF∥AD ，∠1=∠2，∠BAC=70°，将求∠AGD的过程填写完整：
因为EF∥AD，所以∠2=       ，

又因为∠1=∠2，所以∠1=∠3，

所以AB∥        ，

所以∠BAC+       =180°，

因为∠BAC=70°，所以∠AGD=       ．

查看试题解析
27. 某储运站现有甲种货物1530吨，乙种货物1150吨，安排用一列货车将这批货物运往外地，这列货车持A．B两种类型的货厢共50节．已知甲种货物35吨和乙种货物15吨可装满一节A型货厢，甲种货物25吨和乙种货物35吨可装满一节B型货厢，问：该储运站需配置A．B两种类型的货厢各几节？

查看试题解析
28. 已知直线 $l_{1} ∥ l_{2}$ ，直线l₃与直线 $l_{1}$ 、 $l_{2}$ 分别交于C、D两点．

(1)、如图①，有一动点P在线段CD之间运动（不与C、D两点重合），问在点P的运动过程中是否始终具有∠3＋∠1＝∠2这一相等关系？

(2)、如图②，当动点P在线段CD之外运动（不与C、D两点重合），问上述结论是否还成立？若不成立，试写出新的结论并说明理由．

查看试题解析

项目	月功能费	基本话费	长途话费	短信费
金额/元	5	50