黑龙江省齐齐哈尔市讷河市2021-2022学年七年级下学期期末数学试题

试卷更新日期：2023-05-24 类型：期末考试

进入出卷网下载

一、单选题

1. 2022年北京成功举办第24届冬奥会和冬残奥会，成为世界上首个“双奥之城”．本届冬残奥会会徽主体图形展示了汉字“飞”的动感和力度，如图所示在下面的四个图形中，能由如图经过平移得到的图形是（）

A、 B、 C、 D、

查看试题解析
2. π，- $\sqrt{3}$ ， 3.1416， $\sqrt[3]{8}$ 中，无理数的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 下列运算正确的是（）

A、 $\sqrt{(- 3)^{2}} = - 3$ B、 $\sqrt{81} = \pm 9$ C、 $\sqrt[3]{(- 3)^{3}} = 3$ D、 $- \sqrt[3]{27} = - 3$

查看试题解析
4. 在平面直角坐标系中，若点P（m+3，-2m）在y轴上，则m的值为（）

A、-1 B、1 C、-3 D、0

查看试题解析
5. 下列调查中，最适合采用抽样调查的是（）

A、调查某中学教职员工接种新冠疫苗的人数 B、调查中央电视台播出的重大革命历史题材电视剧《觉醒年代》的收视率 C、调查某班同学参加“学习工匠精神，向劳动者致敬”活动上传照片的数量 D、调查某校九年级学生每日体温情况

查看试题解析
6. 已知 $a < b$ ， $c$ 是有理数，下列各式中正确的是（）

A、 $a c^{2} < b c^{2}$ B、 $c - a < c - b$ C、 $a - 3 c < b - 3 c$ D、 $\frac{a}{c} < \frac{b}{c}$

查看试题解析
7. 一副直角三角板如图摆放，点F在BC的延长线上，∠B=∠DFE=90°，若DE∥BF，则∠CDF的度数为（）

A、10° B、15° C、20° D、25°

查看试题解析
8. 已知方程组 ${\begin{matrix} 2 x + y = 4 \\ x + 2 y = 5 \end{matrix}$ ，则 $x + y$ 的值为（）

A、 $- 1$ B、0 C、2 D、3

查看试题解析
9. 在抗击疫情网络知识竞赛中，为奖励成绩突出的学生，学校计划用200元购买A，B两种奖品（两种都要买），A种每个15元，B种每个25元，在钱全部用完的情况下，购买方案共有（）

A、2种 B、3种 C、4种 D、5种

查看试题解析
10. 若不等式组 ${\begin{cases} x + 8 < 4 x - 1 \\ x > m \end{cases}$ 的解集是x＞3，则m的取值范围是（）

A、m＞3 B、m≥3 C、m≤3 D、m＜3

查看试题解析

二、填空题

11. 1- $\sqrt{2}$ 的相反数是．

查看试题解析
12. 已知P（x，y）在第四象限，则Q（-x，-y+2）在第象限．

查看试题解析
13. 已知a、b为两个连续的整数，且a＜ $\sqrt{13}$ ＜b，则b-a的平方根是．

查看试题解析
14. 若点P在X轴的上方，Y轴的左侧，且到X轴的距离为3，到Y轴的距离为4，则点P的坐标是．

查看试题解析
15. 点P（m－1，2m＋1）在第二象限，则m的取值范围是

查看试题解析
16. 已知：如图，点D是射线AB上一动点，连接CD，过点D作 $D E ∥ B C$ 交直线AC于点E，若 $∠ A B C = 84 °$ ， $∠ C D E = 20 °$ ，则 $∠ A D C$ 的度数为．

查看试题解析
17. 如图，动点 $P$ 在平面直角坐标系中按图中箭头所示方向运动，第一次从原点 $O$ 运动到点 $P_{1} (1 ， 1)$ ，第二次运动到点 $P_{2} (2 ， 0)$ ，第三次运动到 $P_{3} (3 ， - 2)$ ， …，按这样的运动规律，第2022次运动后，动点 $P_{2022}$ 的坐标是．

查看试题解析

三、解答题

18.

(1)、计算： $\sqrt{25} + | 1 - \sqrt{2} | + \sqrt[3]{8} - \sqrt{{(- 3)}^{2}}$ ．

(2)、解方程组： ${\begin{array}{l} x + 2 y = 0 \\ 3 x + 4 y = 6 \end{array}$

查看试题解析
19. 解不等式组： ${\begin{array}{l} 3 (x - 2) \leq 8 - (x + 6) \\ \frac{x + 1}{2} < \frac{2 x - 1}{3} + 1 \end{array}$ ，并把解集在数轴上表示出来．

查看试题解析
20. 请根据条件进行推理，得出结论，并在括号内注明理由.
已知：如图，∠1＝∠2，∠B＋∠CDE＝180°.
求证：AB∥CD.
证明：∵∠1＝  ▲  （    ）
又∵∠1＝∠2
∴∠BFD＝∠2（    ）
∴BC∥  ▲  （   ）
∴∠C＋  ▲  ＝180°（    ）
又∵∠B＋∠CDE＝180°
∴∠B＝∠C
∴AB∥CD（   ）.

查看试题解析
21. 如图，三角形ABC的三个顶点坐标为A（-2，0），B（2，-1），C（1，2），将这个三角形向右平移1个单位长度，再向上平移2个单位长度，得三角形 $A^{'} B^{'} C^{'}$ ，点 $A^{'}$ ， $B^{'}$ ， $C^{'}$ 分别是平移后点A，B，C的对应点．

(1)、画出平移后的三角形 $A^{'} B^{'} C^{'}$ ，写出坐标 $B^{'}$ （） $C^{'}$ （）

(2)、求三角形ABC的面积

(3)、在x轴上是否存在一点P，使三角形OCP的面积等于三角形ABC面积的2倍，若存在，请直接写出P点坐标，若不存在，请说明理由．

查看试题解析
22. 某校为了解疫情期间学生在家上网课的学习情况，随机抽取了该校部分学生对其学习效果进行调查，根据相关数据，绘制成如图不完整的统计图．

(1)、此次调查的样本容量为，学习效果“较差”的部分对应的圆心角度数为；

(2)、补全条形图；

(3)、请估计该校3000名学生疫情期间网课学习效果“一般”的学生人数．

查看试题解析
23. 已知 $A B / / C D$ ，点M为直线AC上的动点（点M不与点A，C重合）， $M E ⊥ A C$ 交直线CD于E．

(1)、如图1，当点M在CA上时，若 $∠ M A B = 46 °$ ，则 $∠ M E C =$ ；

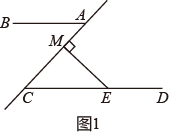(2)、如图2，当点M在CA的延长线上时， $∠ M A B$ 与 $∠ M E C$ 有怎样的数量关系？写出结论，并说明理由；

(3)、当点M在AC的延长线上时， $∠ M A B$ 与 $∠ M E C$ 有怎样的数量关系？请直按写出结论．

查看试题解析
24. 全国上下疫情防控工作仍处于“逆水行舟、不进则退”的关键时期，我县各学校坚持做好疫情防控的各项工作，测温就是其中重要的一项．为方便师生测体温某学校计划购买甲、乙两种额温枪．经调研得知：购买1个甲种额温枪和2个乙种额温枪共需700元，购买2个甲种额温枪和3个乙种额温枪共需1160元．

(1)、求每个甲种额温枪和乙种额温枪各多少元；

(2)、该学校准备购买甲、乙两种型号的额温枪共50个；要求总费用不超过11750元，其中购买甲种额温枪不超过15个．请问：学校有哪几种购买方案？

查看试题解析