黑龙江省齐齐哈尔市梅里斯达斡尔族区2021-2022学年七年级下学期期末考试数学试题

试卷更新日期：2023-05-24 类型：期末考试

进入出卷网下载

一、单选题

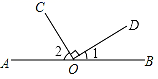
1. 下列调查活动中适合使用全面调查的是（）

A、“奔跑吧，兄弟”节目的收视率 B、“神舟十一号”飞船的零件合格率 C、某种品牌节能灯的使用寿命 D、全国植树节中栽植树苗的成活率

查看试题解析
2. 如图，点O为直线AB上一点，OC⊥OD．如果∠1=35°，那么∠2的度数是（）

A、35° B、45° C、55° D、65°

查看试题解析
3. 已知 ${\begin{array}{l} x = 2, \\ y = 1 \end{array}$ 是二元一次方程组 ${\begin{array}{l} a x + b y = 7, \\ a x - b y = 1 \end{array}$ 的解，则 $a - b$ 的值为（）

A、－1 B、1 C、2 D、3

查看试题解析
4. 在平面直角坐标系中，已知x轴上的点P到y轴的距离为3，则点P的坐标为（）

A、（3，0） B、（0，3）或（0，-3） C、（0，3） D、（3，0）或（-3，0）

查看试题解析
5. 如图，下列条件中，不能判断直线l₁∥l₂的是（）

A、∠1=∠3 B、∠2=∠3 C、∠4=∠5 D、∠2+∠4=180°

查看试题解析
6. 若点P（3﹣m，m﹣1）在第二象限，则m的取值范围是（）

A、m＞3 B、m＜1 C、m＞1 D、1＜m＜3

查看试题解析
7. 为了奖励疫情期间线上学习表现优异的同学，某校决定用1200元购买篮球和排球，其中篮球每个120元，排球每个90元，在两种球类都购买且资金恰好用尽的情况下，购买方案有（）

A、2种 B、3种 C、4种 D、5种

查看试题解析
8. 下列四个命题：①对顶角相等；②内错角相等；③平行于同一条直线的两条直线互相平行；④如果一个角的两边分别平行于另一个角的两边，那么这两个角相等．其中真命题的个数是( )

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 鸡兔同笼问题是我国古代著名趣题之一，大约在 1500 年前，《孙子算经》中就记载了这个有趣的问题．书中是这样叙述的：“今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？”这四句话的意思是：有若干只鸡、兔同在一个笼子里，从上上面数，有 35 个头；从下面数，有 94 只脚．求笼中各有几只鸡和兔？经计算可得（）

A、鸡 20 只，兔 15 只 B、鸡 12 只，兔 23 只 C、鸡 15 只，兔 20 只 D、鸡 23 只，兔 12 只

查看试题解析
10. 对任意两个实数a、b定义两种运算：a▲b= ${\begin{array}{l} a (a \geq b ） \\ b (a < b) \end{array}$ ， a▼b= ${\begin{array}{l} b (a \geq b ） \\ a (a < b) \end{array}$ 并且定义运算顺序仍然是先做括号内的，例如（-2）▲3=3、（-2）▼3=-2、（（-2）▲3））▼2=2，那么（ $\sqrt{5}$ ▲2）▼ $\sqrt[3]{27}$ 等于（）

A、 $\sqrt{5}$ B、3 C、6 D、3 $\sqrt{5}$

查看试题解析

二、填空题

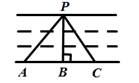
11. 请写出三个无理数：．

查看试题解析
12. 若 $\sqrt{2 x + 3}$ 在实数范围内有意义，则实数 $x$ 的取值范围是．

查看试题解析
13. 如图，要在河的两岸搭建一座桥，在PA，PB，PC三种搭建方式中，最短的是PB，其理由是．

查看试题解析
14. 如图，BA⊥FC于A点，过A点作DE $∥$ BC，若∠EAF=125°，则∠B= ．

查看试题解析
15. 若 $3 a - 2$ 和 $2 a - 3$ 都是一个正数的不相等的平方根，则这个正数是．

查看试题解析
16. 如图，在平面直角坐标系中， $A (- 2 ， 0)$ ，将点 $A$ 向下平移1个单位，再向右平移2个单位得到点 $B$ ，若点 $C$ 在 $y$ 轴上，且 $S_{△ A B C} = 3$ ，则点 $C$ 的坐标为．

查看试题解析
17. 如图，一个动点P在平面直角坐标系中按箭头所示的方向做折线运动，即第一次从原点运动到（1，1），第二次从（1，1）运动到（2，0），第三次从（2，0）运动到（3，2），第四次从（3，2）运动到（4，0），第五次从（4，0）运动到（5，1）……按照这样的运动规律，经过第2022次运动后，动点P的坐标为．

查看试题解析

三、解答题

18. 计算

(1)、 $\sqrt{\frac{49}{16}} + \sqrt{{(- 5)}^{2}} \div \sqrt[3]{- 64}$

(2)、 $| \sqrt{3} - 2 | - | \sqrt{5} - \sqrt{3} | + 3 (2 - \sqrt{5})$

查看试题解析
19. 解方程组

(1)、 ${\begin{array}{l} x = 3 + y \\ 3 x - 2 y = 5 \end{array}$

(2)、 ${\begin{array}{l} 5 x + 2 y = 2 \\ 3 x + 4 y = - 3 \end{array}$

查看试题解析
20. 解不等式组： ${\begin{array}{l} 4 x > 2 x - 6 \\ \frac{x + 1}{3} \geq x - 1 \end{array}$ ，把解集表示在数轴上，并写出所有整数解．

查看试题解析
21. 完成下面的证明．
已知：如图，BC∥DE，BE、DF分别是∠ABC、∠ADE的平分线．

求证：∠1＝∠2．

证明：∵BC∥DE，

∴∠ABC＝∠ADE（  ）．

∵BE、DF分别是∠ABC、∠ADE的平分线．

∴∠3＝ $\frac{1}{2}$ ∠ABC，∠4＝ $\frac{1}{2}$ ∠ADE．

∴∠3＝∠4．

∴  ▲   ∥  ▲  （  ）．

∴∠1＝∠2（  ）．

查看试题解析
22. 张强和李毅二人分别从相距20千米的A、B两地出发，相向而行，如果张强比李毅早出发30分钟，那么在李毅出发后2小时，他们相遇；如果他们同时出发，那么1小时后两人还相距11千米．求张强、李毅每小时各走多少千米．

查看试题解析
23. 为了创设全新的校园文化氛围，进一步组织学生开展课外阅读，让学生在丰富多彩的书海中，扩大知识源，亲近母语，提高文学素养．某校准备开展“与经典为友、与名著为伴”的阅读活动，活动前对本校学生进行了“你最喜欢的图书类型（只写一项）”的随机抽样调查，相关数据统计如下：

请根据以上信息解答下列问题：

(1)、该校对名学生进行了抽样调查．

(2)、请将图1和图2补充完整；

(3)、已知该校共有学生1800人，利用样本数据估计全校学生中最喜欢小说的人数约为多少人？

查看试题解析
24. 课题学习：平行线的“等角转化”功能．
阅读理解：

如图1，已知点A是BC外一点，连接AB、AC．求∠BAC+∠B+∠C的度数．

解：过点A作DE $∥$ BC．

∵DE $∥$ BC，

∴∠B=∠EAB，∠C=∠DAC．

又∵∠EAB+∠BAC+∠DAC=180°，

∴∠BAC+∠B+∠C=180°．

(1)、解题反思：从上面的推理过程中，我们发现平行线具有的功能．

(2)、方法运用：
如图2，已知AB $∥$ DE，试说明：∠D+∠BCD-∠B=180°．（提示：过点C作CF $∥$ AB）

(3)、解决问题：
如图3，将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边重合，含30°角的直角三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1=度．

(4)、【拓展发现】
①如图4，若AB $∥$ DE，∠B、∠C、∠D有怎样的关系：；

②如图5，若AB $∥$ DE，∠B、∠C、∠D有怎样的关系：．

查看试题解析