黑龙江省牡丹江市林口县2021-2022学年七年级下学期期末考试数学试题
试卷更新日期:2023-05-24 类型:期末考试
一、填空题
-
1. 已知=2.8,若=280,则= .2. 若点P(m+3,m+2)在x轴上,则点P的坐标为 .3. 下列调查中,适宜采用全面调查(普查)方式的是 .
①对我国自行研制的大型飞机C919各零部件质量情况的调查;②对某个工厂口罩质量的调查;③对疫情后某班学生心理健康状况的调查.
4. A,B两地相距80km.一艘船从A出发,顺水航行4h到B,而从B出发逆水航行5h到A,已知船顺水航行、逆水航行的速度分别是船在静水中的速度与水流速度的和与差,求船在静水中的速度和水流速度.设船在静水中的速度为x千米/小时,水流速度为y千米/小时,则可列方程组为 .5. 若 , 那么(填“>”“<”或“=”).6. 如图,直线AB、CD相交于点O,∠COE是直角,OF平分∠AOD,若∠BOE=42°,则∠AOF的度数是.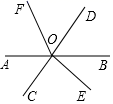 7. 点O在直线AB上,过点O作射线OC、OD,使得 , 若 , 则的度数是 .8. 若不等式组的整数解共有三个,则a的取值范围是 .
7. 点O在直线AB上,过点O作射线OC、OD,使得 , 若 , 则的度数是 .8. 若不等式组的整数解共有三个,则a的取值范围是 .二、单选题
-
9. 下面四个图形中,∠1=∠2一定成立的是( )A、
 B、
B、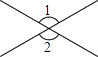 C、
C、 D、
D、 10. 如图,表示 的点在数轴上表示时,所在哪两个字母之间( )
10. 如图,表示 的点在数轴上表示时,所在哪两个字母之间( ) A、C与D B、A与B C、A与C D、B与C11. 下列命题中,是真命题的是( )A、无限小数都是无理数 B、若 ,则 C、 轴上的点,纵坐标为0 D、过一点有且只有一条直线与已知直线平行12. 佳佳学习小组为了解本地区大约有多少成年人吸烟,随机调查了100个成年人,结果其中有25个成年人吸烟.对于这个数据收集与处理的问题,下列说法正确的是( )A、调查的方式是普查 B、样本容量是25人 C、样本是100个成年人 D、本地区约有25%的成年人吸烟13. 如图,在平面直角坐标系中,的顶点 , 的坐标分别为 , , 把沿轴向右平移得到 , 如果点的坐标为 , 则点的坐标为( )
A、C与D B、A与B C、A与C D、B与C11. 下列命题中,是真命题的是( )A、无限小数都是无理数 B、若 ,则 C、 轴上的点,纵坐标为0 D、过一点有且只有一条直线与已知直线平行12. 佳佳学习小组为了解本地区大约有多少成年人吸烟,随机调查了100个成年人,结果其中有25个成年人吸烟.对于这个数据收集与处理的问题,下列说法正确的是( )A、调查的方式是普查 B、样本容量是25人 C、样本是100个成年人 D、本地区约有25%的成年人吸烟13. 如图,在平面直角坐标系中,的顶点 , 的坐标分别为 , , 把沿轴向右平移得到 , 如果点的坐标为 , 则点的坐标为( ) A、 B、 C、 D、14. 已知点M(1-2m,m-1)在第四象限内,那么m的取值范围是( )A、m>1 B、m< C、<m<1 D、m<或m>115. 如图,下列条件中,不能判断直线的是( )
A、 B、 C、 D、14. 已知点M(1-2m,m-1)在第四象限内,那么m的取值范围是( )A、m>1 B、m< C、<m<1 D、m<或m>115. 如图,下列条件中,不能判断直线的是( ) A、 B、 C、 D、16. 《九章算术》中记载“今有共买羊,人出五,不足四十五;人出七,不足三,问人数、羊价各几何?”其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,还差3钱,问合伙人数、羊价各是多少?此问题中人数为( )A、21 B、155 C、150 D、2017. 已知平面内不同的两点A(a+2,4)和B(3,2a+2)到x轴的距离相等,则a的值为( )A、﹣3 B、﹣5 C、1或﹣3 D、1或﹣518. 实数a,b,c,d在数轴上的位置如图所示,下列关系式不正确的是( )
A、 B、 C、 D、16. 《九章算术》中记载“今有共买羊,人出五,不足四十五;人出七,不足三,问人数、羊价各几何?”其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,还差3钱,问合伙人数、羊价各是多少?此问题中人数为( )A、21 B、155 C、150 D、2017. 已知平面内不同的两点A(a+2,4)和B(3,2a+2)到x轴的距离相等,则a的值为( )A、﹣3 B、﹣5 C、1或﹣3 D、1或﹣518. 实数a,b,c,d在数轴上的位置如图所示,下列关系式不正确的是( ) A、|a|>|b| B、c+d>0 C、b<d D、b-a<019. 以方程组的解为坐标的点(x,y)在第( )象限.A、第一象限 B、第二象限 C、第三象限 D、第四象限20. 一张长方形纸条按如图所示折叠,EF是折痕,若∠EFB=35°,则:①∠GEF=35°;②∠EGB=70°;③∠AEG=110°;④=70°.以上结论正确的有( )
A、|a|>|b| B、c+d>0 C、b<d D、b-a<019. 以方程组的解为坐标的点(x,y)在第( )象限.A、第一象限 B、第二象限 C、第三象限 D、第四象限20. 一张长方形纸条按如图所示折叠,EF是折痕,若∠EFB=35°,则:①∠GEF=35°;②∠EGB=70°;③∠AEG=110°;④=70°.以上结论正确的有( )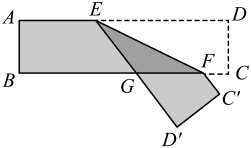 A、① ② ③ ④ B、② ③ ④ C、① ② ③ D、① ②
A、① ② ③ ④ B、② ③ ④ C、① ② ③ D、① ②三、解答题
-
21.(1)、计算:(2)、解方程组:(3)、解不等式组 并把不等式组的解集在数轴上表示出来.22. 已知直线AB∥CD,P为平面内一点,连接PA、PD.
 (1)、如图1,已知∠A=50°,∠D=150°,求∠APD的度数;(2)、如图2,判断∠PAB、∠CDP、∠APD之间的数量关系为 .23. 随着社会的发展,通过微信朋友圈发布自己每天行走的步数已经成为一种时尚.“健身达人”小陈为了了解他的好友的运动情况.随机抽取了部分好友进行调查,把他们6月1日那天行走的情况分为四个类别:A(0~5000步)(说明:“0~5000”表示大于等于0,小于等于5000,下同),B(5001~10000步),C(10001~15000步),D(15000步以上),统计结果如图所示:
(1)、如图1,已知∠A=50°,∠D=150°,求∠APD的度数;(2)、如图2,判断∠PAB、∠CDP、∠APD之间的数量关系为 .23. 随着社会的发展,通过微信朋友圈发布自己每天行走的步数已经成为一种时尚.“健身达人”小陈为了了解他的好友的运动情况.随机抽取了部分好友进行调查,把他们6月1日那天行走的情况分为四个类别:A(0~5000步)(说明:“0~5000”表示大于等于0,小于等于5000,下同),B(5001~10000步),C(10001~15000步),D(15000步以上),统计结果如图所示: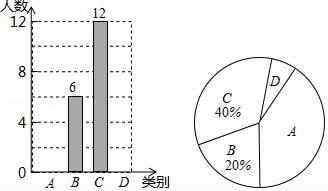
请依据统计结果回答下列问题:
(1)、本次调查中,一共调查了位好友.(2)、已知A类好友人数是D类好友人数的5倍.①请补全条形图;
②扇形图中,“A”对应扇形的圆心角为 ▲ 度.
③若小陈微信朋友圈共有好友150人,请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步?
24. 已知,在平面直角坐标系中,三角形ABC三个顶点的坐标分别为 , , .请在所给的平面直角坐标系中按要求完成以下问题: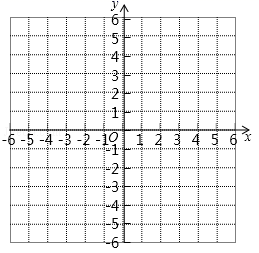 (1)、画出三角形ABC;(2)、将三角形ABC先向下平移6个单位长度,再向左平移3个单位长度后得到的三角形 (点 , , 分别是点A,B,C移动后的对应点)请画出三角形 ;并判断线段AC与 位置与数量关系.25. 星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
(1)、画出三角形ABC;(2)、将三角形ABC先向下平移6个单位长度,再向左平移3个单位长度后得到的三角形 (点 , , 分别是点A,B,C移动后的对应点)请画出三角形 ;并判断线段AC与 位置与数量关系.25. 星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:进价(元/个)
售价(元/个)
电饭煲
200
250
电压锅
160
200
(1)、一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?(2)、为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50个,且电饭煲的数量不少于23个,问橱具店有哪几种进货方案?并说明理由;(3)、在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?26. 如图在直角坐标系中,已知A(0,a),B(b,0),C(3,c)三点,若a,b,c满足关系式:=0. (1)、求a,b,c的值.(2)、求△ABC的面积.(3)、是否存在点P(x,2x),使△BCP的面积为△AOB的面积的两倍?若存在,直接写出点P的坐标,若不存在,请说明理由.
(1)、求a,b,c的值.(2)、求△ABC的面积.(3)、是否存在点P(x,2x),使△BCP的面积为△AOB的面积的两倍?若存在,直接写出点P的坐标,若不存在,请说明理由.