黑龙江省哈尔滨市道里区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2023-05-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程中，属于二元一次方程的是（）

A、 $x - y = z$ B、 $2 x y - 1 = 0$ C、 $x^{2} + 2 x + 1 = 0$ D、 $x = 2 y$

查看试题解析
2. 已知 $a < b$ ，则下列不等式中正确的是（）

A、 $2 a > 2 b$ B、 $- a < - b$ C、 $a + 6 < b + 6$ D、 $1 - a < 1 - b$

查看试题解析
3. 在下列长度的木棒中，能与4cm、9cm长的两根木棒钉成一个三角形的是（）

A、 $3 c m$ B、 $4 c m$ C、 $5 c m$ D、 $6 c m$

查看试题解析
4. 在 $△ A B C$ 中，若 $∠ A = ∠ B + ∠ C$ ，那么 $△ A B C$ 的形状为（）．

A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定

查看试题解析
5. 下列四个图形中，线段 $B E$ 是 $△ A B C$ 中 $A C$ 边上的高的图形是（）

A、 B、 C、 D、

查看试题解析
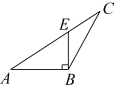6. 下列图形中具有稳定性的是（）.

A、三角形 B、长方形 C、正方形 D、平行四边形

查看试题解析
7. 某班共有六个学习合作小组人数如下（单位：人）：5，6，7，7，7，8，那么这组数据的众数为（）人．

A、5 B、6 C、7 D、8

查看试题解析
8. 若点 $P (1 - m ， m)$ 在第二象限，则m的取值范围（）．

A、 $m > 0$ B、 $m < 1$ C、 $m > 1$ D、 $0 < m < 1$

查看试题解析
9. 如果等腰三角形的两边长分别为2和5，则它的周长为( )

A、9 B、7 C、12 D、9或12

查看试题解析
10. 下列命题中真命题的个数为（）
①直角三角形两个锐角互余；②外角和等于360°的多边形一定是四边形；③有两边和一角相等的两个三角形一定全等；④角平分线上的点到角两边的距离相等．

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 把二元一次方程 $2 x - y = 6$ 化成用含x的式子表示y的形式，则 $y =$ ．

查看试题解析
12. 把“x的5倍与7的差不大于3”表示为．

查看试题解析
13. 已知 ${\begin{array}{l} x = 2 \\ y = - 1 \end{array}$ 是方程 $m x - y = 3$ 的解，则m的值是．

查看试题解析
14. 一个多边形每个内角都等于120°，则它的边数为．

查看试题解析
15. 如图，在 $△ A B C$ 中， $A D ⊥ B C$ 于点D， $∠ B = ∠ B A D$ ， $∠ B A C = 70 °$ ，则 $∠ D A C$ 的度数为．

查看试题解析
16. 不等式组 ${\begin{array}{l} x \geq - 2 \\ x < 0 \end{array}$ 的整数解为．

查看试题解析
17. 某校男子足球队的年龄分布如条形图所示，则这些队员年龄的中位数是．

查看试题解析
18. 若 ${\begin{array}{l} m + n = - 2 \\ m - 2 n = 1 \end{array}$ ，则 $2 m - n$ 的值为．

查看试题解析
19. 在 $△ A B C$ 中， $∠ A B C = 40 °$ ， $∠ A C B = 20 °$ ，点D在 $B C$ 边上，连接 $A D$ ，若 $△ A B D$ 为直角三角形，则 $∠ D A C$ 的度数为．

查看试题解析
20. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，点D为 $A C$ 边上一点， $E D ⊥ A C$ ， $C E ⊥ A B$ ， $A B = C E$ ，若 $B C = 2$ ， $D E = 5$ ，则线段 $A D$ 的长为．

查看试题解析

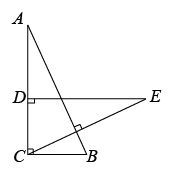
三、解答题

21. 解方程组：

(1)、 ${\begin{array}{l} 2 x + y = 4 \\ x - y = - 1 \end{array}$

(2)、 ${\begin{array}{l} 2 m - 5 n = - 3 \\ - 4 m + n = - 3 \end{array}$

查看试题解析
22. 如图， $△ A B C$ 在 $8 \times 8$ 的网格中，每一个小格都是边长为1的正方形， $△ A B C$ 的顶点均在格点上．

(1)、画出 $△ A B C$ 的中线 $B D$ ；

(2)、画出 $A B$ 边上的高 $C E$ ；

(3)、直接写出 $△ A B C$ 的面积．

查看试题解析
23. 解不等式（组）并把解集表示在数轴上：

(1)、 $2 (x + 5) ≤ 3 (x - 5)$

(2)、 ${\begin{array}{l} \frac{1}{2} (x + 1) < 2 \\ \frac{x + 2}{2} \geq \frac{x + 3}{3} \end{array}$

查看试题解析
24. 已知： $A B = C D$ ， $A F ⊥ B C$ ， $D E ⊥ B C$ .垂足分别为F、E， $C F = B E$ ．

(1)、如图，求证： $∠ A = ∠ D$ ；

(2)、如图，连接 $A C$ 、 $A E$ 、 $B D$ ，若 $C E = 2 B E$ ，在不添加任何辅助线的情况下，请直接写出四个三角形，使每一个三角形的面积都等于 $△ D C E$ 面积的一半．

查看试题解析
25. 某商场准备从厂家选购甲、乙两种商品，乙种商品每件进价比甲种商品每件进价少20元，已知购进5件甲种商品和4件乙种商品共需要1000元．

(1)、求甲、乙两种商品每件的进价分别是多少元？

(2)、若甲种商品的售价为每件145元，乙种商品的售价为每件120元，该商场准备购进甲、乙两种商品共40件，且这两种商品全部售出后总利润不少于920元，则乙种商品最多可购进多少件？

查看试题解析
26. 已知：在 $△ A B C$ 中， $C D ⊥ A B$ 于点D， $B E ⊥ A C$ 于点E， $C D$ 与 $B E$ 交于点G．

(1)、如图，求证： $∠ A B E = ∠ A C D$ ；

(2)、如图，若 $A D = D G$ ，求证： $B G = A C$ ；

(3)、如图，在（2）的条件下，连接 $D E$ ，若 $D E = 6$ ，求四边形 $A D G E$ 的面积．

查看试题解析
27. 如图，在平面直角坐标系中，点O为坐标原点，点 $B (m ， n)$ 在第一象限， $B A ⊥ x$ 轴于点A， $B C ⊥ y$ 轴于点C，且m、n满足方程组 ${\begin{array}{l} m + n = 40 \\ 2 m - n = 20 \end{array}$ ．

(1)、点B的坐标为；

(2)、点D、E分别在线段 $C B$ 、 $O C$ 上， $A E ⊥ O D$ 于点H，设线段 $C E$ 的长为t，请用含t的式子表示线段 $C D$ 的长；

(3)、在（2）的条件下，若 $E H ： H A = 9 ： 16$ ，四边形 $C E H D$ 的面积为96，求点H的坐标．

查看试题解析