黑龙江省大庆市龙凤区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2023-05-24 类型：期末考试

进入出卷网下载

一、单选题

1. 在下列实数中：0， $\sqrt{2.5}$ ， $- 3.1415$ ， $\sqrt{4}$ ， $\frac{22}{7}$ ，0.343343334…无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{9} = \pm 3$ B、 $\sqrt[3]{- 8} = 2$ C、 ${(\sqrt{5})}^{2} = \sqrt{5}$ D、 $\sqrt{2^{2}} = 2$

查看试题解析
3. 下列命题是假命题的是（）

A、平方根等于本身的实数只有0； B、两直线平行，内错角相等； C、点P（2，－5）到x轴的距离为5； D、数轴上没有点表示π这个无理数．

查看试题解析
4. 当 $m$ 为何值时，函数 $y = (m - 3) x^{3 - | m |} + m + 2$ 是一次函数（）

A、2 B、－2 C、－2和2 D、3

查看试题解析
5. 已知点 $(- 4 ， y_{1})$ ， $(2 ， y_{2})$ 都在直线 $y = - \frac{1}{2} x + 2$ 上，则 $y_{1}$ ， $y_{2}$ 大小关系是（）

A、 $y_{1} = y_{2}$ B、 $y_{1} > y_{2}$ C、 $y_{1} < y_{2}$ D、不能比较

查看试题解析
6. 已知：点A（m-1，3）与点B（2，n-1）关于 $x$ 轴对称，则 ${(m + n)}^{2022}$ 的值为（）

A、0 B、1 C、－1 D、201

查看试题解析
7. 如图，在平面直角坐标系中，直线l₁： $y = x + 3$ 与直线l₂： $y = m x + n$ 交于点A（ $- 1$ ，b），则关于x、y的方程组 ${\begin{array}{l} y = x + 3 \\ y = m x + n \end{array}$ 的解为（）

A、 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = - 1 \end{array}$ C、 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ D、 ${\begin{array}{l} x = - 1 \\ y = - 2 \end{array}$

查看试题解析
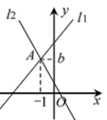8. 在同一直角坐标系中，一次函数y＝kx+b和y＝bx+k的图象可能正确的是（）

A、 B、 C、 D、

查看试题解析
9. 八块相同的长方形地砖拼成一个长方形，每块长方形地砖的长等于（）

A、 $15 c m$ B、 $30 c m$ C、 $40 c m$ D、 $45 c m$

查看试题解析
10. 如图中的图象（折线ABCDE）描述了一汽车在某一直道上的行驶过程中，汽车离出发地的距离s（千米）和行驶时间t（小时）之间的函数关系．根据图中提供的信息，给出下列说法：
①汽车共行驶了120千米；

②汽车在行驶途中停留了0.5小时；

③汽车在整个行驶过程中的平均速度为 $\frac{160}{3}$ 千米/时；

④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少．

其中正确的说法有（　　）

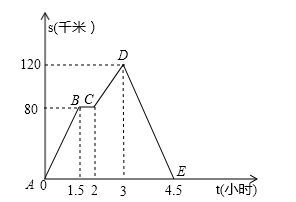A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. $\sqrt{81}$ 的平方根是．

查看试题解析
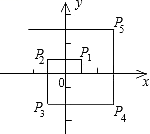
12. 把“对顶角相等”改写成“如果...那么...”的形式是：．

查看试题解析
13. 在函数 $y = \frac{\sqrt{x - 1}}{x^{2} - 1}$ 中，自变量的取值范围是．

查看试题解析
14. 已知直角三角形两边长分别为4和5，则第三边长为．

查看试题解析
15. 在平面直角坐标系中，已知点M（m-1，2m+3），点N（-3，2），且直线MN $∥$ y轴，求线段MN的长．

查看试题解析
16. 已知 $4 x^{2} + y^{2} - 4 x - 6 y + 10 = 0$ ，则 $2 x y$ 的平方根为．

查看试题解析
17. 如图，在直角坐标系中，设动点M自 $P_{0} (1 ， 0)$ 处向上运动1个单位至 $P_{1} (1 ， 1) ，$ 然后向左运动2个单位至 $P_{2}$ 处，再向下运动3个单位至 $P_{3}$ 处，再向右运动4个单位至 $P_{4}$ 处，再向上运动5个单位至 $P_{5}$ 处，……，如此继续运动下去，设 $P_{n} (x_{n} ， y_{n}) ， n = 1 ， 2 ， 3 ，$ ……，则 $x_{1} + x_{2} + x_{3} + \dots + x_{99} + x_{100} =$ .

查看试题解析
18. 如图， $△ A B C$ 中， $∠ A = 45 °$ ， $A B = 3$ ， $A C = 2 \sqrt{2}$ ，若点 $D$ 、 $E$ 、 $F$ 分别是三边 $A B$ 、 $B C$ 、 $C A$ 上的动点，则 $△ D E F$ 周长的最小值为．

查看试题解析

三、解答题

19. 计算题

(1)、 $\frac{\sqrt{3}}{3 + \sqrt{3}} + (\sqrt{2} + 1)^{0} + \sqrt{\frac{2}{3}} \times \sqrt{\frac{3}{8}}$ ；

(2)、 ${\begin{array}{l} x - 4 (y - \frac{1}{4}) = 3 \\ \frac{x}{2} - \frac{y}{3} = 1 \end{array}$ ．

查看试题解析
20. 如图所示的方格纸中，每个小方格的边长都是 $1$ ，点 $A (- 4 ， 1)$ ， $B (- 3 ， 3)$ ， $C (- 1 ， 2)$ ．

(1)、作 $△ A B C$ 关于y轴对称的 $△ A^{'} B^{'} C^{'}$ ；

(2)、通过作图在x轴上找出点P，使 $P A + P C$ 最小，并直接写出点P的坐标．

查看试题解析
21. 如图，已知长方形 $A B C D$ 中 $A B = 8 c m ， B C = 10 c m$ ，在边 $C D$ 上取一点E，将 $△ A D E$ 折叠使点D恰好落在 $B C$ 边上的点F，求 $C E$ 的长．

查看试题解析
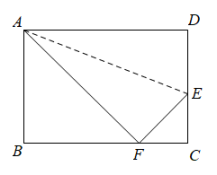22. 如图，直线 $a$ 经过点A（1，6）和点B（-3，-2）．

(1)、求直线 $a$ 的函数表达式；

(2)、求 $△ A B O$ 的面积．

查看试题解析

23. 某校举办了国学知识竞赛，满分10分，学生得分均为整数．在初赛中，甲乙两组（每组10人）学生成绩如下（单位：分）

甲组：3，6，6，6，6，6，7，9，9，10

乙组：5，6，6，6，7，7，7，7，8，9

组别	平均数	中位数	众数	方差
甲组	6.8	a	6	3.76
乙组	b	7	c	1.16

(1)、以上成绩统计分析表中a＝， b＝，c＝；

(2)、小明同学说：“这次竞赛我得了7分，在我们小组中属中游略偏上！”观察上面表格判断，小明可能是组的学生；

(3)、从平均数和方差看，若从甲乙两组学生中选择一个组参加决赛，应选哪个组？并说明理由．

查看试题解析

24. 甲、乙两车分别从BA两地同时出发，甲车匀速前往A地，乙车匀速前往B地，到达B地立即以另一速度按原路匀速返回到A地，设甲、乙两车离A地的路程为y（千米），乙车行驶的时间为x（时），y与x之间的函数图象如图所示．

(1)、乙车从A地到达B地的速度是千米/时；

(2)、乙车到达B地时甲车距A地的路程是千米；

(3)、m=；n= ．

查看试题解析
25. 如图，四边形 $A B C D$ 中，AD//BC， $∠ A = ∠ D = 90 °$ ，点 $E$ 是 $A D$ 的中点，连接 $B E$ ，将 $△ A B E$ 沿 $B E$ 折叠后得到 $△ G B E$ ，且点 $G$ 在四边形 $A B C D$ 内部，延长 $B G$ 交 $D C$ 于点 $F$ ，连接 $E F$ ．且 $G F = D F$ ．

(1)、求证： $△ E G F ≌ △ E D F$ ；

(2)、求证： $B G = C D$ ；

(3)、若点 $F$ 是 $C D$ 的中点， $B C = 8$ ，求 $C D$ 的长．

查看试题解析
26. 某景点的门票价格如下表:

购票人数（人）

1~50

51~99

100以上（含100）

门票单价（元）

48

45

42

(1)、某校七年级1、2两个班共有102 人去游览该景点，其中1班人数少于50人，2班人数多于50人且少于100人．如果两班都以班为单位单独购票，则一共支付4737 元，两个班各有多少名学生？

(2)、该校八、九年级自愿报名浏览该景点，其中八年级的报名人数不超过50人，九年级的报名人数超过50人，但不超过80人．若两个年级分别购票，总计支付门票费4914元；若合在一起作为一个团体购票，总计支付门票费4452元，问八年级、九年级各报名多少人？

查看试题解析
27. 观察下列式子变形过程，完成下列任务：
$\sqrt{1 + \frac{1}{n^{2}} + \frac{1}{{(n + 1)}^{2}}} = \sqrt{{(1 + \frac{1}{n})}^{2} - \frac{2}{n} + \frac{1}{{(n + 1)}^{2}}}$

$= \sqrt{{(\frac{n + 1}{n})}^{2} - 2 \frac{n + 1}{n} \cdot \frac{1}{n + 1} + \frac{1}{{(n + 1)}^{2}}}$

$= \sqrt{{(\frac{n + 1}{n} - \frac{1}{n + 1})}^{2}} = \frac{n + 1}{n} - \frac{1}{n + 1}$

$= 1 + \frac{1}{n} - \frac{1}{n + 1}$

(1)、类比上述变形过程的基本思路，猜想 $\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}}$ 的结果并验证；

(2)、计算： $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} + \sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} + \sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} + ⋯ + \sqrt{1 + \frac{1}{9 9^{2}} + \frac{1}{10 0^{2}}}$ .

查看试题解析
28. 如图，将一张边长为8的正方形纸片 $O A B C$ 放在直角坐标系中，使得 $O A$ 与 $y$ 轴重合， $O C$ 与 $x$ 轴重合，点 $P$ 为正方形 $A B$ 边上的一点（不与点 $A$ 、点 $B$ 重合）．将正方形纸片折叠，使点 $O$ 落在 $P$ 处，点 $C$ 落在 $G$ 处， $P G$ 交 $B C$ 于 $H$ ，折痕为 $E F$ ．连接 $O P$ 、 $O H$ ．

(1)、初步探究：当 $A P = 4$ 时，①直接写出点 $E$ 的坐标 ▲ ；②求直线 $E F$ 的函数表达式．

(2)、深入探究：当点 $P$ 在边 $A B$ 上移动时， $∠ A P O$ 与 $∠ O P H$ 的度数总是相等，请说明理由．

(3)、拓展应用：当点 $P$ 在边 $A B$ 上移动时， $△ P B H$ 的周长是否发生变化？并证明你的结论．

查看试题解析

购票人数（人）	1~50	51~99	100以上（含100）
门票单价（元）	48	45	42