安徽省宿州市萧县2021-2022学年七年级下学期期末数学试题
试卷更新日期:2023-05-24 类型:期末考试
一、单选题
-
1. 2021年3月20日三星堆遗址的最新考古发现又一次让世界为之瞩目,下列三星堆文物图案中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下面运算中,正确的是( )A、 B、 C、 D、3. 英国曼彻斯特大学的两位科学家因为成功地从石墨中分离出石墨烯,荣获了诺贝尔物理学奖,石墨烯的理论厚度仅0.000 000 000 34米,将这个数用科学记数法表示为( )A、0.34×10-9 B、3.4×10-9 C、3.4×10-10 D、3.4×10-114. 以下说法正确的是( )A、在367人中至少有两个人的生日相同 B、一次摸奖活动的中奖率是1%,那么摸100次必然会中一次奖 C、一副扑克牌中,随意抽取一张是红桃K,这是必然事件 D、一个不透明的袋中装有3个红球,5个白球,搅匀从中任意摸出一个球,摸到红球的可能性大于摸到白球的可能性5. 如图,于点C,连接 , 若 , 则的度数为( )
2. 下面运算中,正确的是( )A、 B、 C、 D、3. 英国曼彻斯特大学的两位科学家因为成功地从石墨中分离出石墨烯,荣获了诺贝尔物理学奖,石墨烯的理论厚度仅0.000 000 000 34米,将这个数用科学记数法表示为( )A、0.34×10-9 B、3.4×10-9 C、3.4×10-10 D、3.4×10-114. 以下说法正确的是( )A、在367人中至少有两个人的生日相同 B、一次摸奖活动的中奖率是1%,那么摸100次必然会中一次奖 C、一副扑克牌中,随意抽取一张是红桃K,这是必然事件 D、一个不透明的袋中装有3个红球,5个白球,搅匀从中任意摸出一个球,摸到红球的可能性大于摸到白球的可能性5. 如图,于点C,连接 , 若 , 则的度数为( ) A、 B、 C、 D、6. 如图,△ABC≌△DEC,点B,C,D在同一条直线上,且CE=2,CD=4,则BD的长为( )
A、 B、 C、 D、6. 如图,△ABC≌△DEC,点B,C,D在同一条直线上,且CE=2,CD=4,则BD的长为( )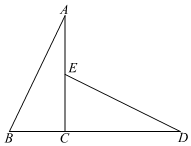 A、1.5 B、2 C、4.5 D、67. 一辆公共汽车从车站开出,加速行驶一段时间后开始匀速行驶.过了一段时间,汽车到达下一车站.乘客上下车后汽车开始加速,一段时间后又开始匀速行驶.下图中近似地刻画出汽车在这段时间内的速度变化情况的是( )A、
A、1.5 B、2 C、4.5 D、67. 一辆公共汽车从车站开出,加速行驶一段时间后开始匀速行驶.过了一段时间,汽车到达下一车站.乘客上下车后汽车开始加速,一段时间后又开始匀速行驶.下图中近似地刻画出汽车在这段时间内的速度变化情况的是( )A、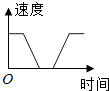 B、
B、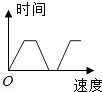 C、
C、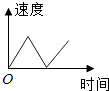 D、
D、 8. 已知等腰三角形的一边是5cm,另一边是6cm,这个三角形的周长为( )A、16cm B、17cm C、16cm或17cm D、以上都不对9. 若m+n=7,mn=12,则m2+n2的值是( )A、1 B、25 C、2 D、-10
8. 已知等腰三角形的一边是5cm,另一边是6cm,这个三角形的周长为( )A、16cm B、17cm C、16cm或17cm D、以上都不对9. 若m+n=7,mn=12,则m2+n2的值是( )A、1 B、25 C、2 D、-10二、填空题
-
10. 已知 , , 则.11. 已知和互为余角,和互为补角,且 , 则.12. 已知x2﹣y2=21,x﹣y=3,则x+y=.13. 如图,AD为∠BAC的平分线,请你添加一个适当的条件 , 使得 .
 14. 如图,中, , , 垂直平分交于 , 则.
14. 如图,中, , , 垂直平分交于 , 则. 15. 如图,把一张长方形纸片沿折叠后,点 , 分别落在 , 的位置,若 , 则的度数为.
15. 如图,把一张长方形纸片沿折叠后,点 , 分别落在 , 的位置,若 , 则的度数为.
三、解答题
-
16. 计算题:(1)、(2)、17. 先化简,再求值:[(xy﹣2)2+2xy﹣4]÷xy,其中x=10,y= .18. 小亮和小芳都想参加学校杜团组织的暑假实践活动,但只有一个名额,小亮提议用如下的办法决定谁去参加活动:将一个转盘9等分,分别标上1至9九个号码,随意转动转盘,若转到2的倍数,小亮去参加活动;转到3的倍数,小芳去参加活动;转到其它号码则重新转动转盘.
 (1)、转盘转到2的倍数的概率是多少?;(2)、你认为这个游戏公平吗?请说明理由.19. 小明某天上午时骑自行车离开家,时回到家,他有意描绘了离家的距离与时间的变化情况(如图所示).
(1)、转盘转到2的倍数的概率是多少?;(2)、你认为这个游戏公平吗?请说明理由.19. 小明某天上午时骑自行车离开家,时回到家,他有意描绘了离家的距离与时间的变化情况(如图所示). (1)、图象表示了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、时和时,他分别离家多远?(3)、他到达离家最远的地方是什么时间?离家多远?(4)、时到时他行驶了多少千米?(5)、他可能在哪段时间内休息,并吃午餐?(6)、他由离家最远的地方返回时的平均速度是多少?
(1)、图象表示了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、时和时,他分别离家多远?(3)、他到达离家最远的地方是什么时间?离家多远?(4)、时到时他行驶了多少千米?(5)、他可能在哪段时间内休息,并吃午餐?(6)、他由离家最远的地方返回时的平均速度是多少?