安徽省合肥市新站区2021-2022学年七年级下学期期末考试数学试题

试卷更新日期：2023-05-24 类型：期末考试

进入出卷网下载

一、单选题

1. ﹣ $\frac{1}{8}$ 的立方根是（　　）

A、﹣ $\frac{1}{2}$ B、 $\pm \frac{1}{2}$ C、 $\frac{1}{2}$ D、﹣ $\frac{1}{4}$

查看试题解析
2. 下列运算正确的是（）

A、 $(- m^{2}) \cdot m = m^{3}$ B、 $m^{2} + m^{3} = m^{5}$ C、 $m^{8} \div (m^{2})^{3} = m^{2}$ D、 $(m n)^{2} = m n^{2}$

查看试题解析
3. 若分式 $\frac{4}{x - 2}$ 有意义，则 $x$ 不能取的值是（）

A、 $0$ B、比 $0$ 小的数 C、 $2$ D、比 $2$ 小的数

查看试题解析
4. 世界最小生物，是澳大利亚昆士兰大学的科学家在外海由钻油平台从海底下约 $4.8$ 公里深处挖出的沙岩中发现的生物，它们的身长只有 $0.00000002 ～ 0.00000015$ 米，小于细胞，甚至比已知的最小细菌还要小，体积大概和病毒差不多．因此，这种生物刷新了地球生物最小体积的记录，其中 $0.00000015$ 用科学记数法表示为（）

A、 $1.5 \times 1 0^{7}$ B、 $15 \times 1 0^{- 6}$ C、 $0.15 \times 1 0^{- 8}$ D、 $1.5 \times 1 0^{- 7}$

查看试题解析
5. 计算 $(x + 1) (x - 2) - x^{2}$ 的结果是（）

A、 $- 2$ B、 $- x - 2$ C、 $x - 1$ D、 $x - 2$

查看试题解析
6. 代数式49m²-km+1是一个完全平方式，则k的值为（）

A、7 B、±7 C、14 D、±14

查看试题解析
7. 如图，已知直线 $m ∥ n$ ，某同学在这两条平行线之间画了一个直角三角形 $A C B$ ，如图所示，若 $∠ 1 = 25 °$ ，则 $∠ 3$ 的度数为（）

A、 $65 °$ B、 $55 °$ C、 $68 °$ D、 $70 °$

查看试题解析
8. 设 $m$ ， $n$ 是两个不为 $0$ 的实数，且满足 $m \leq - 2 n$ ，则下列结论正确的是（）

A、 $m < 0$ ， $n > 0$ B、 $n < m < 0$ C、 $\frac{m}{n} \leq - 2$ D、 $n + \frac{m}{2} \leq 0$

查看试题解析
9. 若关于 $x$ 的方程 $\frac{m x}{x + 3} = - \frac{3}{x + 3}$ 无解，则 $m$ 的值为（）

A、 $- 3$ B、 $0$ 或 $- 1$ C、 $0$ 或 $1$ D、 $- 3$ 或 $1$

查看试题解析
10. 如图，点A是直线m外一定点，点B，C是直线m上的两定点，点P是直线m上一动点，已知AB=6cm，BC=10cm，当动点P移动到点C处时，PA恰好垂直于AB，且此时PA=8cm，则当动点P在直线m上移动时，线段PA的最小值是（）

A、 $4.5 c m$ B、 $6 c m$ C、 $4.8 c m$ D、 $2.4 c m$

查看试题解析

二、填空题

11. 因式分解: $m^{2} n - 4 n =$ .

查看试题解析
12. 比较大小： $\frac{\sqrt{5} - 1}{2}$ $\frac{1}{2}$ ．

查看试题解析
13. 如图，已知 $A C ⊥ B C$ ， $C D ⊥ A B$ ， $D E ⊥ A C$ ， $F H ⊥ A B$ ，若 $∠ E D C = 55 °$ ；则 $∠ F H C =$ 度．

查看试题解析
14. 如图 $1$ 所示，将一张长为 $2 m$ ，宽为 $n (m > n)$ 的长方形纸片沿虚线剪成 $4$ 个直角三角形，拼成如图 $2$ 的正方形 $A B C D$ （相邻纸片之间不重叠，无缝隙），若正方形 $A B C D$ 的面积为 $20$ ，中间空白处的正方形 $E F G H$ 的面积为 $4$ ，则：

(1)、m+n；

(2)、原长方形纸片的周长是（用m表示）．

查看试题解析

三、解答题

15. 计算： $(- 2)^{2} + \sqrt{9} - (\frac{1}{3})^{- 1}$ ．

查看试题解析
16. 化简： $(2 x - \frac{1}{2} y) (2 x + \frac{1}{2} y) - (2 x - \frac{1}{2} y)^{2}$ ．

查看试题解析
17. 先化简，再求值： $(1 - \frac{1}{m - 1}) \cdot \frac{m^{2} - 1}{2 m - 4}$ ，其中 $m = 3$ ．

查看试题解析
18. 如图，在方格纸内将三角形 $A B C$ 经过平移后得到三角形 $A_{1} B_{1} C_{1}$ ，图中标出了点 $A$ 的对应点 $A_{1}$ ，解答下列问题．

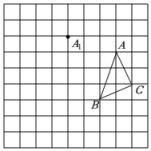(1)、在网格中画出三角形. $A_{1} B_{1} C_{1}$ .；

(2)、连接， $A A_{1}$ ， $B B_{1}$ ，则所得正方形. $A A_{1} B_{1} B$ .的面积是，它的边长 $A B$ 是．

查看试题解析
19. 已知 $2^{a} = 3$ ， $2^{b} = 9$ ， $2^{c} = 12$ ，求 $a + c - b$ 的值．

查看试题解析
20. 如图，是一幅平面镶嵌图案，它由相同的黑色正方形和白色等边三角形排列而成，观察图案，当正方形只有一个时，等边三角形有 $4$ 个（如图 $1$ ）；当正方形有 $2$ 个时，等边三角形有 $7$ 个（如图 $2$ ）；以此类推 $\dots$

(1)、若图案中每增加 $1$ 个正方形，则等边三角形增加个；

(2)、若图案中有 $n$ 个正方形，则等边三角形有个．

(3)、现有 $2022$ 个等边三角形，如按此规律镶嵌图案，要求等边三角形剩余最少，则需要正方形多少个？

查看试题解析
21. 2022年 $3$ 月上海爆发新一轮新冠疫情，全国疫情形式严峻，为此，合肥市开展了常态化免费核酸检测活动，有效地阻断了疫情的扩散，某生物公司受政府委托，活动当天需完成 $12$ 万份核算样本检测，为尽快出具核算检测结果，公司加派人手，检测效率比原计划提高了 $1.5$ 倍，结果提前 $2$ 小时完成任务，求该公司原计划每小时完成多少万份核酸样本检测？

查看试题解析
22. 继 $2008$ 年夏季奥运会之后， $2022$ 年北京又成功举办了冬季奥运会，使北京成为世界上首座“双奥之城”．本届冬奥会吉祥物“冰墩墩”和冬残奥会吉祥物“雪容融”的形象一经公布后，立即受到了人们的追捧．下表是市场在售的一款迷你型吉祥物的进价与售价：

进价

售价

冰墩墩

$10$ 元/件

$16$ 元/件

雪容融

$14$ 元/件

$18$ 元/件

暑假即将来临，七年级学生小王为了充实假期生活，计划用自己积攒的 $1168$ 元零花钱批发购进这两款吉祥物共 $100$ 件去夜市售卖，为此，在爸爸的帮助下，他进行了深入细致的市场调查，发现因为某些因素，当批发购进的冰墩墩不超过 $60$ 件时，两款吉祥物能全部售完；当批发购进的冰墩墩超过 $60$ 件时，超过 $60$ 件的冰墩墩需打 $5$ 折才能全部售完，雪容融都能正常售完．请帮小王算一算，在批发购进的 $100$ 件吉祥物全部售完的情况下，要使得利润不低于 $510$ 元，小王有几种进货方案？并指出利润最大的方案．

查看试题解析
23. 已知：直线 $A B ∥ C D$ ，经过直线 $A B$ 上的定点 $P$ 的直线 $E F$ 交 $C D$ 于点 $O$ ，点 $M$ ， $N$ 为直线 $C D$ 上的两点，且点 $M$ 在点 $O$ 右侧，点 $N$ 的左侧时，连接 $P M$ ， $P N$ ，满足 $∠ M P N = ∠ M N P$ ．

(1)、如图 $1$ ，若 $∠ M P O = 25 °$ ， $∠ M N P = 50 °$ ，直接写出 $∠ C O P$ 的度数为：．

(2)、如图 $2$ ，射线 $P Q$ 为 $∠ M P E$ 的角平分线，用等式表示 $∠ N P Q$ 与 $∠ P O M$ 之间的数量关系，并证明．

查看试题解析

	进价	售价
冰墩墩	$10$ 元/件	$16$ 元/件
雪容融	$14$ 元/件	$18$ 元/件