安徽省合肥市蜀山区2021-2022学年七年级下学期期末数学试题

试卷更新日期：2023-05-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个数中最小的实数是（）

A、0 B、 $- π$ C、 $- 2$ D、 $- 3$

查看试题解析
2. 据中新网报道，中国科学技术大学完成的“祖冲之二号”和“九章二号”量子计算优越性实验入选2021年国际物理学十大进展，人们发现全球目前最快的超级计算机用时2.3秒的计算量，“祖冲之二号”大约用时仅为0.00000022秒，将数字0.00000022用科学记数法表示为（）

A、 $2.2 \times 1 0^{- 8}$ B、 $2.2 \times 1 0^{- 6}$ C、 $2.2 \times 1 0^{- 7}$ D、 $22 \times 1 0^{- 8}$

查看试题解析
3. 下列算式中，结果等于 $a^{5}$ 的是（）

A、 $a^{2} + a^{3}$ B、 $a^{2} \cdot a^{3}$ C、 $(a^{2})^{3}$ D、 $a^{10} \div a^{2}$

查看试题解析
4. 如果把分式 $\frac{x - y}{2 x y}$ 中的 $x$ 和 $y$ 的值都扩大为原来2倍，则分式的值（）

A、缩小为原来的 $\frac{1}{2}$ B、扩大为原来的2倍 C、扩大为原来的4倍 D、不变

查看试题解析
5. 下列说法正确的是（）

A、无限小数都是无理数 B、两个无理数的和一定是无理数 C、分数可能是无理数 D、实数可以用数轴上的点来表示

查看试题解析
6. 将一副直角三角板按如图所示的方式叠放在一起，若 $A C ∥ D E$ ，则 $∠ B C E$ 的度数为（）

A、 $65 °$ B、 $70 °$ C、 $75 °$ D、 $80 °$

查看试题解析
7. 一元一次不等式组 ${\begin{array}{l} 3 x - 6 < x \\ x + 2 \geq 0 \end{array}$ 的解集中，最大的整数解是（）

A、2 B、3 C、 $- 2$ D、 $- 1$

查看试题解析
8. 如图，点 $E$ 在 $B C$ 上，下列条件中，不能判定 $A B ∥ D E$ 的是（）

A、 $∠ B = ∠ 5$ B、 $∠ 3 = ∠ 4$ C、 $∠ B + ∠ B E D = 180 °$ D、 $∠ 1 = ∠ 2$

查看试题解析
9. 如图，已知长方形 $A B C D$ 的面积为1，长与宽之差为1，则该长方形的周长为（）

A、2 B、 $\sqrt{5}$ C、 $2 \sqrt{5}$ D、 $\sqrt{3}$

查看试题解析
10. 如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“完美数”，如 $12 = 4^{2} - 2^{2}$ ， $52 = 1 4^{2} - 1 2^{2}$ ，因此12，52这两个数都是“完美数”，则下列结论中错误的是（）

A、20是“完美数” B、最小的“完美数”是4 C、“完美数”一定是4的奇数倍 D、小于30的所有“完美数”之和是60

查看试题解析

二、填空题

11. 若要使分式 $\frac{4 x}{x + 1}$ 有意义，则 $x$ 的取值范围是．

查看试题解析
12. 因式分解：am²－9a＝．

查看试题解析
13. 如图，点C在点B的北偏西 $60 °$ 的方向上，点C在点A的北偏西 $30 °$ 的方向上，则 $∠ C$ 等于度．

查看试题解析
14. 黄金比又称黄金律，是指事物各部分间一定的数学比例关系，即将整体一分为二，较大部分与较小部分之比等于整体与较大部分之比，其比值为 $\frac{\sqrt{5} + 1}{2}$ ，它介于整数 $n$ 和 $n + 1$ 之间，则 $n$ 的值是．

查看试题解析
15. 已知 $A B ∥ C D$ ， $∠ A B C = 50 °$ ，点 $M$ 在射线 $C B$ 上， $E$ 为线段 $C D$ 上一点，若 $∠ M E D = 100 °$ ，则 $∠ B M E =$ 度．

查看试题解析
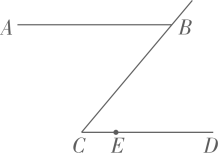16. 某高铁站客流量很大，某天开始售票时有 $n$ 个人在售票窗口等候购票，设购票人数按固定的速度增加，且每个窗口每分钟减少的排队人数也是固定的．若同时开放4个售票窗口，需要30分钟恰好不出现排队现象（即排队的人全部刚好购完票）；若同时开放6个售票窗口，需要10分钟恰好不出现排队现象，为减少旅客排队购票时间，车站承诺7分钟内不出现排队现象，则至少需要同时开放个售票窗口．

查看试题解析

三、解答题

17. 计算： $\sqrt[3]{- 64} + {(- \frac{1}{2})}^{- 2} - (π - 3.14)^{0}$ ．

查看试题解析
18. 解不等式： $\frac{2 + x}{3} - 1 \leq \frac{x}{2}$ ，并将其解集在数轴上表示出来．

查看试题解析
19. 如图，在每个小正方形的边长为1个单位的网格中， $△ A B C$ 的顶点均在格点（网格线的交点）上，按要求进行下列作图．

(1)、将 $△ A B C$ 先向右平移4个单位，再向上平移2个单位，请画出经两次平移后得到的 $△ A_{1} B_{1} C_{1}$ （其中点 $A$ 与点 $A_{1}$ 对应，点 $B$ 与点 $B_{1}$ 对应，点 $C$ 与点 $C_{1}$ 对应）；

(2)、连接 $A A_{1}$ 和 $C C_{1}$ ，则四边形 $A C C_{1} A_{1}$ 的面积为．

查看试题解析
20. 先化简，再求值： $(\frac{x^{2} - 4}{x^{2} - 4 x + 4} - \frac{1}{x - 2}) \div \frac{x + 1}{x + 2}$ ，其中 $x = \frac{1}{2}$ ．

查看试题解析
21. 观察个位上的数字是5的自然数的平方（任意一个个位数字为5的自然数可用代数式 $10 n + 5$ 来表示，其中 $n$ 为自然数），会发现一些有趣的规律．请你仔细观察，探索其规律，并归纳猜想出一般结论．
第1个等式： $1 5^{2} = (1 \times 2) \times 100 + 25$ ；

第2个等式： $2 5^{2} = (2 \times 3) \times 100 + 25$ ；

第3个等式： $3 5^{2} = (3 \times 4) \times 100 + 25$ ；

第4个等式： $4 5^{2} = (4 \times 5) \times 100 + 25$ ；

…

按照以上规律，解决下列问题：

(1)、写出第5个等式：；

(2)、写出你猜想的第 $n$ 个等式：（用含 $n$ 的等式表示）；

(3)、根据以上规律请计算 $202 5^{2}$ 的值，并写出计算过程．

查看试题解析
22. 如图，已知 $A C ∥ F E$ ， $∠ 1 + ∠ 2 = 180 °$ ．

(1)、请判断 $∠ F A B$ 与 $∠ C D B$ 是否相等，并说明理由；

(2)、若 $A C$ 平分 $∠ F A D$ ， $E F ⊥ B E$ 于点 $E$ ， $∠ F A D = 82 °$ ，求 $∠ B C D$ 的度数．

查看试题解析
23. 2022年2月20日，北京冬奥会顺利闭幕，冬奥会带来了冰雪消费热．某商场决定购进“冰墩墩”和“雪容融”两种纪念品进行销售，已知每件“冰墩墩”比每件“雪容融”的进价高20元，用2000元购进“冰墩墩”的数量和用1500元购进“雪容融”的数量相同．

(1)、求“冰墩墩”和“雪容融”每件的进价分别为多少元？

(2)、若每件“冰墩墩”的售价为100元，每件“雪容融"的售价为75元，商场决定用不超过14500元同时购进两种纪念品200件，并全部售完，若设“冰墩墩”进货 $a$ 件，请用含 $a$ 的代数式表示总利润，并说明该商场如何进货才能获得最大利润，求出最大利润．

查看试题解析