安徽省滁州市全椒县2021-2022学年七年级下学期期末数学试题

试卷更新日期：2023-05-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数是无理数的是（）

A、 $3.14$ B、 $\sqrt{9}$ C、 $\sqrt{3}$ D、 $\frac{22}{7}$

查看试题解析
2. 细菌的个体十分微小，大约10亿个细菌堆积起来才有一颗小米粒那么大，某种细菌的直径是0.0000025米，用科学记数法表示这种细菌的直径是（）

A、 $25 \times 1 0^{- 5}$ 米 B、 $2.5 \times 1 0^{- 7}$ 米 C、 $2.5 \times 1 0^{- 5}$ 米 D、 $2.5 \times 1 0^{- 6}$ 米

查看试题解析
3. 下列运算正确的是（）

A、 ${(- 3 a^{2})}^{3} = - 9 a^{6}$ B、 ${(- a)}^{2} \cdot a^{3} = a^{5}$ C、 ${(2 x - y)}^{2} = 4 x^{2} - y^{2}$ D、 $a^{2} + 4 a^{2} = 5 a^{4}$

查看试题解析
4. 如图，平移△ABC得到△DEF ，其中点A的对应点是点D ，则下列结论中不成立的是（）

A、AD∥BE B、∠BAC＝∠DFE C、AC＝DF D、∠ABC＝∠DEF

查看试题解析
5. 若k为正整数，则 ${(\underset{k 个 k}{\underset{︸}{k + k + \cdot \cdot \cdot + k}})}^{k} =$ （）

A、 $k^{2 k}$ B、 $k^{2 k + 1}$ C、 $2 k^{k}$ D、 $k^{2 + k}$

查看试题解析
6. 已知 $4 3^{2} = 1849 ， 4 4^{2} = 1936 ， 4 5^{2} = 2025 ， 4 6^{2} = 2116$ ，若n为整数，且 $n < \sqrt{2022} < n + 1$ ，则n的值为（）

A、42 B、43 C、44 D、45

查看试题解析
7. 定义新运算“ $\otimes$ ”，规定： $a \otimes b = a - 2 b$ ．若关于x的不等式 $x \otimes m > 3$ 的解集为 $x > - 1$ ，则m的值是（　　）

A、 $- 1$ B、 $- 2$ C、1 D、2

查看试题解析
8. 我国古代著作《四元玉鉴》记载“买椽多少”问题：“六贯二百一十钱，倩人去买几株椽．每株脚钱三文足，无钱准与一株椽．“其大意为：现请人代买一批椽，这批椽的价钱为6210文．如果每件椽的运费是3文，那么少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，试问6210文能买多少株椽？设这批椽的数量为 $x$ 株，则符合题意的方程是（）

A、 $3 (x - 1) = \frac{6210}{x}$ B、 $\frac{6210}{x - 1} = 3$ C、 $3 x - 1 = \frac{6210}{x}$ D、 $\frac{6210}{x} = 3$

查看试题解析
9. 如图，直线DE分别交射线BA，BG于点D，F，则下列条件中能判定DE $/ /$ BC的个数是（）
①∠ADE＝∠GBC；②∠DFB＝∠GBC；③∠EDB+∠ABC＝180°；④∠GFE＝∠GBC．

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 对于两个不相等的实数a，b，我们规定符号 $m i n {a ， b}$ 表示a，b中较小的值，如 $m i n {2 ， 4} = 2$ ．按照这个规定，方程 $m i n {\frac{1}{x} ， - \frac{1}{x}} = \frac{3}{x} - 1$ $(x \neq 0)$ 的解为（）

A、4 B、2 C、4或2 D、无解

查看试题解析

二、填空题

11. “x与y的2倍的和是正数”用不等式可以表示为．

查看试题解析
12. 因式分解： $7 a^{2} - 28 =$ ．

查看试题解析
13. 关于x的方程 $\frac{x}{x - 2} = 3 - \frac{m}{2 - x}$ 有增根，则m的值为

查看试题解析

三、解答题

14. 有长方形纸片，E，F分别是 $A D ， B C$ 上一点 $∠ D E F = x (0 ° < x < 45 °)$ ，将纸片沿 $E F$ 折叠成图1，再沿 $G F$ 折叠成图2．

(1)、如图1，当 $x = 32 °$ 时， $∠ F G D^{'} =$ 度；

(2)、如图2，作 $∠ M G F$ 的平分线 $G P$ 交直线 $E F$ 于点P，则 $∠ G P E =$ （用x的式子表示）．

查看试题解析
15. 计算： ${(- 2)}^{- 1} - \sqrt{\frac{1}{4}} + | \sqrt{3} - 2 | - {(\frac{1}{2})}^{0}$

查看试题解析
16. 计算：

(1)、 $(4 a^{2} b^{3} - 8 a^{3} b^{2}) \div (- 2 a b)^{2}$ ；

(2)、 $(2 x + y)^{2} + (x - y) (x + y) - 5 x (x - y)$ ．

查看试题解析
17. 解不等式组： ${\begin{array}{l} 2 (x - 2) \leq 2 - x ① \\ \frac{x + 1}{2} > \frac{x - 3}{3} + 1 ② \end{array}$ ，并把解集在数轴上表示出来．

查看试题解析
18. 先化简，再求值 $(\frac{3 a - 1}{a + 1} - a + 1) \div \frac{a^{2} - 6 a + 9}{a + 1}$ ，其中 $a = 2$ ．

查看试题解析
19. 如图，直线AB、CD交于点O，OM⊥AB，

(1)、若∠1=∠2，试判断ON与CD的位置关系，并说明理由.

(2)、若∠1= $\frac{1}{4}$ ∠BOC，试求∠MOD的度数.

查看试题解析
20. 观察以下等式：
第1个等式： $\frac{1}{1} - \frac{1}{1 \times 2} + \frac{1}{2} = 1$ ，

第2个等式： $\frac{1}{2} - \frac{1}{2 \times 3} + \frac{2}{3} = 1$ ，

第3个等式： $\frac{1}{3} - \frac{1}{3 \times 4} + \frac{3}{4} = 1$ ，

第4个等式： $\frac{1}{4} - \frac{1}{4 \times 5} + \frac{4}{5} = 1$ ，

……

按照以上规律，解决下列问题：

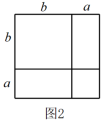
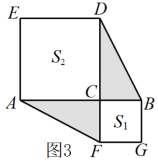
(1)、写出第5个等式：；

(2)、写出你猜想的第n（n为正整数）个等式：（用含n的等式表示），并证明.

查看试题解析
21. 数学课上，老师用图1中的一张边长为a的正方形纸片A，1张边长为b的正方形纸片B和2张宽与长分别为a与b的长方形纸片C，拼成了如图2所示的大正方形，观察图形并解答下列问题：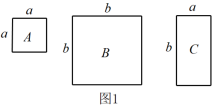

(1)、由图1和图2可以得到的等式为（用含a，b的等式表示）；

(2)、莉莉想用这三种纸片拼出一个面积为 $(2 a + b) (a + 2 b)$ 的大长方形，求需A，B，C三种纸片各多少张；

(3)、如图3，S₁ ， S₂分别表示边长为p，q的正方形的面积，且A，B，C三点在一条直线上， $S_{1} + S_{2} = 20$ ， $p + q = 6$ ．求图中阴影部分的面积．

查看试题解析
22. 为落实“美丽城区”的工作部署，市政府计划对城区道路进行改造，现安排甲、乙两个工程队完成．已知甲队的工作效率是乙队工作效率的 $\frac{3}{2}$ 倍，甲队改造480米的道路比乙队改造同样长的道路少用4天．

(1)、甲、乙两工程队每天能改造道路的长度分别是多少米？

(2)、若甲队工作一天需付费用3万元，乙队工作一天需付费用2.4万元，如需改造的道路全长1200米，改造总费用不超过66万元，至少安排甲队工作多少天？

查看试题解析
23. 知直线 $a / / b$ ，一块直角三角板的顶点A在直线a上，B，C两点在平面上移动，其中 $∠ A C B = 90 °$ ， $∠ B A C = 30 °$ ．请解答下列问题：

(1)、如图1，若点C在直线b上，点B在直线b的下方， $∠ 2 = 40 °$ ，求 $∠ 1$ 的度数：

(2)、如图2，若三角板的位置绕着点A进行转动，使得点C在直线a，b之间，点B在直线b的下方．
①请说明 $∠ α$ 和 $∠ β$ 的数量关系；
②若图中两个角的度数 $x °$ 和 $y °$ 之间满足关系式 $x^{2} - y^{2} = 12000$ ，求x，y的值．

查看试题解析