安徽省滁州市定远县池河片2021-2022学年七年级下学期期末考试数学试题

试卷更新日期：2023-05-24 类型：期末考试

进入出卷网下载

一、单选题

1. 9的平方根是（）

A、 3 B、±3 C、-3 D、 $\pm \sqrt{3}$

查看试题解析
2. 估计 $\sqrt{19} - 2$ 的值在（）

A、0到1之间 B、1到2之间 C、2到3之间 D、3到4之间

查看试题解析
3. 若 $a > b$ ，则下列各式中一定成立的是（）

A、 $a - 2 < b - 2$ B、 $a c^{2} > b c^{2}$ C、 $- 2 a > - 2 b$ D、 $a + 2 > b + 2$

查看试题解析
4. 把“a的3倍与2的和不小于6”用不等式表示得（）

A、 $3 a + 2 \geq 6$ B、 $3 a + 2 \leq 6$ C、 $3 a + 2 > 6$ D、 $3 a + 2 < 6$

查看试题解析
5. 我们定义一个新运算： $a & b = 1 0^{a} \times 1 0^{b}$ ，如 $2 & 3 = 1 0^{2} \times 1 0^{3} = 1 0^{5}$ ，那么 $4 & 8$ 为（）

A、 $1 0^{12}$ B、 $1 0^{32}$ C、 $1 2^{10}$ D、32

查看试题解析
6. 若 $a + b = 2$ ，则 $a^{2} - b^{2} + 4 b$ 的值是（）

A、0 B、2 C、4 D、6

查看试题解析
7. 当式子 $\frac{| x | - 3}{x^{2} - 2 x - 3}$ 的值为零时， $x$ 等于（）

A、4 B、-3 C、-1或3 D、3或-3

查看试题解析
8. 某煤厂原计划x天生产120吨煤，由于采用新的技术，每天增加生产3吨，因此提前2天完成任务，列出方程为（）

A、 $\frac{120}{x - 2} = \frac{120}{x} - 3$ B、 $\frac{120}{x} = \frac{120}{x + 2} - 3$ C、 $\frac{120}{x + 2} = \frac{120}{x} - 3$ D、 $\frac{120}{x} = \frac{120}{x - 2} - 3$

查看试题解析
9. 如图，点E在 $B C$ 的延长线上，下列条件不能判断 $A B ∥ C D$ 的是（）

A、∠5＝∠B B、 $∠ 1 = ∠ 2$ C、 $∠ B + ∠ B C D = 180 °$ D、 $∠ 3 = ∠ 4$

查看试题解析
10. 如图，直线a∥b，AC⊥AB，AC交直线b于点C，∠1＝60°，则∠2的度数是（）

A、30° B、35° C、45° D、50°

查看试题解析

二、填空题

11. 在实数 $\sqrt{5}$ ， $\frac{7}{22}$ ， $\sqrt[3]{- 8}$ ， $0$ ， $- 1.414$ ， $\frac{π}{2}$ ， $\sqrt{36}$ ， $0.101001000100001$ 中，无理数有个．

查看试题解析
12. 已知 $a^{m} = 2 ， a^{n} = 3$ ，则 $a^{m + 2 n} =$ .

查看试题解析
13. 已知关于x的分式方程 $\frac{x}{x - 1} - 2 = \frac{k}{1 - x}$ 的解为正数，则 $k$ 的取值范围为．

查看试题解析
14. 如图，直线 $A B$ ､ $C D$ 相交于点O， $O A$ 平分 $∠ C O E$ ，若 $∠ D O E = 106 °$ ，则 $∠ B O D =$

查看试题解析

三、解答题

15. 计算：

(1)、 $- 1^{2022} + {(- \frac{3}{2})}^{- 1} - \sqrt[3]{- 8} + (3.14 - π)^{0}$ ；

(2)、 $[x (x^{2} y^{2} - x y) - y (x^{2} - x^{3} y)] \div x^{2} y$ ．

查看试题解析
16. 先化简 $(\frac{a^{2} - 2 a + 1}{a^{2} - a} + \frac{a^{2} - 4}{a^{2} + 2 a}) \div \frac{2 a - 3}{a + 1}$ ；然后再从 $- 3$ ， $- 2$ ， $- 1$ ，0，1选择一个合适的数作为a的值，代入后再求值．

查看试题解析
17. 已知不等式组 ${\begin{array}{l} 3 (2 x - 1) < 2 x + 8 ① \\ 2 + \frac{3 (x + 1)}{8} > 3 - \frac{x - 1}{4} ② \end{array}$ ．

(1)、求此不等式组的解集，并写出它的整数解；

(2)、若上述整数解满足不等式 $a x + 6 \leq x - 2 a$ ，化简 $| a + 1 | - | a - 1 |$ ．

查看试题解析
18. 阅读材料：如果x是一个有理数，我们把不超过x的最大整数记作 $[x]$ ．
例如， $[3.2] = 3$ ， $[5] = 5$ ， $[- 2.1] = - 3$ ，那么， $x = [x] + a$ ，其中 $0 \leq a < 1$ ．

例如， $3.2 = [3.2] + 0.2$ ， $5 = [5] + 0$ ， $- 2.1 = [- 2.1] + 0.9$ ．

请你解决下列问题：

(1)、 $[4.8] =$ ， $[- 6.5] =$ ；

(2)、如果 $[x] = 5$ ，那么x的取值范围是；

(3)、如果 $[5 x - 2] = 3 x + 1$ ，那么x的值是；

(4)、如果 $x = [x] + a$ ，其中 $0 \leq a < 1$ ，且 $4 a = [x] + 1$ ，求x的值．

查看试题解析
19.

(1)、通过计算下列各式的值探究问题：
① $\sqrt{4^{2}}$ ＝  ▲  ； $\sqrt{1 6^{2}}$ ＝  ▲  ； $\sqrt{0^{2}}$ ＝  ▲  ； $\sqrt{(\frac{1}{9})^{2}}$ ＝  ▲   ．
探究：对于任意非负有理数a， $\sqrt{a^{2}}$ ＝  ▲   ．
② $\sqrt{(- 3)^{2}}$ ＝  ▲  ； $\sqrt{(- 5)^{2}}$ ＝  ▲  ； $\sqrt{(- 1)^{2}}$ ＝  ▲  ； $\sqrt{(- 2)^{2}}$ ＝  ▲   ．
探究：对于任意负有理数a， $\sqrt{a^{2}}$ ＝  ▲   ．
综上，对于任意有理数a， $\sqrt{a^{2}}$ ＝  ▲   ．

(2)、应用（1）所得的结论解决问题：有理数a，b在数轴上对应的点的位置如图所示，化简： $\sqrt{a^{2}}$ － $\sqrt{b^{2}}$ － $\sqrt{(a - b)^{2}}$ ＋|a＋b|.

查看试题解析
20. 2020年4月，随着蔚来中国总部落户合肥，全国新能源汽车之都已成为合肥新的代名词．某汽车经销商销售A，B两种型号的新能源汽车，已知购进3台A型新能源汽车和2台B型新能源汽车需要85万元，购进2台A型新能源汽车和1台B型新能源汽车需要50万元．

(1)、问A型，B型新能源汽车的单价分别是多少万元？

(2)、若该经销商计划购进A型和B型两种新能源汽车共20辆，费用不超过365万元，且A型新能源汽车的数量少于B型新能源汽车的数量，请你给出费用最省的方案，并求出该方案所需费用．

查看试题解析
21.

(1)、将一个多项式分组后，可提公因式或运用公式继续分解的方法是分组分解法．例如： $a m + a n + b m + b n = (a m + a n) + (b m + b n) = a (m + n) + b (m + n) = (a + b) (m + n)$ ．
①分解因式： $a b - a - b + 1$ ；
②若 $a ， b$ $(a > b)$ 都是正整数且满足 $a b - a - b - 4 = 0$ ，求 $a + b$ 的值；

(2)、若 $a ， b$ 为实数且满足 $a b - a - b - 4 = 0$ ， $s = a^{2} + 3 a b + b^{2} + 3 a - \frac{5}{2} b$ ，求 $s$ 的最小值．

查看试题解析
22. 填空完成下列推理过程
已知：如图，BD⊥AC，EF⊥AC，点D、F分别是垂足，∠1＝∠4．

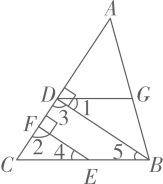
试说明：∠ADG＝∠C

解：∵BD⊥AC，EF⊥AC（已知）

∴∠2＝90°∠3＝90°（垂直的定义）

∴∠2＝∠3（等量代换）

∴BD∥EF

∴∠4＝∠5（两直线平行同位角相等）

∵∠1＝∠4（已知）

∠1＝∠5

∴DG∥CB（内错角相等两直线平行）

∴∠ADG＝∠C

查看试题解析
23. 已知：直线EF分别与直线AB，CD相交于点G，H，并且∠AGE+∠DHE＝180°．

(1)、如图1，求证：AB∥CD；

(2)、如图2，点M在直线AB，CD之间，连接GM，HM，求证：∠M＝∠AGM+∠CHM；

(3)、如图3，在（2）的条件下，射线GH是∠BGM的平分线，在MH的延长线上取点N，连接GN，若∠N＝∠AGM，∠M＝∠N+ $\frac{1}{2}$ ∠FGN，求∠MHG的度数．

查看试题解析