安徽省安庆市怀宁县2021-2022学年七年级下学期期末测试数学试卷

试卷更新日期：2023-05-24 类型：期末考试

进入出卷网下载

一、单选题

1. $\sqrt{16}$ 的算术平方根是（）

A、2 B、4 C、±2 D、±4

查看试题解析
2. 有下列实数： $\frac{π}{2}$ ， -3.14159， $\sqrt{8}$ ， 0， $\sqrt[3]{27}$ ， $\frac{22}{7}$ ， $0 . \overset{•}{3} \overset{•}{1}$ （31循环）其中无理数的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 据科技部生物中心消息，中国科学技术大学的研究团队开发了微米分辨率的肿瘤组织磁成像技术，相关成果已于2022年2月在《PNAS》发表．已知1微米＝0.000001米，数据“0.000001”用科学记数法表示为（）

A、 $1 \times 1 0^{- 5}$ B、 $0.1 \times 1 0^{- 6}$ C、 $1 \times 1 0^{- 6}$ D、 $0.1 \times 1 0^{- 5}$

查看试题解析
4. 下列运算正确的是（）

A、 $x^{2} \div x^{4} = \frac{1}{x^{2}}$ B、（x-y）²＝x²-y² C、 $\sqrt{(- 3)^{2}} = - 3$ D、（2x²）³＝6x⁶

查看试题解析
5. 实数2 $\sqrt{10}$ 介于（）

A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间

查看试题解析
6. 将一把直尺和一块含30°和60°角的三角板ABC按如图所示的位置放置，如果∠CDE=40°，那么∠BAF的大小为（）

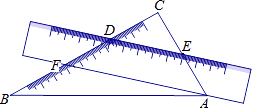A、10° B、15° C、20° D、25°

查看试题解析
7. 如果关于x的不等式（a+2）x＞a+2的解集为x＜1，那么a的取值范围是（　　）

A、a＞0 B、a＜0 C、a＞﹣2 D、a＜﹣2

查看试题解析
8. 将ΔABC沿BC方向平移3个单位得ΔDEF，若ΔDEF的周长等于8，则四边形ABFD的周长为（）

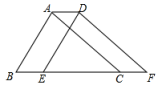A、14 B、12 C、10 D、8

查看试题解析
9. 怀远县政府在创建文明城市的进程中，着力美化城市环境，改造绿化涡河北岸，建设绿地公园，计划种植树木30万棵，由于青年志愿者的加入，实际每天植树比原计划多20%，结果提前5天完成任务，设原计划每天植树x万棵，可列方程为（）

A、 $\frac{30}{x} - \frac{30}{20 % x} = 5$ B、 $\frac{30}{20 % x} - \frac{30}{x} = 5$ C、 $\frac{30}{(1 + 20 %) x} - \frac{30}{x} = 5$ D、 $\frac{30}{x} - \frac{30}{(1 + 20 %) x} = 5$

查看试题解析
10. 边长分别为 $a$ 、 $b$ 且 $a = b + 1$ 的大小两个正方形如图所示摆放在一起，其中有一部分重叠，则阴影部分 $A$ 与阴影部分 $B$ 的面积差是（）

A、 $2 b + 1$ B、 $a b$ C、 $2 a + 1$ D、 $1$

查看试题解析

二、填空题

11. 分解因式：2a³﹣8a= ．

查看试题解析
12. 已知x+y＝8，xy＝14，则x²+y²＝．

查看试题解析
13. 分式方程 $\frac{x}{x - 3} + \frac{a}{x - 3} = 2$ 有增根，则a的值是．

查看试题解析
14. 若关于 x 的一元一次不等式组 ${\begin{array}{l} x - 2 m < 0 \\ x + m > 2 \end{array}$ 无解，则 m 的取值范围为．

查看试题解析
15. 点 $O$ 在直线 $A B$ 上， $O F ⊥ O C$ ， $∠ B O C ： ∠ B O D = 1 ： 3$ ， $∠ A O F = 2 ∠ C O D$ ，则∠ $A O C$ =

查看试题解析

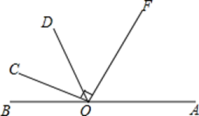
三、解答题

16. 计算： $- 1^{2022} - \sqrt[3]{27} \times (- \frac{1}{2})^{- 2} + (π - \sqrt{2})^{0} - | - 4 | + \sqrt{9}$ ．

查看试题解析
17. 解不等式组： ${\begin{array}{l} \frac{5 x + 1}{2} - \frac{2 x - 1}{3} \geq - 1 \\ (x - 3)^{2} - (x + 2) (x - 2) > 1 \end{array}$ ，并写出不等式组的整数解．

查看试题解析
18. 先化简，再求值： $(\frac{a^{2} - 2 a}{a^{2} - 4 a + 4} - \frac{3}{a - 2}) \div \frac{a - 3}{a^{2} - 4}$ ，从-2，0，2，3中选取一个你认为合适的数作为a的值．

查看试题解析
19. 如图，在正方形网格中有一个格点三角形ABC（即ΔABC的各顶点都在格点上），按要求进行下列作图：

(1)、画出点C到线段AB的垂线段，垂足为D；

(2)、画出将ΔABC先向左平移2格，再向上平移3格后的ΔA^/B^/C^/；

(3)、画一条直线m，将ΔABC分成两个面积相等的三角形．

查看试题解析
20. 先阅读下面的解题过程，再解答问题：
如图①，已知AB $∥$ CD，∠B＝40°，∠D＝30°，求∠BED的度数．

解：过点E作EF $∥$ AB，则AB $∥$ CD $∥$ EF．

因为EF $∥$ AB，所以∠1＝∠B＝40°

又因为CD $∥$ EF，所以∠2＝∠D＝30°

所以∠BED＝∠1+∠2＝40°+30°＝70°．

如图②是小军设计的智力拼图玩具的一部分，现在小军遇到两个问题，请你帮他解决：

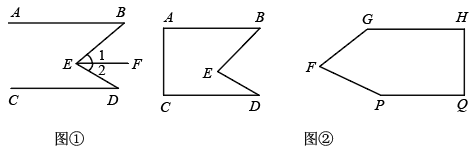(1)、如图②∠B＝45°，∠BED＝75°，为了保证AB $∥$ CD，∠D必须是多少度？请写出理由．

(2)、如图②，当∠G、∠GFP、∠P满足什么关系时，GH $∥$ PQ，请写出满足关系的式子，并说明理由．

查看试题解析
21. 某社区去年购买了A、B两种型号的共享单车，购买A种单车共花费15000元，购买B种单车共花费14000元，购买A种单车的数量是购买B种单车数量的1.5倍，且购买一辆A种单车比购买一辆B种单车少200元．

(1)、求去年购买一辆A种和一辆B种单车各需要多少元？

(2)、为积极响应政府提出的“绿色发展•低碳出行”号召，该社区决定今年再买A、B两种型号的单车共60辆，恰逢厂家对A、B两种型号单车的售价进行调整，A种单车售价比去年购买时提高了10%，B种单车售价比去年购买时降低了10%，如果今年购买A、B两种单车的总费用不超过34000元，那么该社区今年最多购买多少辆B种单车？

查看试题解析
22. 如图，已知AM $∥$ BN，∠A=60°，点P是射线AM上一动点 $($ 与点A不重合 $)$ ， BC、BD分别平分∠ABP和∠PBN，分别交射线AM于点C，D．

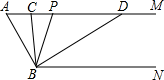(1)、求∠CBD的度数；

(2)、当点P运动时，∠APB与∠ADB之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由；若变化，请写出变化规律．

(3)、当点P运动到使∠ACB=∠ABD时，直接写出∠ABC的度数是．

查看试题解析