广东省深圳市龙华区2022-2023学年下学期九年级调研测试数学试卷
试卷更新日期:2023-05-24 类型:月考试卷
一、选择题(本大题共10小题,每小题3分,共30分。)
-
1. 砚台与笔、墨、纸是中国传统的文房四宝,是中国书法的必备用具.下图是一方寓意“规矩方圆”的砚台,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 在《九章算术》一书中,对开方开不尽的数起了一个名字,叫做“面”.这是中国传统数学对无理数的最早记载.下面符合“面”的描述的数是( )A、 B、 C、 D、3. 下列运算正确的是( )A、x2+x2=x4 B、y3·y2=y6 C、(x+y)(x-y)=x2-y2 D、(x+y)2=x2+y24. 农户利用“立体大棚种植技术”把毛豆和芹菜进行混种.已知毛豆齐苗后棚温在18~25℃最适宜,播种芹菜的最适宜温度是15~20℃.农户在毛豆齐苗后在同一大棚播种了芹菜,这时应该把大棚温度设置在下列哪个范围最适宜( )A、15~18℃ B、18~20℃ C、20~25℃ D、20℃以上5. 如图,某商场有一自动扶梯,其倾斜角为α,高为h米,扶梯的长度是( )
2. 在《九章算术》一书中,对开方开不尽的数起了一个名字,叫做“面”.这是中国传统数学对无理数的最早记载.下面符合“面”的描述的数是( )A、 B、 C、 D、3. 下列运算正确的是( )A、x2+x2=x4 B、y3·y2=y6 C、(x+y)(x-y)=x2-y2 D、(x+y)2=x2+y24. 农户利用“立体大棚种植技术”把毛豆和芹菜进行混种.已知毛豆齐苗后棚温在18~25℃最适宜,播种芹菜的最适宜温度是15~20℃.农户在毛豆齐苗后在同一大棚播种了芹菜,这时应该把大棚温度设置在下列哪个范围最适宜( )A、15~18℃ B、18~20℃ C、20~25℃ D、20℃以上5. 如图,某商场有一自动扶梯,其倾斜角为α,高为h米,扶梯的长度是( )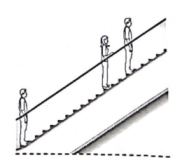 A、 B、hcosα C、hsinα D、6. 下图是小杰同学家中的一个30min沙漏计时器, 相关实验结果表明,沙漏中的沙下落的速度可以近似看成匀速,从计时器开始计时到计时30min止,上面玻璃球内的含沙量Q(cm3)与时间t(min)之间的函数关系图象大致为( )
A、 B、hcosα C、hsinα D、6. 下图是小杰同学家中的一个30min沙漏计时器, 相关实验结果表明,沙漏中的沙下落的速度可以近似看成匀速,从计时器开始计时到计时30min止,上面玻璃球内的含沙量Q(cm3)与时间t(min)之间的函数关系图象大致为( ) A、
A、 B、
B、 C、
C、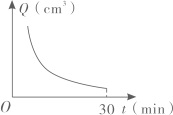 D、
D、 7. 如图,这条活灵活现的“小鱼”是由若干条线段组成的,它是一个轴对称图形,对称轴为直线I,则下列结论不一定正确的是( )
7. 如图,这条活灵活现的“小鱼”是由若干条线段组成的,它是一个轴对称图形,对称轴为直线I,则下列结论不一定正确的是( ) A、点C和点D到直线I的距离相等 B、BC=BD C、∠CAB=∠DAB D、四边形ADBC是菱形8. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,D,E分别是BC,AC的中点,连接DE.以点A为圆心,适当长度为半径作弧,分别交AC,AB于点M,N;以点D为圆心,AM长为半径作弧交DE于点P;以点P为圆心,MN长为半径作弧,交前面的弧于点Q;作射线DQ交AB于点F.则AF的长为( )
A、点C和点D到直线I的距离相等 B、BC=BD C、∠CAB=∠DAB D、四边形ADBC是菱形8. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,D,E分别是BC,AC的中点,连接DE.以点A为圆心,适当长度为半径作弧,分别交AC,AB于点M,N;以点D为圆心,AM长为半径作弧交DE于点P;以点P为圆心,MN长为半径作弧,交前面的弧于点Q;作射线DQ交AB于点F.则AF的长为( ) A、3 B、4 C、5 D、69. 某公司去年10月份的营业额为2500万元,后来公司改变营销策略,12月份的营业额达到3780万元,已知12月份的增长率是11月份的1.3倍,求11月份的增长率。设11月份的增长率为x,根据题意,可列方程为( )A、2500(1+x)(1+1.3x)=3780 B、2500(1+x)2=3780 C、2500(1+1.3x)2=3780 D、2500(1+2.3x)=378010. 如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,连接CD,若∠ACD=2∠B, , 则的值是( )
A、3 B、4 C、5 D、69. 某公司去年10月份的营业额为2500万元,后来公司改变营销策略,12月份的营业额达到3780万元,已知12月份的增长率是11月份的1.3倍,求11月份的增长率。设11月份的增长率为x,根据题意,可列方程为( )A、2500(1+x)(1+1.3x)=3780 B、2500(1+x)2=3780 C、2500(1+1.3x)2=3780 D、2500(1+2.3x)=378010. 如图,在Rt△ABC中,∠ACB=90°,D是AB上一点,连接CD,若∠ACD=2∠B, , 则的值是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共5小题,每小题3分,共15分)
-
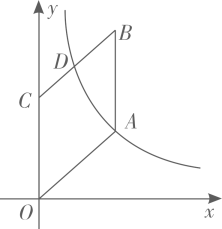
11. 计算:|-5|+tan45°=12. 新学期开始,小颖从学校开设的感兴趣的5门劳动教育课程:烹饪、茶艺、花卉种植、整理收纳、家电维修中,随机选择-一门课程学习,她选择“茶艺”课程的概率是 .13. 已知是方程组的解,则m+n= .14. 如图,在平面直角坐标系中,OA=3,将OA沿y轴向上平移3个单位至CB,连接AB,若反比例函数y=(x>0)的图象恰好过点A与BC的中点D,则k= .
 15. 如图,在边长为4米的正方形场地ABCD内,有一块以BC为直径的半圆形红外线接收“感应区”,边AB上的P处有一个红外线发射器,红外线从点P发射后,经AD、CD.上某处的平面镜反射后到达“感应区”.若AP=1米,当红外线途经的路线最短时,AD上平面镜的反射点距离点A米.
15. 如图,在边长为4米的正方形场地ABCD内,有一块以BC为直径的半圆形红外线接收“感应区”,边AB上的P处有一个红外线发射器,红外线从点P发射后,经AD、CD.上某处的平面镜反射后到达“感应区”.若AP=1米,当红外线途经的路线最短时,AD上平面镜的反射点距离点A米.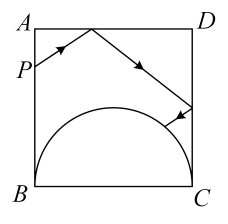
三、解答题(本大题共7小题,共55分)
-
16. 解不等式组17. 先化简、再求值: , 其中x=2.18. 为了解九年级学生对某个知识点的掌握程度,某校对九年级学生以20人一组进行了随机分组,开展了一次素养调研,并用SOLO评分模型进行评分:“完全不理解”记为0分,“了解了一个方面”记为1分,“了解了几个独立的方面”记为2分,“理解了 几个方面的相关性”记为3分,“能够综合运用”记为4分,现从调查结果中随机抽取了3个小组学生的得分,进行统计分析,过程如下:
[整理与描述]
 (1)、请补全第1小组得分条形统计图:第2小组得分扇形统计图中,“得分为3 分”这一项所对应的圆心角的度数为°(2)、[分析与估计]
(1)、请补全第1小组得分条形统计图:第2小组得分扇形统计图中,“得分为3 分”这一项所对应的圆心角的度数为°(2)、[分析与估计]平均数
众数
中位数
第1组
2.9
a
3
第2组
b
0
1
第3组
2.25
2
c
由上表填空:a= , b= , c=;
(3)、若该校九年级有600名学生,请你估计该校九年级学生在调研中表现为“能够综合运用”的人数有人;(4)、 [评价与建议]结合你的分析,请给第2组的同学提供一条有关该知识点的学习建议.
19. 如图,⊙O是△ABC的外接圆,连接OA,过点C作一条射线CD. (1)、请从以下条件中:①CD∥AO,∠ABC=45°;②∠BCD=∠BAC;③CB平分∠ACD.选择一组能证明CD是⊙O的切线的条件,并写出证明过程;(2)、若OA=2,∠OAB=22.5°,AB=CB,求的长度.(结果保留π)20. 随着天气转暖,越来越多的市民喜欢到户外活动,小明与同学约定周末带帐篷到附近露营地开展活动.
(1)、请从以下条件中:①CD∥AO,∠ABC=45°;②∠BCD=∠BAC;③CB平分∠ACD.选择一组能证明CD是⊙O的切线的条件,并写出证明过程;(2)、若OA=2,∠OAB=22.5°,AB=CB,求的长度.(结果保留π)20. 随着天气转暖,越来越多的市民喜欢到户外活动,小明与同学约定周末带帐篷到附近露营地开展活动.
 (1)、[买帐篷]经了解,某种帐篷有A、B两种型号,已知A型帐篷的单价比B型帐篷的单价多30元,用1200元购买A型帐篷的数量和用900元购买B型帐篷的数量相同.小明买了A、B两种型号帐篷各2个,共需多少钱?(2)、[摆帐篷]周末,小明与同学一起来到露营地,发现有一块由篱笆围绕的长20米,宽14米的矩形草地(抽象成如图11的20×14的方格纸)可用来摆帐篷.经测量,每个帐篷占据的地面部分是半径为3米的圆形(抽象成如图10的圆),为保障通行,帐篷四周需要留有通道,通道最狭窄处的宽度不小于I米.小明将第一个帐篷按要求摆放在如图所示的位置,此块草地内最多还能摆下几个同样大小的帐篷呢?请在图11中画出符合要求的设计示意图.(要求:圆心要画在格点上,画圆时要用圆规)21. 如图:
(1)、[买帐篷]经了解,某种帐篷有A、B两种型号,已知A型帐篷的单价比B型帐篷的单价多30元,用1200元购买A型帐篷的数量和用900元购买B型帐篷的数量相同.小明买了A、B两种型号帐篷各2个,共需多少钱?(2)、[摆帐篷]周末,小明与同学一起来到露营地,发现有一块由篱笆围绕的长20米,宽14米的矩形草地(抽象成如图11的20×14的方格纸)可用来摆帐篷.经测量,每个帐篷占据的地面部分是半径为3米的圆形(抽象成如图10的圆),为保障通行,帐篷四周需要留有通道,通道最狭窄处的宽度不小于I米.小明将第一个帐篷按要求摆放在如图所示的位置,此块草地内最多还能摆下几个同样大小的帐篷呢?请在图11中画出符合要求的设计示意图.(要求:圆心要画在格点上,画圆时要用圆规)21. 如图: (1)、[课本再现]把两个全等的矩形ABCD和矩形CEFG拼成如图12的图案,则∠ACF= °(2)、[迁移应用]如图13,在正方形ABCD中,E是CD边上一点(不与点C,D重合),连接BE,将BE绕点E顺时针旋转90°至FE,作射线FD交BC的延长线于点G,求证:CG=BC;(3)、[拓展延伸]在菱形ABCD中,∠A=120°,E是CD边上一点(不与点C,D重合),连接BE,将BE绕点E顺时针旋转120°至FE,作射线FD交BC的延长线于点G.
(1)、[课本再现]把两个全等的矩形ABCD和矩形CEFG拼成如图12的图案,则∠ACF= °(2)、[迁移应用]如图13,在正方形ABCD中,E是CD边上一点(不与点C,D重合),连接BE,将BE绕点E顺时针旋转90°至FE,作射线FD交BC的延长线于点G,求证:CG=BC;(3)、[拓展延伸]在菱形ABCD中,∠A=120°,E是CD边上一点(不与点C,D重合),连接BE,将BE绕点E顺时针旋转120°至FE,作射线FD交BC的延长线于点G.①线段CG与BC的数量关系是;
②若AB=6,E是CD的三等分点,则△CEG的面积为。
22. [定义]若抛物线与一水平直线交于两点,我们把这两点间线段的长称为抛物线关于这条直线的跨径,抛物线的顶点到该直线的距离称为抛物线关于这条直线的矢高,矢高与跨径的比值称为抛物线关于这条直线的矢跨比.(1)、如图,抛物线y=ax2+bx+c的顶点为P,PC⊥x轴于点C,它与x轴交于点A,B,则AB的长为抛物线y=ax2+bx+c关于x轴的跨径,PC的长为抛物线y=a2+bx+c关于x轴的矢高,的值为抛物线y=ax2+bx+c关于x轴的矢跨比. (2)、[特例]如图15,已知抛物线y=-x2+4与x轴交于点C,D (点C在点D右侧):
(2)、[特例]如图15,已知抛物线y=-x2+4与x轴交于点C,D (点C在点D右侧):①抛物线y=-x2+4关于x轴的矢高是 , 跨径是 , 矢跨比是;
②有一抛物线经过点c,与抛物线y=-x2+4开口方向与大小一样,且矢高是抛物线y=-x2+4关于x轴的矢高的 , 求它关于x轴的矢跨比;
 (3)、[推广]结合抛物线的平移规律可以发现,两条开口方向与大小一样的抛物线,若第一条抛物线的矢高是第二条抛物线关于同一直线的矢高的k(k>0)倍,则第一条抛物线的跨径是第二条抛物线关于同一直线的跨径的倍(用含k的代数式表示);(4)、[应用]如图16是某地一座三拱桥梁建筑示意图,其中主跨与边跨的拱轴线为开口方向与大小一样的抛物线,它们关于水平钢梁所在直线的跨径分别为420米与280米,已知主跨的矢跨比为 , 则边跨的矢跨比是。
(3)、[推广]结合抛物线的平移规律可以发现,两条开口方向与大小一样的抛物线,若第一条抛物线的矢高是第二条抛物线关于同一直线的矢高的k(k>0)倍,则第一条抛物线的跨径是第二条抛物线关于同一直线的跨径的倍(用含k的代数式表示);(4)、[应用]如图16是某地一座三拱桥梁建筑示意图,其中主跨与边跨的拱轴线为开口方向与大小一样的抛物线,它们关于水平钢梁所在直线的跨径分别为420米与280米,已知主跨的矢跨比为 , 则边跨的矢跨比是。