人教版八年级下数学期末复习知识点扫盲满分计划——19.1变量与函数
试卷更新日期:2023-05-24 类型:复习试卷
一、函数的概念与解析式:有唯一确定的y与x对应
-
1. 下列图象中,表示y是x的函数的个数有( )
 A、1 B、2个 C、3个 D、4个2. 下列表达式中,y不是x的函数的是( )A、y=±6x B、y=6x2+x+1 C、y=6x+3 D、y=3. 下列图形中,不能表示是函数的是( )A、
A、1 B、2个 C、3个 D、4个2. 下列表达式中,y不是x的函数的是( )A、y=±6x B、y=6x2+x+1 C、y=6x+3 D、y=3. 下列图形中,不能表示是函数的是( )A、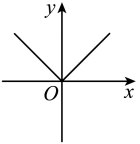 B、
B、 C、
C、 D、
D、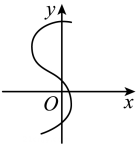 4. 下列曲线中,不表示是的函数图象的是( )A、
4. 下列曲线中,不表示是的函数图象的是( )A、 B、
B、 C、
C、 D、
D、 5. 下列所描述的四个变化过程中,变量之间的关系不能看成函数关系的是( )A、三角形的一个外角度数度和与它相邻的内角度数度的关系 B、树的高度为60厘米,每个月长高3厘米,月后树的高度为厘米,与的关系 C、正方形的面积(平方厘米)和它的边长(厘米)的关系 D、一个正数的平方根是 , 随着这个数的变化而变化,与之间的关系
5. 下列所描述的四个变化过程中,变量之间的关系不能看成函数关系的是( )A、三角形的一个外角度数度和与它相邻的内角度数度的关系 B、树的高度为60厘米,每个月长高3厘米,月后树的高度为厘米,与的关系 C、正方形的面积(平方厘米)和它的边长(厘米)的关系 D、一个正数的平方根是 , 随着这个数的变化而变化,与之间的关系二、函数自变量的取值范围:分母不为0,根号下不为负,0次幂底数不为0
-
6. 函数的自变量x的取值范围是( )A、x≠0 B、x≥且x≠0 C、x> D、x≥7. 函数自变量的取值范围是( )A、 B、 C、且 D、且8. 已知函数求x的取值范围 .9. 已知 , 则自变量 x 的取值范围为 .10. 函数的自变量x的取值范围是( )A、且 B、且 C、 D、且
三、函数自变量的值或函数的值
-
11. 变量与的关系式是 , 当自变量时,因变量的值是( )A、-5 B、5 C、1 D、-112. 函数中,自变量x的取值范围为 . 当时,此函数值为 .13. 当时,函数的值是 .14. 变量x与y之间的关系式是y=35x+20,当自变量x=2时,因变量y的值是( )A、90 B、65 C、70 D、7515. 已知一次函数 ,当 时,函数值y等于( ).A、0 B、1 C、6 D、7
四、用解析式表示函数
-
16. 一个底面是正方形的长方体,高为4cm,底面正方形边长为3cm.如果它的高不变,把底面正方形边长增加了xcm,则所得长方体增加的体积V(cm3)与x(cm)之间的关系式是 .17. 在一个边长为1的正方形中挖去一个边长为的小正方形,如果设剩余部分的面积为y,那么y关于x的函数表达式为( )A、 B、 C、 D、18. 某商店进了一批货,每件进价为4元,售价为每件6元,如果售出件,售出件的总利润为元,则与的函数关系式为.19. 如图,长为32米,宽为20米的长方形地面上,修筑宽度均为m米的两条互相垂直的小路(图中阴影部分),其余部分作耕地,如果将两条小路铺上地砖,选用地砖的价格是60元/米2 .
 (1)、写出买地砖需要的钱数y(元)与m(米)的函数关系式 .(2)、计算当m=3时,地砖的费用.20. 已知一个等腰三角形的腰长为x,底边长为y,周长是10,则底边y关于腰长x之间的函数关系式及定义域为( )A、y=10﹣2x(5<x<10) B、y=10﹣2x(2.5<x<5) C、y=10﹣2x(0<x<5) D、y=10﹣2x(0<x<10)
(1)、写出买地砖需要的钱数y(元)与m(米)的函数关系式 .(2)、计算当m=3时,地砖的费用.20. 已知一个等腰三角形的腰长为x,底边长为y,周长是10,则底边y关于腰长x之间的函数关系式及定义域为( )A、y=10﹣2x(5<x<10) B、y=10﹣2x(2.5<x<5) C、y=10﹣2x(0<x<5) D、y=10﹣2x(0<x<10)五、用图像表示函数的关系
-
21. 小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与离家距离的关系示意图.根据图中提供的信息回答下列问题:
 (1)、小明家到学校的路程是米.(2)、小明在书店停留了分钟.(3)、本次上学途中,小明一共行驶了米.一共用了分钟.(4)、在整个上学的途中哪个时间段小明骑车速度最快,最快的速度是多少米分?22. 对于函数 ,小明根据学习一次函数和反比例函数的经验,研究了它的图象和性质.下面是小明的分析和研究过程,请补充完整.
(1)、小明家到学校的路程是米.(2)、小明在书店停留了分钟.(3)、本次上学途中,小明一共行驶了米.一共用了分钟.(4)、在整个上学的途中哪个时间段小明骑车速度最快,最快的速度是多少米分?22. 对于函数 ,小明根据学习一次函数和反比例函数的经验,研究了它的图象和性质.下面是小明的分析和研究过程,请补充完整.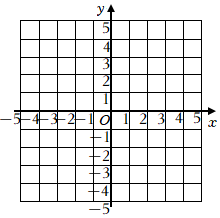 (1)、自变量 的取值范围是.
(1)、自变量 的取值范围是.-1
0
1
3
4
5
-2
-3
-6
6
3
2
(2)、根据列表计算的部分对应值,在平面直角坐标系中用描点法画出该函数的图象.(3)、从中心对称和轴对称的角度分析图象特征,并说说这个函数的增减性.23. 在学习函数的过程中,我们经历了通过列表,描点,连线来画函数图象,观察分析图象特征,从而概括出函数的性质的过程.下面是研究函数 性质及其应用的部分过程,请按要求完成下列各小题.列表:
…
-5
-4
-3
-2
-1
0
1
2
3
…
…
1
0
1
…
 (1)、请求出表中 , 的值,并在图中画出该函数的图象;(2)、根据函数图象,写出该函数的一条性质;(3)、若直线 与函数 的图象恰好有两个交点,请直接写出 的取值范围.24. 九年级某数学兴趣小组在学习了反比例函数的图象与性质后,进一步研究函数的图象与性质,探究过程如下:
(1)、请求出表中 , 的值,并在图中画出该函数的图象;(2)、根据函数图象,写出该函数的一条性质;(3)、若直线 与函数 的图象恰好有两个交点,请直接写出 的取值范围.24. 九年级某数学兴趣小组在学习了反比例函数的图象与性质后,进一步研究函数的图象与性质,探究过程如下: (1)、写出自变量x的取值范围;(2)、画函数图象;
(1)、写出自变量x的取值范围;(2)、画函数图象;列表:下表是x与y的几组对应值,其中 ▲ ;
x
…
-3
-2
-1
1
2
3
…
y
…
1
2
4
4
2
m
…
描点画图:利用所给的网格,建立平面直角坐标系,描出表中各对对应值为坐标的点,画出该函数图象;
(3)、通过观察图象,写出该函数的两条性质:①;
②.
25. 在函数的学习中,我们经历了“确定函数表达式、画函数图象、利用函数图象研究函数性质”的学习过程下表是一个函数的自变量与函数值的部分对应值,请你借鉴以往学习函数的经验,探究下列问题:0.5
1
2
3
4
5
6
2.5
2
2.5
3.3
4.3
5.2
6.2
 (1)、当时,.(2)、根据表中数值描点并画出函数图象;(3)、观察画出的函数图象,写出这个函数的一条性质
(1)、当时,.(2)、根据表中数值描点并画出函数图象;(3)、观察画出的函数图象,写出这个函数的一条性质六、综合训练
-
26. 如图,是一个“函数求值机”示意图,其中y是x的函数.下面表格中,是通过该“函数求值机”得到的几组x与y的对应值.

输入x
…
0
2
…
输出y
…
19
15
11
0
8
…
根据以上信息,解答下列问题:
(1)、当输入的x值为时,输出的y值为;(2)、求k2 , b的值;(3)、当输出的y值为24时,求输入的x值.27. 已知等腰三角形的周长为12,设腰长为x,底边长为y.(1)、试写出y关于x的函数表达式,并直接写出自变量x的取值范围.(2)、当x=5时,求出函数值.28. 根据如图所示的程序计算函数的值,若输入的值是2,则输出的值是1,若输入的值是7,则输出的值是( ) A、1 B、-1 C、2 D、-229. 父亲告诉张云:“距离地面越高,温度越低”,并给张云出示了下面的表格:
A、1 B、-1 C、2 D、-229. 父亲告诉张云:“距离地面越高,温度越低”,并给张云出示了下面的表格:距离地面高度(千米)
0
1
2
3
4
5
温度(℃)
20
14
8
2
-4
-10
根据上表,父亲还给张云出了下面几个问题,请你和张云一起回答.
(1)、上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、如果用h表示距离地面的高度,用t表示温度,那么随着的变化,是怎么变化的?(3)、你能猜出距离地面6千米的高空温度是多少吗?30. 深圳某中学的小明和朱老师一起到一条笔直的跑道上跑步,到达起点后小明做了一会儿准备活动,朱老师先跑.当小明出发时,朱老师已经距起点200 m了.他们距起点的距离s (m)与小明出发的时间1 (s)之间的关系如图所示(不完整) .据图中给出的信息,解答下列问题: (1)、在上述变化过程中,自变量是 , 因变量是(2)、小明出发时,朱老师的速度为m/s,小明的速度为m/s;(3)、当小明第一次追上朱老师时,求小明距起点的距离.31. 周末小刚骑自行车到外婆家,他从家出发后到达书店,看了一会书,仍按原来的速度继续前行到达外婆家,小刚从家出发到外婆家中,小刚与家的距离随时间变化的函数图象大致如图所示,下列说法正确的是( )
(1)、在上述变化过程中,自变量是 , 因变量是(2)、小明出发时,朱老师的速度为m/s,小明的速度为m/s;(3)、当小明第一次追上朱老师时,求小明距起点的距离.31. 周末小刚骑自行车到外婆家,他从家出发后到达书店,看了一会书,仍按原来的速度继续前行到达外婆家,小刚从家出发到外婆家中,小刚与家的距离随时间变化的函数图象大致如图所示,下列说法正确的是( ) A、小刚从家到书店的骑行速度为5km/h B、小刚在书店停留了1.5h C、书店与外婆家的距离为15km D、小刚从家到外婆家的平均速度为6km/h32. 函数y=的自变量x的取值范围是33. 一个圆形花坛,面积S与半径的函数关系式中关于常量和变量的表述正确的是( )A、常量是2,变量是、、 B、常量是2、 , 变量是、 C、常量是2,变量是、 D、常量是 , 变量是、34. 如图表示的是嘉淇父母外出散步时,离家的距离与时间的函数关系.(图代表嘉淇的母亲,图代表嘉淇的父亲)
A、小刚从家到书店的骑行速度为5km/h B、小刚在书店停留了1.5h C、书店与外婆家的距离为15km D、小刚从家到外婆家的平均速度为6km/h32. 函数y=的自变量x的取值范围是33. 一个圆形花坛,面积S与半径的函数关系式中关于常量和变量的表述正确的是( )A、常量是2,变量是、、 B、常量是2、 , 变量是、 C、常量是2,变量是、 D、常量是 , 变量是、34. 如图表示的是嘉淇父母外出散步时,离家的距离与时间的函数关系.(图代表嘉淇的母亲,图代表嘉淇的父亲)①嘉淇的父母出去散步,从家走了20分钟到一个离家900米的报亭;②母亲随即按原来的速度返回;③父亲在报亭看报10分钟;④然后父亲用15分钟返回家.
以上描述,符合函数图象的是( )
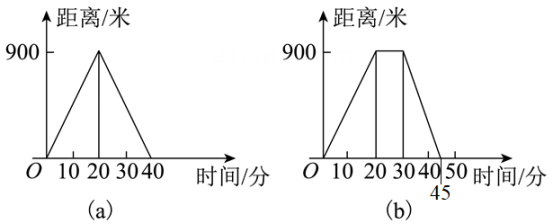 A、①③ B、②④ C、①②③ D、①②③④35. 声音在空气中传播的速度v(简称声速)与空气温度t的关系(如下表所示),则下列说法错误的是( )
A、①③ B、②④ C、①②③ D、①②③④35. 声音在空气中传播的速度v(简称声速)与空气温度t的关系(如下表所示),则下列说法错误的是( )温度t/℃
0
10
20
30
声速v/(m/s)
318
324
330
336
342
348
A、温度越高,声速越快 B、在这个变化过程中,自变量是声速t,t是v的函数 C、当空气温度为20℃,声速为342m/s D、声速v与温度t之间的关系式为