浙江省永康市2023年九年级数学中考适应性考试试卷
试卷更新日期:2023-05-23 类型:中考模拟
一、选择题(本题有10小题,每小题3分,共30分)
-
1. -2023的相反数是( )A、2023 B、 C、2023 D、2. 2022年我国新能源汽车销售量约为6887000辆,同比增长93.4%.数6887000用科学记数法表示为( )A、0.6887×107 B、6.887×106 C、6.887×107 D、68.87×1053. 由四个相同的小正方体搭成的几何体如图所示,它的俯视图是( )
 A、
A、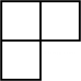 B、
B、 C、
C、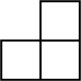 D、
D、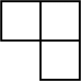 4. 二次根式中字母a的取值范围是( )A、a≠3 B、a>3 C、a≥3 D、a≥-35. 方程x2- 2x=1经过配方后,其结果正确的是( )A、(x-1)2=2 B、(x+1) 2=2 C、(x-1) 2=1 D、(x+1) 2=16. 某果园实验基地种植了甲、乙两个品种的葡萄树,工作人员随机从甲、乙两品种的葡萄树中采摘了10棵,统计了每棵的产量.下列关于两品种每棵产量的平均数和方差的描述中,能说明甲品种的葡萄产量较稳定的是( )A、 B、 C、 D、7. 一沙滩球网支架示意图如图所示,AB=AC=a米,∠ABC=a,则最高点A离地面BC的高度为( )
4. 二次根式中字母a的取值范围是( )A、a≠3 B、a>3 C、a≥3 D、a≥-35. 方程x2- 2x=1经过配方后,其结果正确的是( )A、(x-1)2=2 B、(x+1) 2=2 C、(x-1) 2=1 D、(x+1) 2=16. 某果园实验基地种植了甲、乙两个品种的葡萄树,工作人员随机从甲、乙两品种的葡萄树中采摘了10棵,统计了每棵的产量.下列关于两品种每棵产量的平均数和方差的描述中,能说明甲品种的葡萄产量较稳定的是( )A、 B、 C、 D、7. 一沙滩球网支架示意图如图所示,AB=AC=a米,∠ABC=a,则最高点A离地面BC的高度为( ) A、米 B、米 C、米 D、米8. 如图,小明分别以点A, B为圆心,大于线段AB长度一半的长为半径作弧,相交于点E,F,作直线EF分别交弦AB和劣弧AB于点C, D.小明量得AB=4cm, CD=1cm.则劣弧AB所在圆的半径长为( )
A、米 B、米 C、米 D、米8. 如图,小明分别以点A, B为圆心,大于线段AB长度一半的长为半径作弧,相交于点E,F,作直线EF分别交弦AB和劣弧AB于点C, D.小明量得AB=4cm, CD=1cm.则劣弧AB所在圆的半径长为( ) A、3cm B、2.5cm C、2cm D、2.4cm9. 如图,已知正五边形ABCDE的边长为2,连结对角线构成另一个正五边形FGHIJ,则正五边形FGHIJ的边长为( )
A、3cm B、2.5cm C、2cm D、2.4cm9. 如图,已知正五边形ABCDE的边长为2,连结对角线构成另一个正五边形FGHIJ,则正五边形FGHIJ的边长为( )
 A、1 B、 C、3- D、-110. 我们知道订书针的两条短边垂直长边.如图是由三枚完全相同的订书针ABCD,EFGH,IJKL拼成的图形,点B,E,C,F在同一条直线上,点D,K,L分别在JK,GF,HG上, 4B=CD=EF=GH=IJ=LK=1, BC=FG=JK=2.当点4, I重合时, HL的长度为( )
A、1 B、 C、3- D、-110. 我们知道订书针的两条短边垂直长边.如图是由三枚完全相同的订书针ABCD,EFGH,IJKL拼成的图形,点B,E,C,F在同一条直线上,点D,K,L分别在JK,GF,HG上, 4B=CD=EF=GH=IJ=LK=1, BC=FG=JK=2.当点4, I重合时, HL的长度为( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题有6小题,每小题4分,共24分)
-
11. 分解因式: a2-1=.12. 不等式组的解集是.13. 如图,电路图上有A,B, C三个开关和一个小灯泡,闭合开关C或同时闭合开关A和B都可使小灯泡发光.任意闭合其中一个开关,小灯泡发光的概率为.
 14. 《水浒传》中关于神行太保戴宗有这样一段描述:程途八百里,朝去暮还来.某日,戴宗去180里之外的地方打探情报,去时顺风,用了2小时;回来时逆风,用了6小时,则戴宗的速度为里/小时.15. 如图,已知△ABC和△ADE为等腰直角三角形,∠ACB-∠AED- 90°, AC= , AE= , 连结CE, BD.在△AED绕点A旋转的过程中,当直线CE垂直于AD时,BD=.
14. 《水浒传》中关于神行太保戴宗有这样一段描述:程途八百里,朝去暮还来.某日,戴宗去180里之外的地方打探情报,去时顺风,用了2小时;回来时逆风,用了6小时,则戴宗的速度为里/小时.15. 如图,已知△ABC和△ADE为等腰直角三角形,∠ACB-∠AED- 90°, AC= , AE= , 连结CE, BD.在△AED绕点A旋转的过程中,当直线CE垂直于AD时,BD=. 16. 如图1为一.款折叠婴儿车的演示过程.点D处有一卡扣,打开卡扣,从手柄P点处往下按压,完成折叠.已知支撑杆AB =AC= 60cm,BD= 30cm, 卡扣D恰好为BC中点,推杆PD=110cm.
16. 如图1为一.款折叠婴儿车的演示过程.点D处有一卡扣,打开卡扣,从手柄P点处往下按压,完成折叠.已知支撑杆AB =AC= 60cm,BD= 30cm, 卡扣D恰好为BC中点,推杆PD=110cm.

(结果均精确到0.1cm.参考数据:≈1.414,≈1.732, sin75°≈0.966, cos75°≈0.259,tan75°≈3.732,sin14.5°~0.250, cos14.5°~0.968, tan14.5°≈0.257. )
(1)、如图2,当卡扣D固定时,支撑杆AB与水平线l呈15°角, 手柄P到水平线l的距离约为cm.(2)、当折叠完成时,∠CDB=60°(如图3 所示),支撑杆AB与水平线l呈1°角,此时手柄P约下降了cm.三、解答题(本题有8小题, 共66分,)
-
17. 计算:|-1|-2cos30° ++(-2023)0 .18. 以下是小亮同学在解分式方程的过程:
解:去分母得x(x+2)-x+1=1……………………①
化简得x2 +x=0…………………………………②
解得x1= 0,x2=-1…………………………………③
经检验,x1=0,x2=-1是原方程的解……………④
所以原方程的解为x1=0,x2=-1
根据小亮的解题过程,回答下列问题:
(1)、小亮的解题过程中第步开始出现了错误.(2)、请你写出正确的解答过程.19. 如图,点B, F, C, E在同一直线上,AB=DE, ∠B=∠E,BF=CE. (1)、求证:△ABC≌△DEF.(2)、连结AF, CD,试判断四边形AFDC的形状,并说明理由.20. 某校为提高九年级学生的体育成绩,针对跳绳项目进行了专门训练.为了解训练效果,在训练前后各组织了- .次测试,并从中抽取了50名学生的数据制成了如下条形统计图,请回答下列问题:
(1)、求证:△ABC≌△DEF.(2)、连结AF, CD,试判断四边形AFDC的形状,并说明理由.20. 某校为提高九年级学生的体育成绩,针对跳绳项目进行了专门训练.为了解训练效果,在训练前后各组织了- .次测试,并从中抽取了50名学生的数据制成了如下条形统计图,请回答下列问题:某校九年级50名学生训练前后跳绳成绩条形统计图
 (1)、训练前成绩的中位数是分,训练后成绩的众数是分.(2)、训练后比训练前平均分增加了多少分?(3)、如果该校九年级有400名学生,那么估计训练后成绩为满分(10分)的人数有多少人?21. 如图,在平面直角坐标系中,曲线AB是反比例函数图象的一部分. 把曲线AB关于y轴对称,再向下平移m (m>0)个单位得到曲线CD,且点D恰好在直线AB上.已知点B的坐标为(-1,-3), A,B两点间的水平距离为2.
(1)、训练前成绩的中位数是分,训练后成绩的众数是分.(2)、训练后比训练前平均分增加了多少分?(3)、如果该校九年级有400名学生,那么估计训练后成绩为满分(10分)的人数有多少人?21. 如图,在平面直角坐标系中,曲线AB是反比例函数图象的一部分. 把曲线AB关于y轴对称,再向下平移m (m>0)个单位得到曲线CD,且点D恰好在直线AB上.已知点B的坐标为(-1,-3), A,B两点间的水平距离为2. (1)、求曲线AB所在的反比例函数的解析式.(2)、求m的值.22. 如图,△ABC内接于ʘO,AB为圆O的直径,点F在ʘO上,连结CF交AB于点E,延长CF至点D,连结AD.已知BC=CE=3,AB=9,∠DAF= ∠ACD.
(1)、求曲线AB所在的反比例函数的解析式.(2)、求m的值.22. 如图,△ABC内接于ʘO,AB为圆O的直径,点F在ʘO上,连结CF交AB于点E,延长CF至点D,连结AD.已知BC=CE=3,AB=9,∠DAF= ∠ACD. (1)、求证: AD为ʘO的切线.(2)、求△ABC的AB边上的高.(3)、求DF的长.23. 根据以下素材,探索完成任务.
(1)、求证: AD为ʘO的切线.(2)、求△ABC的AB边上的高.(3)、求DF的长.23. 根据以下素材,探索完成任务.运用二次函数来研究植物幼苗叶片的生长状况
素
材
在大自然里,有很
多数学的奥秘. 一片美
丽的心形叶片、一棵生
长的幼苗都可以看作
把一条抛物线的一部
分沿直线折叠而形成.

问题解决
任
务
1
确定心形叶片的形状
如图3建立平面直角坐标系,心形叶片下部轮廓线可
以看作是二次函数y=mx2-4mx- 20m+5图象的一部分,
且过原点,求抛物线的解析式及顶点D的坐标.

任
务
2
研究心形叶片的尺寸
如图3,心形叶片的对称轴直线y=x+ 2与坐标轴交于
A,B两点,直线x =6分别交抛物线和直线AB于点E, F,点E, E'是叶片上的一对对称点,EE'交直线AB与点G.求叶片此处的宽度EE'.
任
务
3
研;究幼苗叶片的生长
小李同学在观察幼苗生长的过程中,发现幼苗叶片下方轮廓线都可以看作是二次函数y=mx2-4mx - 20m+ 5图象的一部分,
如图4,幼苗叶片下方轮廓线正好对应任务1中的二次函数.已知直线PD与水平线的夹角为45° .三天后,点D长到与点P同一水平位置的点D'时,叶尖Q落在射线OP上(如图5所示).求此时幼苗叶子的长度和最大宽度.
 24. 如图1,在矩形ABCD中,AB=6,BC=6.对角线AC, BD相交于点O,点E, F分别在对角线AC,BD.上,CE=2AE, 连结EF.
24. 如图1,在矩形ABCD中,AB=6,BC=6.对角线AC, BD相交于点O,点E, F分别在对角线AC,BD.上,CE=2AE, 连结EF. (1)、求线段OE的长和∠AOB的度数.(2)、当点F在点B处时,以EF为边在右下方作等边△EFG,连结OG.在点F运动过程中,点G也随之运动.如图2,过点F作AB的平行线交AC于点H.若设线段BF长为x,线段OG长为y,求y关于x的函数关系式,并写出相应x的取值范围.(3)、若点F在直线BD上运动,以EF为边作等边△EFG.当点G恰好落在矩形ABCD的边上时,求FG的长.
(1)、求线段OE的长和∠AOB的度数.(2)、当点F在点B处时,以EF为边在右下方作等边△EFG,连结OG.在点F运动过程中,点G也随之运动.如图2,过点F作AB的平行线交AC于点H.若设线段BF长为x,线段OG长为y,求y关于x的函数关系式,并写出相应x的取值范围.(3)、若点F在直线BD上运动,以EF为边作等边△EFG.当点G恰好落在矩形ABCD的边上时,求FG的长.