浙江省温州市瓯海区2023年中考数学二模试卷
试卷更新日期:2023-05-23 类型:中考模拟
一、选择题(本大题共10小题,共40.0分。)
-
1. 下列4个数中最小的数是( )A、1 B、-3 C、0 D、2. 如图是由4个相同的正方体搭成的几何体,则其俯视图是( )
 A、
A、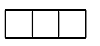 B、
B、 C、
C、 D、
D、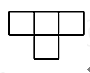 3. 如图,是九(1)班45名同学每周课外阅读时间的频数分布直方图每组含前一个边界值,不含后一个边界值 , 由图可知,每周课外阅读时间不小于6小时的人数是( )
3. 如图,是九(1)班45名同学每周课外阅读时间的频数分布直方图每组含前一个边界值,不含后一个边界值 , 由图可知,每周课外阅读时间不小于6小时的人数是( ) A、6人 B、8人 C、14人 D、36人4. 将抛物线先向左平移1个单位,再向下平移2个单位,所得抛物线的表达式为( )A、 B、 C、 D、5. 如图,在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是( )
A、6人 B、8人 C、14人 D、36人4. 将抛物线先向左平移1个单位,再向下平移2个单位,所得抛物线的表达式为( )A、 B、 C、 D、5. 如图,在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是( ) A、 B、 C、 D、6. 某企业今年1月份产值为万元,2月份比1月份减少了10%,3月份比2月份增加了15%,则3月份的产值是( )A、万元 B、万元 C、万元 D、万元7. 如图,已知 , 分别是的 , 边上的点, , 且那么:等于( )
A、 B、 C、 D、6. 某企业今年1月份产值为万元,2月份比1月份减少了10%,3月份比2月份增加了15%,则3月份的产值是( )A、万元 B、万元 C、万元 D、万元7. 如图,已知 , 分别是的 , 边上的点, , 且那么:等于( ) A、2:3 B、1:2 C、1:3 D、1:48. 在平面直角坐标系中,过点的直线经过一、二、三象限,若点 , , 都在直线1上,则下列判断正确的是( )A、 B、 C、 D、9. 六一儿童节到了,小亮在图纸上先画一个边长为的正方形,再以该正方形的四个顶点为圆心,长为半径作弧,则图中实线所表示的饰品轮廓长为( )
A、2:3 B、1:2 C、1:3 D、1:48. 在平面直角坐标系中,过点的直线经过一、二、三象限,若点 , , 都在直线1上,则下列判断正确的是( )A、 B、 C、 D、9. 六一儿童节到了,小亮在图纸上先画一个边长为的正方形,再以该正方形的四个顶点为圆心,长为半径作弧,则图中实线所表示的饰品轮廓长为( ) A、 B、 C、 D、10. 如图,在给定的正方形中,点从点出发,沿边方向向终点运动,交于点 , 以 , 为邻边构造▱ , 连接 , 则的度数的变化情况是( )
A、 B、 C、 D、10. 如图,在给定的正方形中,点从点出发,沿边方向向终点运动,交于点 , 以 , 为邻边构造▱ , 连接 , 则的度数的变化情况是( ) A、一直减小 B、一直减小后增大 C、一直增大 D、先增大后减小
A、一直减小 B、一直减小后增大 C、一直增大 D、先增大后减小二、填空题(本大题共6小题,共30.0分)
-
11. 分解因式: .
12. 二次根式有意义,则的取值范围是 .13. 在“争创美丽校园,争做文明学生”示范校评比活动中,10位评委给某校的评分情况下表所示:评分(分)
80
85
90
95
评委人数
1
2
5
2
则这10位评委评分的平均数是 分.
14. 如图, , 是半圆上的两点,是直径若 , 则 度 15. 如图,线段轴,双曲线与分别经过点 , 点 , 过点作轴的垂线段,垂足为 , 连接 , 与相交于点 , 若 , 则:的值为 .
15. 如图,线段轴,双曲线与分别经过点 , 点 , 过点作轴的垂线段,垂足为 , 连接 , 与相交于点 , 若 , 则:的值为 . 16. 在一次美术课堂的剪纸活动中,小刚把一张菱形的纸片沿着各边的中点,剪取四边形 , 纸片分别沿、折叠使得点落在 , 点落在处,且直线与直线重合,满足 , 若阴影部分的周长之和等于16, , 求的值是 .
16. 在一次美术课堂的剪纸活动中,小刚把一张菱形的纸片沿着各边的中点,剪取四边形 , 纸片分别沿、折叠使得点落在 , 点落在处,且直线与直线重合,满足 , 若阴影部分的周长之和等于16, , 求的值是 .
三、解答题(本大题共8小题,共80.0分。)
-
17.(1)、计算:;(2)、化简: .18. 如图,已知E、F分别是▱ABCD的边BC、AD上的点,且BE=DF.
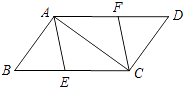 (1)、求证:四边形AECF是平行四边形;(2)、若四边形AECF是菱形,且BC=10,∠BAC=90°,求BE的长.19. 如图甲,图乙是两张形状、大小完全相同的方格纸,方格纸中的两个小正方形的边长均为1,请按要求画出以为对角线的格点四边形要求所作的四边形各顶点都在格点上 .
(1)、求证:四边形AECF是平行四边形;(2)、若四边形AECF是菱形,且BC=10,∠BAC=90°,求BE的长.19. 如图甲,图乙是两张形状、大小完全相同的方格纸,方格纸中的两个小正方形的边长均为1,请按要求画出以为对角线的格点四边形要求所作的四边形各顶点都在格点上 . (1)、在图甲中所画四边形至少有三边相等,且点要落在四边形内部不包括边界上;(2)、在图乙中所画四边形至少有两个角等于 , 且点要落在四边形外部.20. 随着春天气温变暖,某校组织同学们分别到、、、四个景点进行春游活动,学校把学生前往四个地方的人数做了统计,得到下列两幅不完整的统计图,如图所示:
(1)、在图甲中所画四边形至少有三边相等,且点要落在四边形内部不包括边界上;(2)、在图乙中所画四边形至少有两个角等于 , 且点要落在四边形外部.20. 随着春天气温变暖,某校组织同学们分别到、、、四个景点进行春游活动,学校把学生前往四个地方的人数做了统计,得到下列两幅不完整的统计图,如图所示: (1)、本次参加春游活动学生总人数有 人,在扇形统计图中,去景点活动的人数对应扇形的圆心角的度数是 度;(2)、请你将条形统计图补充完整;(3)、本次春游活动中,学校分配给九年级学生甲、乙、丙三辆车,小明与小华都可以从这三辆车中任选一辆搭乘,求小明与小华同车的概率要求画出树状图或列表 .21. 如图,已知是的直径, , 弦与交于点 , 过点、分别作的切线交于点 , 与延长线交于点 .
(1)、本次参加春游活动学生总人数有 人,在扇形统计图中,去景点活动的人数对应扇形的圆心角的度数是 度;(2)、请你将条形统计图补充完整;(3)、本次春游活动中,学校分配给九年级学生甲、乙、丙三辆车,小明与小华都可以从这三辆车中任选一辆搭乘,求小明与小华同车的概率要求画出树状图或列表 .21. 如图,已知是的直径, , 弦与交于点 , 过点、分别作的切线交于点 , 与延长线交于点 . (1)、求证:;(2)、若:: , 且 , 求的长.22. 某校计划到市场购买、两种品牌的足球,购买种品牌的足球50个,种品牌的足球25个,共花费4500元,已知购买一个种品牌的足球比购买一个种品牌的足球多花30元.(1)、求购买一个种品牌,一个种品牌的足球各需多少元?(2)、学校为了响应“足球进校园”的号召,决定再次购进、两种品牌足球共50个,正好赶上商场对商品价格进行调整,品牌足球销售单价比第一次购买时提高4元,品牌足球按第一次购买时售价的9折出售,如果学校此次购买、两种品牌足球的总费用不超过第一次花费的65%,则第二次购买种足球至少多少个.23. 如图,与轴交于点 , 与轴的正半轴交于点 , 过点作轴交抛物线于另一点 , 点在轴的负半轴上,连接交轴于点 , 若 .
(1)、求证:;(2)、若:: , 且 , 求的长.22. 某校计划到市场购买、两种品牌的足球,购买种品牌的足球50个,种品牌的足球25个,共花费4500元,已知购买一个种品牌的足球比购买一个种品牌的足球多花30元.(1)、求购买一个种品牌,一个种品牌的足球各需多少元?(2)、学校为了响应“足球进校园”的号召,决定再次购进、两种品牌足球共50个,正好赶上商场对商品价格进行调整,品牌足球销售单价比第一次购买时提高4元,品牌足球按第一次购买时售价的9折出售,如果学校此次购买、两种品牌足球的总费用不超过第一次花费的65%,则第二次购买种足球至少多少个.23. 如图,与轴交于点 , 与轴的正半轴交于点 , 过点作轴交抛物线于另一点 , 点在轴的负半轴上,连接交轴于点 , 若 . (1)、用含的代数式表示的长;(2)、当时,判断点是否落在抛物线上,并说明理由;(3)、过点作轴交轴于点 , 延长至 , 使得 , 连接交轴于点 , 连接交轴于点 , 若的面积与的面积相等,求的值.24. 如图 , 在中, , , , 点在上, , 动点从点出发沿线段以每秒1个单位的速度运动,过点作 , 交射线于点 , 点关于点的对称点为 , 以为边在上方作正方形 , 设点运动的时间为秒 .
(1)、用含的代数式表示的长;(2)、当时,判断点是否落在抛物线上,并说明理由;(3)、过点作轴交轴于点 , 延长至 , 使得 , 连接交轴于点 , 连接交轴于点 , 若的面积与的面积相等,求的值.24. 如图 , 在中, , , , 点在上, , 动点从点出发沿线段以每秒1个单位的速度运动,过点作 , 交射线于点 , 点关于点的对称点为 , 以为边在上方作正方形 , 设点运动的时间为秒 .
 (1)、当点在线段上时,求的长用含的代数式表示;(2)、当正方形的顶点或刚好落在在的边上时,求的值;(3)、如图2,以为直径作 , 当与的边所在的直线相切时,请求出所有满足条件的的值.
(1)、当点在线段上时,求的长用含的代数式表示;(2)、当正方形的顶点或刚好落在在的边上时,求的值;(3)、如图2,以为直径作 , 当与的边所在的直线相切时,请求出所有满足条件的的值.