浙江省金华市金东区2023年中考二模数学试题
试卷更新日期:2023-05-23 类型:中考模拟
一、仔细选一选(本大题有10小题,每小题3分,共30分.)
-
1. 实数2,0, , -0.4中,最小的数是( )A、2 B、0 C、 D、-0.42. 若长度分别为a,2,3的三条线段能组成一个三角形,则a的值可能是( )A、1 B、2 C、5 D、83. 金华市2022年全市地区生产总值(GDP)约为55562.47亿元,其中数55562.47用科学记数法表示为( )A、 B、 C、 D、4. 公园里有一种供游客休息的石板凳如图所示,它的左视图是( )
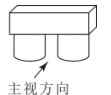 A、
A、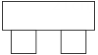 B、
B、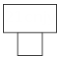 C、
C、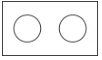 D、
D、 5. 如图,△ABC和△DEF中, , , 点B,E,C,F共线,添加一个条件,不能判断的是( )
5. 如图,△ABC和△DEF中, , , 点B,E,C,F共线,添加一个条件,不能判断的是( )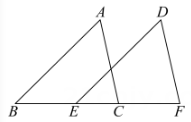 A、 B、 C、 D、6. 在一个不透明的袋子里,装有3个红球、2个白球,它们除颜色外都相同,从袋中任意摸出一个球为红球的概率是( )A、 B、 C、 D、7. 我国在清朝时期的课本中用“”来表示代数式 , 那么“”的化简结果是( )A、 B、 C、 D、8. 如图,将5个大小相同的长方形置于平面直角坐标系中,若顶点 , , 则顶点的坐标是( )
A、 B、 C、 D、6. 在一个不透明的袋子里,装有3个红球、2个白球,它们除颜色外都相同,从袋中任意摸出一个球为红球的概率是( )A、 B、 C、 D、7. 我国在清朝时期的课本中用“”来表示代数式 , 那么“”的化简结果是( )A、 B、 C、 D、8. 如图,将5个大小相同的长方形置于平面直角坐标系中,若顶点 , , 则顶点的坐标是( ) A、 B、 C、 D、9. 如图,小明在C处看到西北方向上有一凉亭A,北偏东35°的方向上有一棵大树B,已知凉亭A在大树B的正西方向,若米,则AB的长等于( )
A、 B、 C、 D、9. 如图,小明在C处看到西北方向上有一凉亭A,北偏东35°的方向上有一棵大树B,已知凉亭A在大树B的正西方向,若米,则AB的长等于( )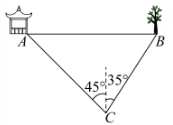 A、 B、 C、 D、10. 如图,在正六边形ABCDEF中, , 点O在对角线AD上, , 以O为圆心,OB为半径画弧,分别交AB,AF于点M,N.则的长为( )
A、 B、 C、 D、10. 如图,在正六边形ABCDEF中, , 点O在对角线AD上, , 以O为圆心,OB为半径画弧,分别交AB,AF于点M,N.则的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题有6小题,每小题4分,共24分)
-
11. 因式分解: .12. 若分式有意义,则x的取值范围是 .13. 在“预防溺水”专题教育活动中,902班开展了预防溺水知识有奖竞答活动,以下公布的是某5位同学的竞答成绩(分):90,78,82,85,90,这组数据的中位数是 .14. 如图,在△ABC中,∠ABC=90°,将△ABC沿AB方向平移AD的长度得到△DEF,EF=8,BE=3,CB与DF交于点G,CG=3,则图中阴影部分的面积为 .
 15. 如图,点G是正方形ABCD边AB上的一点,连结CG,过点C作 , 交AD的延长线于点E,过点E作 , 过点G作 , EF和GF交于点F,延长CD交EF于点H,连结GH,以HD和DA为边作矩形ADHI.记的面积为 , 的面积为 , 矩形ADHI的面积为 , 若 , , 则 .
15. 如图,点G是正方形ABCD边AB上的一点,连结CG,过点C作 , 交AD的延长线于点E,过点E作 , 过点G作 , EF和GF交于点F,延长CD交EF于点H,连结GH,以HD和DA为边作矩形ADHI.记的面积为 , 的面积为 , 矩形ADHI的面积为 , 若 , , 则 . 16. 如图,一个立方体有盖盒子,棱长为8cm,当正方形PDCS合上时,点A与点P重合,点B与点S重合,此时,两个全等的长方形ADFE与长方形BCHG向内合上,且顶点E,G都落在AB边上,点E在点G的右侧, .
16. 如图,一个立方体有盖盒子,棱长为8cm,当正方形PDCS合上时,点A与点P重合,点B与点S重合,此时,两个全等的长方形ADFE与长方形BCHG向内合上,且顶点E,G都落在AB边上,点E在点G的右侧, .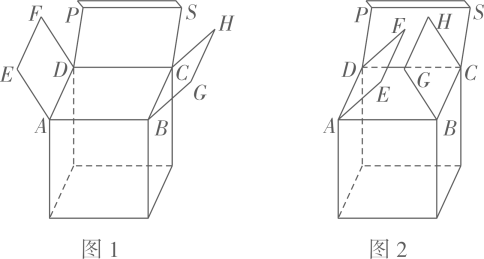 (1)、AE的长度是cm.(2)、长方形ADFE和长方形BCHG,从底面ABCD翻开的过程中,当且∠EAB最大时,∠EAB的余弦值为 .
(1)、AE的长度是cm.(2)、长方形ADFE和长方形BCHG,从底面ABCD翻开的过程中,当且∠EAB最大时,∠EAB的余弦值为 .三、解答题(本题有8小题,共66分)
-
17. 计算:18. 解不等式组:19. 如图, , 点E是BA延长线上一点, .
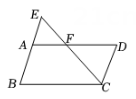 (1)、求证: .(2)、若CE平分∠BCD,∠E=47°,求∠B的度数.20. 为了丰富初中学生的大课间活动,某区教育局要求各学校开展形式多样的阳光体育活动,某中学随机抽取了本校部分学生对“最喜欢的体育运动项目”进行问卷调查,要求每位同学必须选一项且只能选一项,得到如下两幅不完整的条形统计图和扇形统计图,请根据图中信息回答下列问题:
(1)、求证: .(2)、若CE平分∠BCD,∠E=47°,求∠B的度数.20. 为了丰富初中学生的大课间活动,某区教育局要求各学校开展形式多样的阳光体育活动,某中学随机抽取了本校部分学生对“最喜欢的体育运动项目”进行问卷调查,要求每位同学必须选一项且只能选一项,得到如下两幅不完整的条形统计图和扇形统计图,请根据图中信息回答下列问题: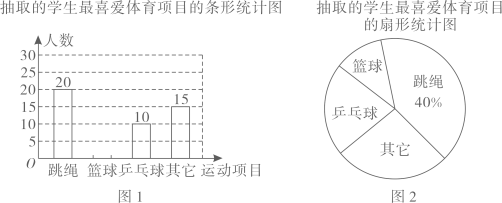 (1)、在这次调查中,①求调查的总人数.②求在扇形统计图中的“其它”部分的圆心角度数.(2)、请将条形统计图补充完整.(3)、已知该校共有900名学生,请估计该校最喜欢乒乓球项目的学生人数.21. 某气球内充满一定质量的气体.通过测量,当温度不变时,该气球内气体的压强p(kPa)和气体体积V(m3)的几组对应值如下表.
(1)、在这次调查中,①求调查的总人数.②求在扇形统计图中的“其它”部分的圆心角度数.(2)、请将条形统计图补充完整.(3)、已知该校共有900名学生,请估计该校最喜欢乒乓球项目的学生人数.21. 某气球内充满一定质量的气体.通过测量,当温度不变时,该气球内气体的压强p(kPa)和气体体积V(m3)的几组对应值如下表.p(kPa)
0.6
0.8
1.0
1.2
1.4
V(m3)
150.4
112.5
90.0
75.1
64.3
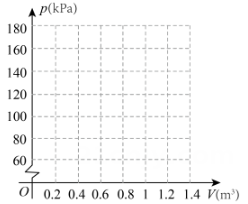 (1)、根据表中的数据画出函数图象,并求出压强p(kPa)关于体积V(m3)的函数表达式.(函数表达式中的数值精确到单位1)(2)、当气体体积为2m3时,气球内气体的压强是多少?(3)、当气球内气体的压强大于180kpa时,气球就会爆炸.请问气体的体积应不小于多少时,气球才不会爆炸.22. 如图,已知AB,CD是⊙O的直径,点E是CA延长线的一点,射线ED交⊙O点于F,连结AD,CF,∠CDA=∠EDA,∠CAB=30°,AB=8.
(1)、根据表中的数据画出函数图象,并求出压强p(kPa)关于体积V(m3)的函数表达式.(函数表达式中的数值精确到单位1)(2)、当气体体积为2m3时,气球内气体的压强是多少?(3)、当气球内气体的压强大于180kpa时,气球就会爆炸.请问气体的体积应不小于多少时,气球才不会爆炸.22. 如图,已知AB,CD是⊙O的直径,点E是CA延长线的一点,射线ED交⊙O点于F,连结AD,CF,∠CDA=∠EDA,∠CAB=30°,AB=8.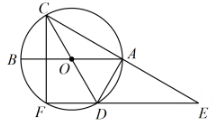 (1)、求证: .(2)、求∠FCA的度数.(3)、求CE的长.23. 定义:若n为常数,当一个函数图象上存在横、纵坐标和为n的点,则称该点为这个函数图象关于n的“恒值点”,例如:点(1,2)是函数图象关于3的“恒值点”.
(1)、求证: .(2)、求∠FCA的度数.(3)、求CE的长.23. 定义:若n为常数,当一个函数图象上存在横、纵坐标和为n的点,则称该点为这个函数图象关于n的“恒值点”,例如:点(1,2)是函数图象关于3的“恒值点”. (1)、判断点(1,3),(2,8),(3,7)是否为函数图象关于10的“恒值点”.(2)、如图1,抛物线与x轴交于A,B两点(A在B的左侧),现将抛物线在x轴下方的部分沿x轴翻折,抛物线的其余部分保持不变,所得的新图象如图2所示.
(1)、判断点(1,3),(2,8),(3,7)是否为函数图象关于10的“恒值点”.(2)、如图1,抛物线与x轴交于A,B两点(A在B的左侧),现将抛物线在x轴下方的部分沿x轴翻折,抛物线的其余部分保持不变,所得的新图象如图2所示.Ⅰ.求翻折后A,B之间的抛物线解析式.(不必写出x的取值范围)
Ⅱ.当新图象上恰好有3个关于c的“恒值点”时,请用含b的代数式表示c.
24. 如图1,在矩形ABCD中,AB=4,BC=5,动点P从点C出发,以1个单位每秒速度,沿线段CD运动,同时,动点Q从点B出发,以2个单位每秒速度,沿射线BC运动,当点P到达点D时,点P,Q同时停止运动,设运动时间为t秒.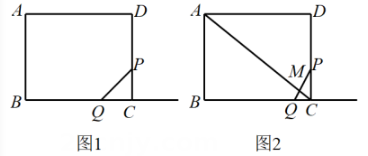 (1)、请用含t的代数式表示线段CQ的长.(2)、如图2,AC与PQ交于点M,当时,求△PMC与△QMC的面积之比.(3)、在点P,Q的整个运动过程中,直线AC上是否存在点E,使以PE为直角边的Rt△PQE,与以点P,Q,C三点为顶点的三角形相似?若不存在,说明理由;若存在,求t的值.
(1)、请用含t的代数式表示线段CQ的长.(2)、如图2,AC与PQ交于点M,当时,求△PMC与△QMC的面积之比.(3)、在点P,Q的整个运动过程中,直线AC上是否存在点E,使以PE为直角边的Rt△PQE,与以点P,Q,C三点为顶点的三角形相似?若不存在,说明理由;若存在,求t的值.