湖北省襄阳市枣阳市2023年中考一模数学试题

试卷更新日期：2023-05-23 类型：中考模拟

进入出卷网下载

一、选择题（本大题共10个小题，每小题3分，共30分）

1. 实数－3的绝对值是（）

A、3 B、－3 C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
2. 某几何体的三视图如左图所示，则该几何体是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是（）

A、 $x^{3} \cdot x^{4} = x^{12}$ B、 ${(x^{3})}^{3} = x^{6}$ C、 ${(3 x)}^{2} = 9 x^{2}$ D、 $2 x^{2} \div x = x$

查看试题解析
4. 如图，直线 $l_{1} ∥ l_{2}$ ，直线 $l_{3}$ 与 $l_{1}$ ， $l_{2}$ 分别交于点 $A$ ， $C$ ， $B C ⊥ l_{3}$ 交 $l_{1}$ 于点 $B$ ，若 $∠ 1 = 70 °$ ，则 $∠ 2$ 的度数为（）

A、10° B、20° C、30° D、40°

查看试题解析
5. 我国古代数学著作《孙子算经》有“多人共车”问题：“今有三人共车，二车空；二人共车，九人步.问：人与车各几何?”其大意如下：有若干人要坐车，如果每3人坐一辆车，那么有2辆空车；如果每2人坐一辆车，那么有9人需要步行，问人与车各多少?设共有 $x$ 人， $y$ 辆车，则可列方程组为（）

A、 ${\begin{array}{l} 3 (y - 2) = x \\ 2 y - 9 = x \end{array}$ B、 ${\begin{array}{l} 3 (y + 2) = x \\ 2 y + 9 = x \end{array}$ C、 ${\begin{array}{l} 3 (y - 2) = x \\ 2 y + 9 = x \end{array}$ D、 ${\begin{array}{l} 3 (y - 2) = x \\ 2 y + x = 9 \end{array}$

查看试题解析
6. 如图，在▱ABCD中，BM是∠ABC的平分线交CD于点M，且MC=2，▱ABCD的周长是14，则DM等于（）

A、1 B、2 C、3 D、4

查看试题解析
7. 下列事件中，属于必然事件的是（）

A、掷一次骰子，向上一面的点数是3 B、在平面上画一个矩形，这个矩形一定是轴对称图形 C、在一副扑克牌中抽取一张牌，抽出的牌是黑桃A D、射击运动员射击一次命中靶心

查看试题解析
8. 关于反比例函数 $y = - \frac{2}{x}$ ，下列说法正确的是（）

A、图象经过点 $(1 ， 2)$ B、图象位于第一、第三象限 C、当 $x_{2} > x_{1}$ 时， $y_{1} > y_{2}$ D、当 $x < 0$ 时，y随x的增大而增大

查看试题解析
9. 矩形具有而菱形不具有的性质是（　　）

A、对角线相等 B、对角线平分一组对角 C、对角线互相平分 D、对角线互相垂直

查看试题解析
10. 一次函数 $y = a x + 1$ 与反比例函数 $y = - \frac{a}{x}$ 在同一坐标系中的大致图象是（）

A、 B、 C、 D、

查看试题解析

二、填空题（本大题共6个小题，每小题3分，共18分）

11. 2023年春节假期，襄阳旅游市场强劲复苏，实现了爆发式增长，全市共接待游客4127300人次，较2022年同比增长28.03%．将数字4127300用科学记数法表示为．

查看试题解析
12. 不等式组 ${\begin{cases} 2 - x \geq 3 \\ \frac{3}{2} x + 1 > x - \frac{3}{2} \end{cases}$ 的解集是．

查看试题解析
13. 即将举行的第19届杭州亚运会的三个吉祥物分别取名“琼琮”“宸宸”“莲莲”．小明将三张正面分别印有以上3个吉祥物图案的卡片（卡片的形状、大小、质地都相同）背面朝上、洗匀．若先从中任意抽取1张，记录后放回，洗匀，再从中任意抽取1张，则两次抽取的卡片图案相同的概率是．

查看试题解析
14. 从地面竖直向上抛出一小球，小球的高度h（单位：米）与小球运动时间t（单位：秒）的函数关系式是 $h = 9.8 t - 49 t^{2}$ ．小球抛出秒后开始下落．

查看试题解析
15. $⊙ O$ 的半径是13cm，AB，CD是 $⊙ O$ 的两条弦，且 $A B ∥ C D$ ， $A B = 24 c m$ ， $C D = 10 c m$ ，则AB与CD之间的距离是．

查看试题解析
16. 如图，在正方形ABCD的对角线AC上取一点E，使得 $A E = 2 C E$ ，连接BE，将 $△ B C E$ 沿BE翻折得到 $△ B F E$ ，连接DF．若 $B C = 5$ ，则DF的长为．

查看试题解析

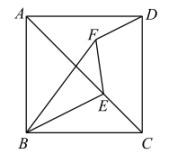
三、解答题（本大题共9个小题，共72分）

17. 先化简，再求值： $(a - \frac{2 a b - b^{2}}{a}) \div \frac{a^{2} - b^{2}}{a}$ ，其中 $a = 2 \sqrt{2} - 1$ ， $b = 1 - \sqrt{2}$ ．

查看试题解析

18. 某学校为了解该校七、八两个年级的学生对垃圾分类知识的掌握情况，决定从七、八年级各随机抽取20名学生进行垃圾分类知识测试，满分100分，成绩整理分析过程如下：

【收集数据】七年级20名学生测试成绩统计如下：56，58，64，67，69，70，70，71，74，77，78，78，84，86，86，86，86，91，92，95．

【整理、描述数据】七年级20名学生测试成绩频数分布直方图（每组数据包括左端值不包括右端值，如最左边第一组的成绩范围为 $50 \leq x < 60$ ）：

八年级20名学生测试成绩频数分布表：

成绩	$50 \leq x < 60$	$60 \leq x < 70$	$70 \leq x < 80$	$80 \leq x < 90$	$90 \leq x \leq 100$
人数	0	4	5	x	4

【分析数据】两组样本数据的平均数、中位数、众数方差如表所示：

年级	平均数	中位数	众数	方差
七年级	76.9	a	b	119.89
八年级	79.2	81	74	100.4

根据以上提供的信息，解答下列问题：

(1)、补全七年级20名学生测试成绩频数分布直方图；

(2)、统计表中，

x =

，

a =

，

b =

；

(3)、从样本数据分析看，分数较整齐的是年级；（填“七”或“八”）．

(4)、如果该校七年级、八年级各有500名学生，估计全校七年级垃圾分类知识测试成绩在80分及以上的有人；

查看试题解析

19. 图1是某种路灯的实物图，图2是该路灯的平面示意图．MN为立柱的一部分，灯臂AC，支架BC与立柱MN分别交于点A，B，灯臂AC与支架BC交于点C．已知 $∠ M A C = 58 °$ ， $∠ A C B = 28 °$ ， $B C = 60 c m$ ，求灯臂AC的长．（结果精确到1cm；参考数据： $s i n 58 ° \approx 0.85$ ， $c o s 58 ° \approx 0.53$ ， $t a n 58 ° \approx 1.60$ ）

查看试题解析
20. 如图，在矩形ABCD中，对角线AC，BD相交于点O， $A E ⊥ B D$ 于点E．

(1)、过点C作 $C F ⊥ B D$ 于点F（尺规作图，不写作法，保留作图痕迹）；

(2)、求证 $O E = O F$ ．

查看试题解析
21. 已知关于x的一元二次方程 $x^{2} - (k - 1) x + \frac{1}{4} k^{2} + 1 = 0$ ．

(1)、当k为何值时，方程有两个实数根；

(2)、若方程的两个根分别为m，n，满足 $(m - 1) (n - 1) = 11$ ，求k的值．

查看试题解析
22. 如图， $⊙ O$ 是 $△ A B C$ 的外接圆，AB为直径，∠BAC的平分线交 $⊙ O$ 于点D，交BC于点G，过点D作 $D E ⊥ A C$ 分别交AC，AB的延长线于点E，F．

(1)、求证：EF是 $⊙ O$ 的切线；

(2)、若 $B C = 4 \sqrt{3}$ ， $C E = 2$ ，求劣弧AC的长．

查看试题解析
23. 某体育用品专卖店计划购进A，B两种型号的篮球共100个．已知A型、B型篮球的进价和售价如下表所示：
型号
进价（元/个）
售价（元/个）
A型
120
销量不超过40个的部分
销量超过40个的部分
150
超过部分打九折
B型
100
120
A型篮球购进数量不少于25个不多于60个．设A型篮球的销售总金额为W元，A型篮球的销量为x个．

(1)、直接写出W与x之间的函数关系式及x的取值范围；

(2)、假设该专卖店购进的100个A，B两种型号的篮球全部售完，总获利为y元．求y与x之间的函数关系式，并求该专卖店购进A型，B型篮球各多少个时，才能使获得的总利润最大？最大利润为多少元？

(3)、为回馈社会，鼓励人民群众积极参加体育锻炼，在（2）中获得最大利润的进货方案下，该专卖店决定每销售一个A型、B型篮球分别拿出2m元和m元，捐赠给某体育公益基金会．若这100个篮球全部售出后所获总利润不低于2120元，求m的最大值．

查看试题解析
24. 【问题情境】 $△ A B C$ 和 $△ A P D$ 是共顶点的两个三角形，点P是边BC上一个动点（不与B重合），且 $∠ A P D = ∠ B$ ， $∠ P A D = ∠ B A C$ ，连接CD．

(1)、【特例分析】
如图①，当 $∠ P A D = ∠ B A C = 90 °$ ， $\frac{A B}{A C} = 1$ 时．猜想PB与CD之间的数量关系，并说明理由；并求出∠ACD的度数．

(2)、【拓展探究】
如图②，当 $∠ P A D = ∠ B A C = 90 °$ ， $\frac{A B}{A C} = k$ 时．请判断∠ACD与∠B的数量关系以及PB与CD之间的数量关系，并说明理由．

(3)、【学以致用】
如图③，当 $∠ A P D = ∠ B = 45 °$ ， $A B = 4 \sqrt{2}$ ， $B C = 12$ ， $A P = 5$ 时，求CD的长．

查看试题解析
25. 如图，平面直角坐标系中点A，B的坐标分别为 $(- 4 ， 0)$ ， $(2 ， 3)$ ，顶点为D的拋物线 $y = a x^{2} - 2 a x + 2$ 交y轴于点C．

(1)、如图，若 $a = 1$ 时．
①直接写出抛物线的解析式、直线AB的解析式，求出点C，D的坐标；

②当 $2 m - 1 \leq x \leq m + 1$ 时，y的最大值为3，求m的值；

(2)、当抛物线与线段AB有两个交点时，求a的取值范围．

查看试题解析

型号	进价（元/个）	售价（元/个）
A型	120	销量不超过40个的部分	销量超过40个的部分
		150	超过部分打九折
B型	100	120