湖北省襄阳市南漳县2023年中考模拟预测数学试题
试卷更新日期:2023-05-23 类型:中考模拟
一、选择题(共10小题,满分30分,每小题3分)
-
1. 如图所示,五个大小相同的正方体搭成的几何体,其左视图是( )
 A、
A、 B、
B、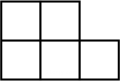 C、
C、 D、
D、 2. cos60°的值等于( )A、 B、 C、 D、3. 若点A(a-1,y1),B(a+1,y2)在反比例函数的图象上,且y1>y2 , 则a的取值范围是( )A、a<-1 B、-1<a<1 C、a>1 D、a<-1或a>14. 反比例函数的图象过(3,6),则k的值为( )A、15 B、18 C、21 D、255. 已知点(2,y1),(3,y2)在反比例函数的图象上,则下列结论正确的是( )A、y1>y2 B、y1<y2 C、y1=y2 D、y1和y2的大小不能确定6. 若点A(x1 , -2),B(x2 , 2),C(x3 , 6)都在反比例函数的图象上,则x1 , x2 , x3的大小关系是( )A、x2<x3<x1 B、x1<x3<x2 C、x1<x2<x3 D、x3<x1<x27. 如图是反比例函数的图象,则一次函数y=kx-2的图象大致是( )
2. cos60°的值等于( )A、 B、 C、 D、3. 若点A(a-1,y1),B(a+1,y2)在反比例函数的图象上,且y1>y2 , 则a的取值范围是( )A、a<-1 B、-1<a<1 C、a>1 D、a<-1或a>14. 反比例函数的图象过(3,6),则k的值为( )A、15 B、18 C、21 D、255. 已知点(2,y1),(3,y2)在反比例函数的图象上,则下列结论正确的是( )A、y1>y2 B、y1<y2 C、y1=y2 D、y1和y2的大小不能确定6. 若点A(x1 , -2),B(x2 , 2),C(x3 , 6)都在反比例函数的图象上,则x1 , x2 , x3的大小关系是( )A、x2<x3<x1 B、x1<x3<x2 C、x1<x2<x3 D、x3<x1<x27. 如图是反比例函数的图象,则一次函数y=kx-2的图象大致是( )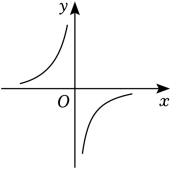 A、
A、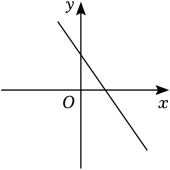 B、
B、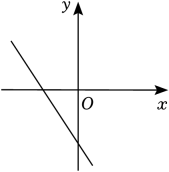 C、
C、 D、
D、 8. 如图,在平行四边形ABCD中,E,F是BC的三等分点,G是AD的中点,AF,EG交于点H,则=( )
8. 如图,在平行四边形ABCD中,E,F是BC的三等分点,G是AD的中点,AF,EG交于点H,则=( )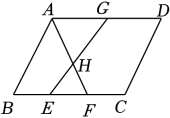 A、 B、 C、 D、9. 如图,在矩形ABCD中,AB<BC,连接AC,分别以点A,C为圆心,大于的长为半径画弧,两弧交于点M,N,直线MN分别交AD,BC于点E,F.下列结论中错误的是( )
A、 B、 C、 D、9. 如图,在矩形ABCD中,AB<BC,连接AC,分别以点A,C为圆心,大于的长为半径画弧,两弧交于点M,N,直线MN分别交AD,BC于点E,F.下列结论中错误的是( ) A、四边形AECF是菱形 B、∠AFB=2∠ACB C、AC•EF=CF•CD D、若AF平分∠BAC,则CF=2BF10. 如图,△ABC中,∠ABC=90°, , D是AB中点,P是以A为圆心,以AD为半径的圆上的动点,连接PB、PC,则 的最大值为( )
A、四边形AECF是菱形 B、∠AFB=2∠ACB C、AC•EF=CF•CD D、若AF平分∠BAC,则CF=2BF10. 如图,△ABC中,∠ABC=90°, , D是AB中点,P是以A为圆心,以AD为半径的圆上的动点,连接PB、PC,则 的最大值为( )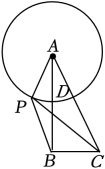 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(共5小题,满分20分,每小题4分)
-
11. 已知点A(1,-3)在反比例函数的图象上,则实数k的值为 .12. 如图,A是双曲线上的一点,点C是AO的中点,过点C作y轴的垂线,垂足为D,交双曲线于点B,则△ABD的面积是 .
 13. 已知点P(m,n)在双曲线上 , 则m2-3mn+n2的最小值为 .14. 如图,点D在△ABC的AD边上,且AD:AB=2:5,过点D作DE∥BC,交AC于点E,连接BE,则△ABE与△BEC的面积之比为 .
13. 已知点P(m,n)在双曲线上 , 则m2-3mn+n2的最小值为 .14. 如图,点D在△ABC的AD边上,且AD:AB=2:5,过点D作DE∥BC,交AC于点E,连接BE,则△ABE与△BEC的面积之比为 . 15. 如图,在矩形ABCD中,E是BC上一点,且AE⊥BD,若AB=3,AD=4,则BE的长为 .
15. 如图,在矩形ABCD中,E是BC上一点,且AE⊥BD,若AB=3,AD=4,则BE的长为 .
三、解答题(共8小题,满分70分)
-
16. 平面直角坐标系xOy中,点A在第一、三象限的角平分线上.点M(9,4).和点A在函数(x>0)的图象上.(1)、求k的值和点A的坐标;(2)、求直线AM对应的函数解析式.17. 如图①,四边形ABCD是正方形,点E是对角线AC上一点(点E不与点A,C重合),过点E作EF∥CD,交BC于点F,作EG∥BC,交CD于点G.
 (1)、求证:四边形EFGH是正方形;(2)、如图②,将四边形EFCG绕点C顺时针旋转α(0°<α<90°),连接AE,DG,求的值.18. 如图,热气球的探测器显示,从热气球所在位置A处看一栋楼顶部B处的仰角为35°,看这栋楼底部C处的俯角为61°.已知这栋楼BC的高度为400m,求热气球所在位置与该楼的水平距离(结果保留整数).(参考数据:tan35°≈0.70,tan61°≈1.80)
(1)、求证:四边形EFGH是正方形;(2)、如图②,将四边形EFCG绕点C顺时针旋转α(0°<α<90°),连接AE,DG,求的值.18. 如图,热气球的探测器显示,从热气球所在位置A处看一栋楼顶部B处的仰角为35°,看这栋楼底部C处的俯角为61°.已知这栋楼BC的高度为400m,求热气球所在位置与该楼的水平距离(结果保留整数).(参考数据:tan35°≈0.70,tan61°≈1.80) 19. 已知反比例函数的图象经过点A(-4,-2).(1)、求反比例函数表达式;(2)、若点在该函数图象上,求m的值.20. 如图,AD、AE分别是△ABC边BC上的高和中线,已知 , ∠C=45°.
19. 已知反比例函数的图象经过点A(-4,-2).(1)、求反比例函数表达式;(2)、若点在该函数图象上,求m的值.20. 如图,AD、AE分别是△ABC边BC上的高和中线,已知 , ∠C=45°. (1)、求AD的长;(2)、求sin∠BAE的值.21. 如图所示,延长平行四边形ABCD一边BC至点F,连结AF交CD于点E,若 .
(1)、求AD的长;(2)、求sin∠BAE的值.21. 如图所示,延长平行四边形ABCD一边BC至点F,连结AF交CD于点E,若 . (1)、若BC=3,求线段CF的长;(2)、若△ADE的面积为1,求平行四边形ABCD的面积.22. 挡车器是安全停车的好妿手,车轮与挡车器斜面相切为挡车有效状态.如图,某挡车器的横截面是等腰梯形ABCD,车轮⊙O与地面相切于点E,与挡车器斜面恰好相切于点A,点O,A,B,E再同一平面内.
(1)、若BC=3,求线段CF的长;(2)、若△ADE的面积为1,求平行四边形ABCD的面积.22. 挡车器是安全停车的好妿手,车轮与挡车器斜面相切为挡车有效状态.如图,某挡车器的横截面是等腰梯形ABCD,车轮⊙O与地面相切于点E,与挡车器斜面恰好相切于点A,点O,A,B,E再同一平面内. (1)、判断∠ABC与∠AOE的关系,并说明理由;(2)、测得挡车器腰长AB=10cm, , 求车轮⊙O的直径.23. 如图,AB为⊙O的直径,C为⊙O上一点,且点A,C不重合,P为⊙O外一点,PA=PC,连接AC,BC,连接OP交AC于点E,交⊙O于点D,连接DC.
(1)、判断∠ABC与∠AOE的关系,并说明理由;(2)、测得挡车器腰长AB=10cm, , 求车轮⊙O的直径.23. 如图,AB为⊙O的直径,C为⊙O上一点,且点A,C不重合,P为⊙O外一点,PA=PC,连接AC,BC,连接OP交AC于点E,交⊙O于点D,连接DC. (1)、当∠AOP=∠ACP时,求证:AP为⊙O的切线;(2)、在(1)的条件下,连接BP交CD于点F.当BC=6,tan∠ABP=时,求线段DF的长.
(1)、当∠AOP=∠ACP时,求证:AP为⊙O的切线;(2)、在(1)的条件下,连接BP交CD于点F.当BC=6,tan∠ABP=时,求线段DF的长.