湖北省黄冈市2023年中考三模数学试卷

试卷更新日期：2023-05-23 类型：中考模拟

进入出卷网下载

一、选择题（本大题共8小题，每小题3分，共24分）

1. -2的倒数是（）

A、2 B、-2 C、0 D、 $- \frac{1}{2}$

查看试题解析
2. 如图的三视图对应的物体是（）

A、 B、 C、 D、

查看试题解析
3. 中国信息通信研究院测算，2020-2025年，中国5G商用带动的信息消费规模将超过8万亿元，直接带动经济总产出达10.6万亿元．其中数据10.6万亿用科学记数法表示为（）

A、 $10.6 \times 1 0^{4}$ B、 $1.06 \times 1 0^{13}$ C、 $10.6 \times 1 0^{13}$ D、1.06 $\times 1 0^{8}$

查看试题解析
4. 下列计算正确的是（）

A、 ${(- 3 a b^{2})}^{2} = 6 a^{2} b^{4}$ B、 $- 6 a^{3} b \div 3 a b = - 2 a^{2} b$ C、 ${(a^{2})}^{3} - {(- a^{3})}^{2} = 0$ D、 ${(a + 1)}^{2} = a^{2} + 1$

查看试题解析
5. 如图，已知四边形ABCD是平行四边形，下列结论中不正确的是（）

A、当AB=BC时，它是菱形 B、当AC⊥BD时，它是菱形 C、当∠ABC=90°时，它是矩形 D、当AC=BD时，它是正方形

查看试题解析
6. 某校九年级有9名同学参加“建党一百周年”知识竞赛，预赛成绩各不相同，要取前5名参加决赛．小兰已经知道了自己的成绩，她想知道自己能否进入决赛，还需要知道这9名同学成绩的（）

A、中位数 B、众数 C、平均数 D、方差

查看试题解析
7. 如图，直线 $y = - \frac{\sqrt{3}}{3} x + 2$ 与x轴、y轴分别交于A、B两点，把 $△ A O B$ 绕点A顺时针旋转60°后得到 $△ A O^{'} B^{'}$ ，则点 $B^{'}$ 的坐标是（）

A、 $(4 ， 2 \sqrt{3})$ B、 $(2 \sqrt{3} ， 4)$ C、 $(\sqrt{3} ， 3)$ D、 $(2 \sqrt{3} + 2 ， 2 \sqrt{3})$

查看试题解析
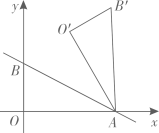8. 如图，正方形ABCD内接于 $⊙ O$ ，线段MV在对角线BD上运动，若 $⊙ O$ 的面积为2π， $M N = 1$ ，则 $△ A M N$ 周长的最小值是（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题（本大题共8小题，每小题3分，共24分）

9. 要使根式 $\sqrt{a - 5}$ 有意义，则a的取值范围是．

查看试题解析
10. 如图， $A B ∥ C D$ ，点E在BC上， $C D = C E$ ．若 $∠ A B C = 34 °$ ，则 $∠ B E D$ 的度数是．

查看试题解析
11. 如图，⊙ $O$ 的半径为2，点A，B，C都在⊙ $O$ 上，若 $∠ B = 30 °$ .则 $\overset{⌢}{A C}$ 的长为（结果用含有 $π$ 的式子表示）

查看试题解析
12. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C < B C$ ．分别以点A，B为圆心，大于 $\frac{1}{2} A B$ 的长为径画弧，两弧交于D，E两点，直线DE交BC于点F，连接AF．以点A为圆心，AF为半径弧，交BC延长线于点H，连接AH．若 $B C = 3$ ，则 $△ A F H$ 的周长为．

查看试题解析
13. 对于实数 $a ， b$ ，定义运算“◎”如下： $a$ ◎ $b$ $= {(a + b)}^{2} - {(a - b)}^{2}$ .若 $(m + 2)$ ◎ $(m - 3)$ $= 24$ ，则 $m =$ .

查看试题解析
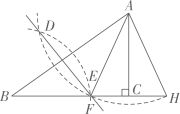14. 如图，无人机于空中A处测得某建筑顶部B处的仰角为45°，测得该建筑底部C处的为35°．若无人机的飞行高度AD为42 m，则该建筑的高度BC为m．（参考数据： $s i n 35 ° \approx 0.57$ ， $c o s 35 ° \approx 0.82$ ， $t a n 35 ° \approx 0.70$ ）．

查看试题解析

15. 古希腊数学家定义了五边形数，如下表所示，将点按照表中方式排列成五边形点阵，表中的点的个数即五边形数；

图形	•						…
五边形擞	1	5	12	22	35	51	…

将五边形数1，5，12，22，35，51，…，排成如下数表；

观察这个数表，则这个数表中的第八行从左至右第2个数为．

查看试题解析

16. 已知抛物线 $y = a x^{2} + b x + c$ （a，b，c是常数）开口向下，过 $A (- 1 ， 0)$ ， $B (m ， 0)$ 且 $1 < m < 2$ ．下列四个结论：
① $b > 0$ ；②若 $m = \frac{3}{2}$ ，则 $3 a + 2 c < 0$ ；

③若点 $M (x_{1} ， y_{1})$ ， $N (x_{2} ， y_{2})$ 在抛物线上， $x_{1} < x_{2}$ ，且 $x_{1} + x_{2} > 1$ ，则 $y_{1} > y_{2}$ ；

④当 $a \leq - 1$ 时，关于x的一元二次方程 $a x^{2} + b x + c = 1$ 必有两个不相等的实数根．其中正确的是（填写序号）．

查看试题解析

三、解答题（本大题共8小题，共72分）

17. 计算； ${(\frac{1}{2})}^{- 1} + {(π - 3)}^{0} - 2 \cos 30 ° + | 3 - \sqrt{12} |$

查看试题解析
18. 某校决定购买A，B两种奖品，用于表彰在“消防知识竞赛”活动中表现突出的学生．已知A奖品比B奖品每件多25元，预算资金为1700元，其中800元购买A奖品，其余资金购买B奖品，且购买B奖品的数量是A奖品的3倍．

(1)、求A，B奖品的单价；

(2)、购买当日，正逢该店搞促销活动，所有商品均按原价八折销售，故学校调整了购买方案：不超过预算资金且购买A奖品的资金不少于720元，A，B两种奖品共100件，求购买A，B两种奖品的数量，有哪几种方案？

查看试题解析
19. 某校为了解九年级学生体质健康情况，随机抽取了部分学生进行体能测试，并根据测试结果绘制了不完整的条形统计图和扇形统计图，请回答下列问题．

(1)、在这次调查中，“优秀”所在扇形的圆心角的度数是；

(2)、请补全条形统计图；

(3)、若该校九年级共有学生1200人，则估计该校“良好”的人数是；

(4)、已知“不及格”的3名学生中有2名男生、1名女生，如果从中随机抽取两名同学进行体能加试，请用列表法或画树状图的方法，求抽到两名男生的概率是多少？

查看试题解析
20. 如图，AB、AC分别是 $⊙ O$ 的直径和弦，点D为劣弧 $\overset{⌢}{A C}$ 上一点，弦ED交AB于点H，交AC于点F，过点C的切线交ED的延长线于点P．

(1)、若 $P C = P F$ ，求证： $A B ⊥ E D$ ；

(2)、试探究：当点D在劣弧 $\overset{⌢}{A C}$ 的什么位置时使得 $A D^{2} = D E \cdot D F$ ，请说明理由．

查看试题解析
21. 如图，一次函数 $y = - \frac{1}{2} x + \frac{5}{2}$ 的图象与反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象交于A，B两点，过点A作x轴的垂线，垂足为M， $△ A O M$ 面积为1．

(1)、求反比例函数的解析式；

(2)、在x轴上求一点P，使 $| P A - P B |$ 的值最大，并求出其最大值和P点坐标．

查看试题解析
22. 为了振兴乡村经济，我市某镇鼓励广大农户种植山药，并精加工成甲、乙两种产品、某经销商购进甲、乙两种产品，甲种产品进价为8元/kg；乙种产品的进货总金额y（单位：元）与乙种产品进货量x（单位：kg）之间的关系如图所示．已知甲、乙两种产品的售价分别为12元/kg和18元/kg．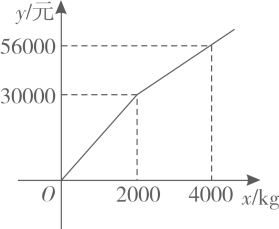

(1)、求出 $0 \leq x \leq 2000$ 和 $x > 2000$ 时，y与x之间的函数关系式；

(2)、若该经销商购进甲、乙两种产品共6000 kg，并能全部售出．其中乙种产品的进货量不低于1600 kg，且不高于4000 kg，设销售完甲、乙两种产品所获总利润为w元（利润=销售额-成本），
请求出w（单位：元）与乙种产品进货量x（单位：kg）之间的函数关系式，并为该经销商设计出获得最大利润的进货方案；

(3)、为回馈广大客户，该经销商决定对两种产品进行让利销售．在（2）中获得最大利润的进货方案下，甲、乙两种产品售价分别降低a元/kg和2a元/kg，全部售出后所获总利润不低于15000元，求a的最大值．

查看试题解析
23. 如图1，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ， $∠ A C B = 60 °$ ， $A C = 2$ ，点 $A_{1}$ ， $B_{1}$ 为边AC，BC的中点，连接 $A_{1} B_{1}$ ，将 $△ A_{1} B_{1} C$ 绕点C逆时针旋转 $α (0 ° \leq α \leq 360 °)$ ．

(1)、如图1，当 $α = 0 °$ 时， $\frac{B B_{1}}{A A_{1}} =$ ， $B B_{1}$ ， $A A_{1}$ 所在直线相交所成的较小夹角的度数为；

(2)、将 $△ A_{1} B_{1} C$ 绕点C逆时针旋转至图2所示位置时，（1）中结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；

(3)、在 $△ A_{1} B_{1} C$ 绕点C逆时针旋转过程中，
① $S_{△ A B A_{1}}$ 的最大值为 ▲ ；

②当 $A_{1}$ ， $B_{1}$ ， B三点共线时，请求出线段 $B B_{1}$ 的长.

查看试题解析
24. 如图1，抛物线 $y = \frac{\sqrt{2}}{4} x^{2} + b x + c$ 与x轴交于A、B两点，点A、B分别位于原点左、右两侧，且 $A O = 2 B O = 4$ ，过A点的直线 $y = k x + c$ 交y轴于点C．

(1)、求k、b、c的值；

(2)、在抛物线的对称轴上是否存在一点P，使 $△ A C P$ 为直角三角形？若存在，请直接写出所有满足条件的点的坐标；若不存在，请说明理由；

(3)、如图2，点M为线段AC上一点，连接OM，求 $\frac{1}{2} A M + O M$ 的最小值．

查看试题解析