湖北省黄冈市、孝感市、咸宁市2023年中考模拟数学试题（4月）

试卷更新日期：2023-05-23 类型：月考试卷

进入出卷网下载

一、精心选一选（本大题共8小题，每小题3分，满分24分．）

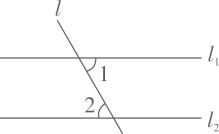
1. 23的相反数为（）

A、-23 B、32 C、-32 D、 $\pm 23$

查看试题解析
2. 中国空间站“天宫一号”运行在距离地球平均高度约375000米处，数375000用科学记数法表示为（）

A、 $375 \times 1 0^{3}$ B、 $37.5 \times 1 0^{4}$ C、 $3.75 \times 1 0^{5}$ D、 $0.375 \times 1 0^{6}$

查看试题解析
3. 如图，直线 $l_{1} ∥ l_{2}$ ，直线l与 $l_{1}$ ， $l_{2}$ 相交，若图中∠1=60°，则∠2=（）

A、55° B、60° C、65° D、70°

查看试题解析
4. 如图是某几何体的三视图，该几何体是（）

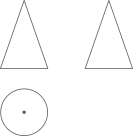A、圆柱 B、正方体 C、三棱柱 D、圆锥

查看试题解析
5. 平面直角坐标系中，若点 $A (- 1 ， a)$ 与点 $B (b ， 3)$ 关于x轴对称，则点 $C (a ， b)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 如图， $△ A B C$ 是 $⊙ O$ 的内接三角形，AC是 $⊙ O$ 的直径，∠C=50°，∠ABC的平分线BD交 $⊙ O$ 于点D，则∠BAD=（）

A、80° B、85° C、90° D、95°

查看试题解析
7. 如图， $R t △ A B C$ 中，∠B=90°，以C为圆心适当长为半径画弧，分别交AC，BC于点E，F，再分别以点E，F为圆心，大于 $\frac{1}{2} E F$ 的长为半径画弧交于点P，作射线CP交AB于点D，已知BD=3，AC=8，则 $△ A C D$ 的面积为（）

A、12 B、24 C、16 D、8

查看试题解析
8. 已知抛物线 $y = a x^{2} + b x + c (a > 0)$ 的对称轴为直线x=-1，与x轴的一个交点为 $A (m ， 0)$ ， 0<m<1，下列结论中：①abc>0；②4a+c>0；③若t为任意实数，则有 $a - b t \leq a t^{2} + b$ ；④当此抛物线经过点 $(\frac{1}{2} ， 2)$ 时，方程 $a x^{2} + b x + c - 2 = 0$ 的两根为 $x_{1} ， x_{2} (x_{1} < x_{2})$ ，可求得 $x_{1} + 2 x_{2} = - 2$ ，正确结论的序号为（）

A、①②③ B、②③ C、③④ D、②③④

查看试题解析

二、细心填一填（本大题共8小题，每小题3分，满分24分．）

9. 计算： $| - 3 | - {(\frac{1}{2})}^{0} =$ ．

查看试题解析
10. 试写出一个x值使得二次根式 $\sqrt{x - 4}$ 有意义：x= ．

查看试题解析

11. 为了促进“双减”政策有效落实，市教育局对启智中学八年级学生的课外作业时长进行了问卷调查，50名学生的作业时长统计如下表，这组作业时长数据中，中位数是．

作业时长（单位：分钟）	50	60	70	80
人数（单位：人）	14	11	10	15

查看试题解析

12. 已知 $x_{1}$ ， $x_{2}$ 是一元二次方程 $x^{2} - 2 x - 5 = 0$ 的两个实数根，则 $x_{1} + x_{2} + 3 x_{1} x_{2} =$ ．

查看试题解析
13. 如图，正方形ABCD的对角线交于点O， $A B = 2 \sqrt{2}$ ，现有半径足够大的扇形OEF，∠EOF=90°，当扇形OEF绕点O转动时，扇形OEF和正方形ABCD重叠部分的面积为．

查看试题解析
14. 如图是矗立在高速公路边水平地面上的交通警示牌，经过测量得到如下数据： $A M = 4$ 米， $A B = 8$ 米， $∠ M A D = 45 °$ ， $∠ M B C = 30 °$ ，则 $C D$ 的长为米.（结果保留根号）

查看试题解析
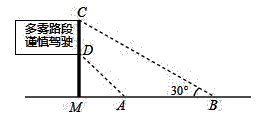15. 我国南宋著名数学家杨辉精研数学，著有《详解九章算法》，对数的运算进行了深入研究与总结．类比其中的思想方法，可以解决很多数与式的计算问题．现已知a，b为实数，且a+b=3，ab=1，计算可得： $a^{2} + b^{2} = 7$ ， $a^{3} + b^{3} = 18$ ， $a ⁴ + b^{4} = 47$ ， …，由此求得 $a^{5} + b^{5} =$ ．

查看试题解析
16. 已知平面直角坐标系中两定点 $C (0 ， 4)$ ， $K (6 ， 0)$ ， A为线段OK上一动点，连接AC，取AC中点为D，将线段AD绕点A顺时针旋转90°得到AB，连接BK，当BK取最小值时，B点坐标为．

查看试题解析

三、专心解一解（本大题共8小题，满分72分．）

17. 化简 $\frac{x + 4}{x^{2} + 3 x} - \frac{1}{3 x + x^{2}}$ ．

查看试题解析
18. “巩固脱贫攻坚成果，拓展乡村振兴教育赛道”，某农民企业家计划为崇礼中学购买甲、乙两种词典．已知购买1本甲种词典和2本乙种词典共需170元，购买2本甲种词典和3本乙种词典共需290元．

(1)、求每本甲种词典和每本乙种词典的价格分别为多少元？

(2)、该企业家计划购买甲种词典和乙种词典共300本，总费用不超过16000元，那么最多可购买甲种词典多少本？

查看试题解析
19. 学生在体育锻炼中能享受乐趣，增强体质，健全人格，锤炼意志．尚美中学开展了“一人一球”的体育选考活动，学生根据自己的特长选择一门球类项目（A：篮球，B：足球，C：排球，D：羽毛球，E：乒乓球），刘老师组织数学兴趣小组随机对该校部分学生的选考情况进行调查，根据收集到的数据制成了两幅不完整的统计图（如图所示）：

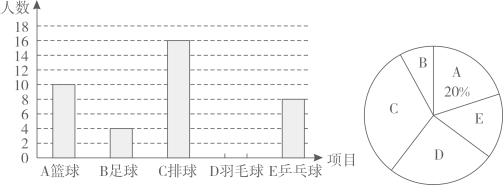(1)、兴趣小组调查的学生人数是 ▲ 人，请将条形统计图补充完整；

(2)、扇形统计图中A类所对应的扇形圆心角大小为；

(3)、现有4名学生，2人选篮球，1人选足球，1人选排球，兴趣小组要从这4人中任选2人了解他们对体育选考的看法，请用列表或圆树状图的方法求出所选2人都选篮球的概率．

查看试题解析
20. 如图，直线AF与 $⊙ O$ 相切于点A，弦 $B C ∥ A F$ ，连接BO并延长交 $⊙ O$ 于点E，连接CE并延长交AF于点D．

(1)、求证： $C E ∥ O A$ ；

(2)、若 $⊙ O$ 的半径r=10，BC=16，求DE的长．

查看试题解析
21. 如图，一次函数 $y = k_{1} x + b$ 与反比例函数 $y = \frac{k_{2}}{x}$ 的图象相交于A，B两点，其中点A的坐标为 $(- 2 ， 3)$ ，点B的横坐标为6．

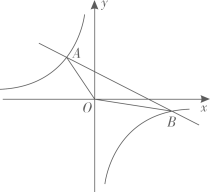(1)、求这两个函数的解析式；

(2)、根据图象，直接写出满足 $k_{1} x + b - \frac{k_{2}}{x} > 0$ 的x的取值范围；

(3)、连接OA，OB，点P在直线AB上， $S_{△ A O P} = \frac{1}{4} S_{△ B O P}$ ，请直接写出满足题意的P点坐标．

查看试题解析
22. 某经销商到“幸福村”蔬菜种植基地定点采购甲种蔬菜，已知甲种蔬菜的单价y（元/千克）与采购量x（千克）之间的函数关系如图中折线AB-BC-CD所示（不包括端点A）．

(1)、当100<x<200时，直接写出y与x之间的函数解析式；

(2)、若甲种蔬菜的种植成本为4元/千克，采购量不超过200千克，那么当采购量是多少时，蔬菜种植基地获利最大，最大利润是多少元？

(3)、在（2）的条件下，求采购甲种蔬菜多少千克时，蔬菜种植基地能获利418元？

查看试题解析
23. 如图， $△ A B C$ 和 $△ D E F$ 是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，点E为线段BC上一点，将 $△ D E F$ 绕点E旋转时，线段DE与AB交于点P，线段EF与直线CA交于点Q．

(1)、如图①，点Q在线段AC上且BP=CE时，求证： $△ B P E ≌ △ C E Q$ ；

(2)、如图②，点Q在线段CA的延长线上时，求证： $△ B P E ∽ △ C E Q$ ；

(3)、如图③，点Q在线段CA的延长线上，若 $\frac{B E}{B C} = \frac{1}{3}$ ， $B P = \frac{2}{3} a$ ， $C Q = \frac{8}{3} a$ ，求P，Q两点间的距离．（用含a的代数式表示）

查看试题解析
24. 如图，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与x轴交于 $A (- 3 ， 0)$ ， $B (1 ， 0)$ 两点，与y轴负半轴交于点C，且OC=4OB，点P是直线AC下方抛物线上一动点．

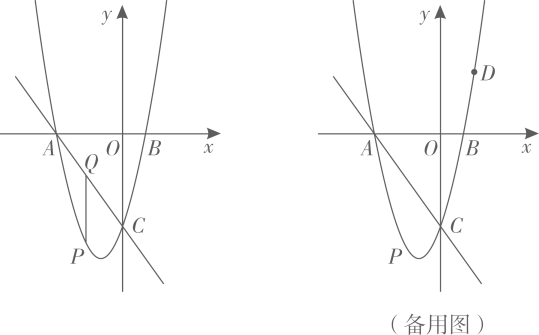(1)、请直接写出 $a =$ ， $b =$ ， $c =$ ， $c o s ∠ B A C =$ ；

(2)、过点P作 $P Q ∥ y$ 轴交直线AC于点Q，求 $P Q + \frac{3}{5} A Q$ 的最大值及此时P点的坐标；

(3)、若点P横坐标为 $- \frac{3}{2}$ ， D为第一象限内抛物线上一点，连接PD交AC于点M，当 $△ A D M$ 与 $△ A P M$ 面积之比为 $\frac{40}{9}$ 时，求点M的坐标．

查看试题解析