四川省自贡市2023年中考一模数学试题
试卷更新日期:2023-05-23 类型:中考模拟
一、单选题
-
1. 如图 与 不是对顶角的是( )A、
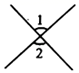 B、
B、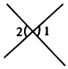 C、
C、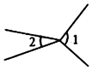 D、
D、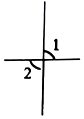 2. 据统计,截至北京时间2020年11月25日,全球累计确诊新冠肺炎病例已经起过60040000例,数据60040000用科学记数法可表示为( )A、 B、 C、 D、3. 下面四个立体图形中,和其他三个立体图形不同类的是( )A、
2. 据统计,截至北京时间2020年11月25日,全球累计确诊新冠肺炎病例已经起过60040000例,数据60040000用科学记数法可表示为( )A、 B、 C、 D、3. 下面四个立体图形中,和其他三个立体图形不同类的是( )A、 B、
B、 C、
C、 D、
D、 4. 下列运算中,正确的是( )A、(ab2)2=a2b4 B、a2+a2=2a4 C、a2•a3=a6 D、a6÷a3=a25. 菱形的周长为8cm,高为1cm,则该菱形两邻角度数比为()A、3:1 B、4:1 C、5:1 D、6:16. 下列图形是化学中常用实验仪器的平面示意图,从左至右分别代表广口瓶、圆底瓶、蒸馏烧瓶和锥形瓶,其中不是轴对称图形的是( )A、
4. 下列运算中,正确的是( )A、(ab2)2=a2b4 B、a2+a2=2a4 C、a2•a3=a6 D、a6÷a3=a25. 菱形的周长为8cm,高为1cm,则该菱形两邻角度数比为()A、3:1 B、4:1 C、5:1 D、6:16. 下列图形是化学中常用实验仪器的平面示意图,从左至右分别代表广口瓶、圆底瓶、蒸馏烧瓶和锥形瓶,其中不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 如图,是的外接圆,是的直径, , 则的度数是( )
7. 如图,是的外接圆,是的直径, , 则的度数是( )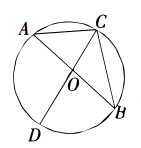 A、 B、 C、 D、8. 两组数据如下图,设图(1)中数据的平均数为、方差为 , 图(2)中数据的平均数为、方差为 , 则下列关系成立的是( ).
A、 B、 C、 D、8. 两组数据如下图,设图(1)中数据的平均数为、方差为 , 图(2)中数据的平均数为、方差为 , 则下列关系成立的是( ).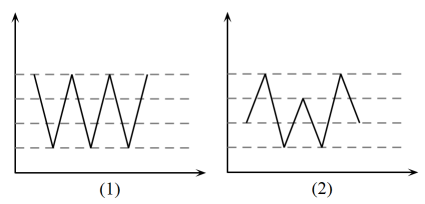 A、 B、 C、 D、9. 等腰三角形的一个内角是50°,则其底角是( )A、65°或50° B、65° C、50° D、65°或80°10. 如图,、切于点A、B,点C是上一点,且 , 则为( )
A、 B、 C、 D、9. 等腰三角形的一个内角是50°,则其底角是( )A、65°或50° B、65° C、50° D、65°或80°10. 如图,、切于点A、B,点C是上一点,且 , 则为( ) A、 B、 C、 D、11. 在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )A、 B、 C、 D、12. 二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点横坐标为﹣2,x0 , 且满足(a+b+c)(4a+2b+c)<0,与y轴的负半轴相交,抛物线经过点A(﹣1,y1),B(﹣ ,y2),C(1,y3),正确结论是( )A、y3>y2>y1 B、y3>y1>y2 C、y1>y2>y3 D、y1>y3>y2
A、 B、 C、 D、11. 在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )A、 B、 C、 D、12. 二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点横坐标为﹣2,x0 , 且满足(a+b+c)(4a+2b+c)<0,与y轴的负半轴相交,抛物线经过点A(﹣1,y1),B(﹣ ,y2),C(1,y3),正确结论是( )A、y3>y2>y1 B、y3>y1>y2 C、y1>y2>y3 D、y1>y3>y2二、填空题
-
13. 绝对值小于4的所有负整数的和是 .14. 多项式 的公因式是.15. 若 , 则= .16. 如图,某校根据学生上学方式的一次抽样调查结果,绘制出一个未完成的扇形统计图,若该校共有学生700人,则据此估计步行的有人.
 17. 如图,点P是等边△ABC内的一点,PA=6,PB=8,PC=10,若点P′是△ABC外的一点,且△P′AB≌△PAC,则∠APB的度数为.
17. 如图,点P是等边△ABC内的一点,PA=6,PB=8,PC=10,若点P′是△ABC外的一点,且△P′AB≌△PAC,则∠APB的度数为. 18. 如图,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2.若直线l经过点E,将该菱形的面积平分,并与菱形的另一边交于点F,则线段EF的长为.
18. 如图,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2.若直线l经过点E,将该菱形的面积平分,并与菱形的另一边交于点F,则线段EF的长为.
三、解答题
-
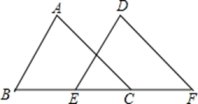
19. 解不等式组: ,并把解集在数轴上表示出来.20. 如图,在△ABC与△DEF中,如果AB=DE,BE=CF,∠ABC=∠DEF;求证:AC∥DF.
 21. 为了防止雾霾,某口罩生产企业需要在若干天内加工2400个口罩,在实际生产中,由于提高了生产技术水平,每天加工的个数为原来的1.5倍,从而提前2天完成任务,问该企业原计划每天生产多少个口罩?22. 2021年,“碳中和、碳达峰”成为高频热词.为了解学生对“碳中和、碳达峰”知识的知晓情况,某校团委随机对该校九年级部分学生进行了问卷调查,调查结果共分成四个类别:A表示“从未听说过”,B表示“不太了解”,C表示“比较了解”,D表示“非常了解”.根据调查统计结果,绘制成两种不完整的统计图.请结合统计图,回答下列问题.
21. 为了防止雾霾,某口罩生产企业需要在若干天内加工2400个口罩,在实际生产中,由于提高了生产技术水平,每天加工的个数为原来的1.5倍,从而提前2天完成任务,问该企业原计划每天生产多少个口罩?22. 2021年,“碳中和、碳达峰”成为高频热词.为了解学生对“碳中和、碳达峰”知识的知晓情况,某校团委随机对该校九年级部分学生进行了问卷调查,调查结果共分成四个类别:A表示“从未听说过”,B表示“不太了解”,C表示“比较了解”,D表示“非常了解”.根据调查统计结果,绘制成两种不完整的统计图.请结合统计图,回答下列问题.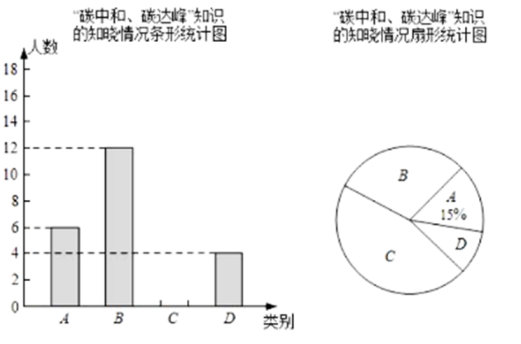 (1)、参加这次调查的学生总人数为人;(2)、扇形统计图中,B部分扇形所对应的圆心角是;(3)、将条形统计图补充完整;(4)、在D类的学生中,有2名男生和2名女生,现需从这4名学生中随机抽取2名“碳中和、碳达峰”知识的义务宣讲员,请利用画树状图或列表的方法,求所抽取的2名学生恰好是1名男生和1名女生的概率.23. 已知双曲线与直线相交于A(-3,m)、B两点.(1)、直接写出此双曲线的解析式;(2)、若点M(a,b),且a,b都是不大于3的正整数,用画树状图法或列表法求点M在双曲线上的概率.24. 如图,在等腰中, , 以为直径作 , 交于点D,过点D作 , 垂足为E.
(1)、参加这次调查的学生总人数为人;(2)、扇形统计图中,B部分扇形所对应的圆心角是;(3)、将条形统计图补充完整;(4)、在D类的学生中,有2名男生和2名女生,现需从这4名学生中随机抽取2名“碳中和、碳达峰”知识的义务宣讲员,请利用画树状图或列表的方法,求所抽取的2名学生恰好是1名男生和1名女生的概率.23. 已知双曲线与直线相交于A(-3,m)、B两点.(1)、直接写出此双曲线的解析式;(2)、若点M(a,b),且a,b都是不大于3的正整数,用画树状图法或列表法求点M在双曲线上的概率.24. 如图,在等腰中, , 以为直径作 , 交于点D,过点D作 , 垂足为E.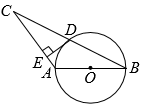 (1)、求证:是的切线;(2)、如果 , , 求的长.25. 为为加强对市内道路交通安全的监督,王警官利用无人机进行检测.某高架路有一段限速每小时60千米的道路AB(如图所示),当无人机在限速道路的正上方C处时,测得限速道路的起点A的俯角是37°,无人机继续向右水平飞行220米到达D处,此时又测得起点A的俯角是30°,同时测得限速道路终点B的俯角是45°(注:即四边形ABDC是梯形).
(1)、求证:是的切线;(2)、如果 , , 求的长.25. 为为加强对市内道路交通安全的监督,王警官利用无人机进行检测.某高架路有一段限速每小时60千米的道路AB(如图所示),当无人机在限速道路的正上方C处时,测得限速道路的起点A的俯角是37°,无人机继续向右水平飞行220米到达D处,此时又测得起点A的俯角是30°,同时测得限速道路终点B的俯角是45°(注:即四边形ABDC是梯形).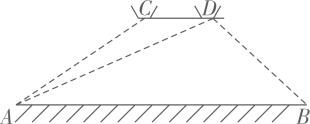 (1)、求限速道路AB的长(精确到1米);(2)、如果李师傅在道路AB上行驶的时间是1分20秒,请判断他是否超速?并说明理由.
(1)、求限速道路AB的长(精确到1米);(2)、如果李师傅在道路AB上行驶的时间是1分20秒,请判断他是否超速?并说明理由.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,)
26. 综合与探究如图,已知抛物线经过 , 两点,交y轴于点C.
 (1)、求抛物线的解析式,连接 , 并求出直线的解析式;(2)、请在抛物线的对称轴上找一点P,使的值最小,此时点P的坐标是(3)、点Q在第一象限的抛物线上,连接CQ,BQ,求出△BCQ面积的最大值.(4)、点M为x轴上一动点,在抛物线上是否存在一点N,使得以A、C、M、N四点为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式,连接 , 并求出直线的解析式;(2)、请在抛物线的对称轴上找一点P,使的值最小,此时点P的坐标是(3)、点Q在第一象限的抛物线上,连接CQ,BQ,求出△BCQ面积的最大值.(4)、点M为x轴上一动点,在抛物线上是否存在一点N,使得以A、C、M、N四点为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.