四川省资阳市安岳县2023年中考一模数学试题
试卷更新日期:2023-05-23 类型:中考模拟
一、单选题
-
1. 3的相反数是( )A、3 B、 C、 D、-32. 下列运算正确的是( )A、 B、 C、 D、3. 将两本相同的书进行叠放,得到如图所示的几何体,则它的正视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 2008年5月,汶川大地震,土耳其向我国捐赠人民币约1400万元.2023年2月,土耳其工地震,我国首批援助土耳其人民币4000万元,可谓是“滴水之恩,当涌泉相报”!请将“4000万”用科学记数法表示为( )A、 B、 C、 D、5. 如图, , , , 则的度数为( )
4. 2008年5月,汶川大地震,土耳其向我国捐赠人民币约1400万元.2023年2月,土耳其工地震,我国首批援助土耳其人民币4000万元,可谓是“滴水之恩,当涌泉相报”!请将“4000万”用科学记数法表示为( )A、 B、 C、 D、5. 如图, , , , 则的度数为( ) A、 B、 C、 D、6. 《义务教育课程标准(年版)》首次把学生学会炒菜纳入劳动教育课程,并做出明确规定.某班有名学生已经学会炒的菜品的种数依次为: , 则这组数据的众数和中位数分别是( )A、 B、 C、 D、7. 设n为整数,且 , 则n的值为( )A、3 B、4 C、5 D、68. 如图,在正方形中,对角线的长为 , 以点A为圆心,长为半径画弧交于点E,则图中阴影部分的面积为( )
A、 B、 C、 D、6. 《义务教育课程标准(年版)》首次把学生学会炒菜纳入劳动教育课程,并做出明确规定.某班有名学生已经学会炒的菜品的种数依次为: , 则这组数据的众数和中位数分别是( )A、 B、 C、 D、7. 设n为整数,且 , 则n的值为( )A、3 B、4 C、5 D、68. 如图,在正方形中,对角线的长为 , 以点A为圆心,长为半径画弧交于点E,则图中阴影部分的面积为( )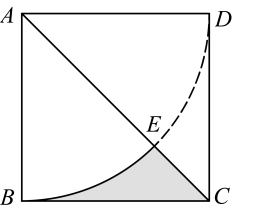 A、 B、 C、 D、9. 已知二次函数 , 当时,y的最小值为( )A、 B、 C、 D、710. 如图,在矩形中, , 点分别在边上,且 , , 将矩形沿折叠后,点分别落在处,延长交于点G.当三点共线时,的长为( )
A、 B、 C、 D、9. 已知二次函数 , 当时,y的最小值为( )A、 B、 C、 D、710. 如图,在矩形中, , 点分别在边上,且 , , 将矩形沿折叠后,点分别落在处,延长交于点G.当三点共线时,的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 陈老师准备在班内开展“道德”、“心理”、“安全”三场专题教育讲座,若三场讲座随机安排,则“心理”专题讲座被安排在第一场的概率为 .12. 若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是 .13. 已知a+b=2,ab=1,则a2 + b2= .
14. 如图,是的直径,C为延长线上一点,切于点D.若 , , 则的长为 .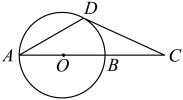 15. 如图,A、B是坐标轴上两点,反比例函数的图像经过的中点C,若 , 则k的值为 .
15. 如图,A、B是坐标轴上两点,反比例函数的图像经过的中点C,若 , 则k的值为 . 16. 已知矩形按如图方式放置,且 , 将矩形OABC绕点C顺时针旋转至矩形处时,为第一次旋转;将矩形绕点顺时针旋转至矩形处时,为第二次旋转;将矩形绕点顺时针旋转至矩形处时,为第三次旋转;…,按此规律,旋转2023次后,所得矩形中右上角顶点的坐标为 .
16. 已知矩形按如图方式放置,且 , 将矩形OABC绕点C顺时针旋转至矩形处时,为第一次旋转;将矩形绕点顺时针旋转至矩形处时,为第二次旋转;将矩形绕点顺时针旋转至矩形处时,为第三次旋转;…,按此规律,旋转2023次后,所得矩形中右上角顶点的坐标为 .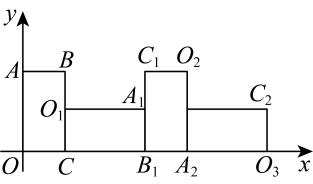
三、解答题
-
17. 先化简,再求值: , 其中 .18. 安岳石窟以其历史悠久,规模庞大,题材丰富,技艺精湛而闻名,素有“中国佛雕之都”的美誉!2023年春节期间,小月同学就游客对其中的四处景点(A.圆觉洞;B.毗卢洞;C.卧佛院;D.千佛寨),作为最佳旅游景点的情况进行了抽样调查,并将调查结果绘制成如图8所示的两幅不完整的统计图.

请你根据统计图中所提供的信息解答下列问题:
(1)、请求出m的值并补全条形统计图;(2)、若某批次游客有2000人,请估计选择C景点作为最佳旅游景点的游客人数;(3)、已知把D景点作为最佳旅游景点的游客中有3名女士和2名男士,若从中随机抽取2人进行深入了解,请用画树状图或列表法求出恰好抽到1名男士和1名女士的概率.19. 我县初三实考在即,为了更好地备考,某校准备提前采购A、B两类实验器材.经查询,若购买A类实验器材2套和B类实验器材1套共需1000元;若购买A类实验器材2套和B类实验器材3套共需1800元.(1)、分别求出A、B两类实验器材每套的价格;(2)、经核算,该校决定共购买这两类实验器材30套,其中A类实验器材的数量不多于B类实验器材数量的2倍.如何购买才能使总费用最低?最低费用是多少元?20. 如图,已知一次函数与反比例函数的图象交于、两点,与x轴交于C点. (1)、求一次函数的解析式;(2)、若点C关于y轴的对称点为D点,连结、 , 求的面积.21. 如图,在中,O为的中点,过点O作交于点E,交于点F.
(1)、求一次函数的解析式;(2)、若点C关于y轴的对称点为D点,连结、 , 求的面积.21. 如图,在中,O为的中点,过点O作交于点E,交于点F.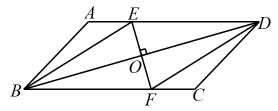 (1)、求证:四边形是菱形;(2)、若 , 求的长.22. 如图是一景区观光台侧面示意图,直达观光台顶A的斜梯长为15米,其坡度 . 由于游客量的增加,此斜梯存在一定的安全隐患,当地政府决定对其改建,在与B处同一水平面的C处起修建斜梯和缓冲平台 , 其中米,米,且在A处看E处的俯角为 , 在C处看D处的仰角为 .
(1)、求证:四边形是菱形;(2)、若 , 求的长.22. 如图是一景区观光台侧面示意图,直达观光台顶A的斜梯长为15米,其坡度 . 由于游客量的增加,此斜梯存在一定的安全隐患,当地政府决定对其改建,在与B处同一水平面的C处起修建斜梯和缓冲平台 , 其中米,米,且在A处看E处的俯角为 , 在C处看D处的仰角为 . (1)、求观光台顶A到地面的距离;(2)、求B、C两处的距离.
(1)、求观光台顶A到地面的距离;(2)、求B、C两处的距离.