四川省宜宾市柳嘉镇2023年中考一模数学试题
试卷更新日期:2023-05-23 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、21 C、 D、2. 某市轨道交通沿线站点为33个,全长37200米.将37200用科学记数法表示为( )A、 B、 C、 D、3. 下列几何体的三种视图都是圆形的是( )A、
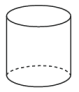 B、
B、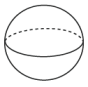 C、
C、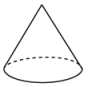 D、
D、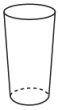 4. 下列计算正确的是( )A、 B、 C、 D、5. 关于x的不等式的解集如图所示,则a的值是( )
4. 下列计算正确的是( )A、 B、 C、 D、5. 关于x的不等式的解集如图所示,则a的值是( ) A、0 B、2 C、 D、6. 如图所示,是我县2018年9月某周内最高气温的折线统计图,关于这7天的日最高气温的数据中,众数和中位数分别是( )
A、0 B、2 C、 D、6. 如图所示,是我县2018年9月某周内最高气温的折线统计图,关于这7天的日最高气温的数据中,众数和中位数分别是( ) A、28,24 B、28,26 C、28,28 D、30,267. 如图, 的度数可能是( )
A、28,24 B、28,26 C、28,28 D、30,267. 如图, 的度数可能是( ) A、50° B、60° C、70° D、120°8. 某市为解决冬季取暖问题需铺设一条长米的管道,为尽量减少施工对交通造成的影响,实际施工时“…”,设实际每天铺设管道x米,则可得方程 , 根据此情景,题中用“…”表示的缺失的条件应补为( )A、每天比原计划多铺设米,结果提前天先成 B、每天比原计划少铺设米,结果延期天完成 C、每天比原计划少铺设米,结果延期天完成 D、每天比原计划多铺设米,结果提前天完成9. 如图,过圆外一点P作⊙O的两条切线,切点分别为A、B , 连接AB , 在AB、PB、PA上分别取一点D、E、F , 使AD=BE , BD=AF , 连接DE、DF、EF , 则∠EDF等于( )
A、50° B、60° C、70° D、120°8. 某市为解决冬季取暖问题需铺设一条长米的管道,为尽量减少施工对交通造成的影响,实际施工时“…”,设实际每天铺设管道x米,则可得方程 , 根据此情景,题中用“…”表示的缺失的条件应补为( )A、每天比原计划多铺设米,结果提前天先成 B、每天比原计划少铺设米,结果延期天完成 C、每天比原计划少铺设米,结果延期天完成 D、每天比原计划多铺设米,结果提前天完成9. 如图,过圆外一点P作⊙O的两条切线,切点分别为A、B , 连接AB , 在AB、PB、PA上分别取一点D、E、F , 使AD=BE , BD=AF , 连接DE、DF、EF , 则∠EDF等于( ) A、90°﹣∠P B、90°﹣ ∠P C、180°﹣∠P D、45°﹣ ∠P10. 八(1)班同学参加社会实践活动,在王伯伯的指导下,要围一个如图所示的长方形菜园 , 菜园的一边利用足够长的墙,用篱笆围成的另外三边的总长恰好为12m,设边的长为xm,边的长为ym . 则y与x之间的函数表达式为( )
A、90°﹣∠P B、90°﹣ ∠P C、180°﹣∠P D、45°﹣ ∠P10. 八(1)班同学参加社会实践活动,在王伯伯的指导下,要围一个如图所示的长方形菜园 , 菜园的一边利用足够长的墙,用篱笆围成的另外三边的总长恰好为12m,设边的长为xm,边的长为ym . 则y与x之间的函数表达式为( ) A、 B、 C、 D、11. 已知二次函数 ( 为常数, )当 时, ,则该函数图象的顶点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限12. 如图,是等边三角形,点D,E分别在 , 上,且 , , 与相交于点F,则下列结论:① , ② , ③ . 其中正确的有( )
A、 B、 C、 D、11. 已知二次函数 ( 为常数, )当 时, ,则该函数图象的顶点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限12. 如图,是等边三角形,点D,E分别在 , 上,且 , , 与相交于点F,则下列结论:① , ② , ③ . 其中正确的有( ) A、3个 B、2个 C、1个 D、0个
A、3个 B、2个 C、1个 D、0个二、填空题
-
13. 因式分解: = .14. 如图,以BC为直径的圆与AC相切于点C,交AB于点D,若 , , 则tan∠ABC= .
 15. 如果a、b是一元二次方程x2-x-3=0的两个实数根,则多项式3b2+ab+3a的值为 .16. 如图, , AB=a,CD=b, . 则EF= .
15. 如果a、b是一元二次方程x2-x-3=0的两个实数根,则多项式3b2+ab+3a的值为 .16. 如图, , AB=a,CD=b, . 则EF= . 17. 用“●”“□”定义新运算:对于数a,b,都有a●b=a和a□b=b.例如3●2=3,3□2=2,则(2020□2021)●(2021□2020)= .18. 如图,在钝角三角形中, , , 点A、C关于轴对称,连接、 , 点P、Q分别是、上的动点,的最小值为 .
17. 用“●”“□”定义新运算:对于数a,b,都有a●b=a和a□b=b.例如3●2=3,3□2=2,则(2020□2021)●(2021□2020)= .18. 如图,在钝角三角形中, , , 点A、C关于轴对称,连接、 , 点P、Q分别是、上的动点,的最小值为 .
三、解答题
-
19. 计算: .20. 如图,已知在正方形ABCD中,M是AB的中点,E是AB延长线上一点,MN⊥DM且交∠CBE的平分线于N.试判定线段MD与MN的大小关系,并说明理由.
 21. 国家航天局消息:北京时间2022年12月4日,神舟十四号载人飞船返回舱在东风着陆场成功着陆,标志着神舟十四号载人飞行任务取得圆满成功,某中学科技兴趣小组为了解本校学生对航天科技的关注程度,在该校内进行了随机调查统计,将调查结果分为不关注、关注、比较关注、非常关注四类,回收、整理好全部调查问卷后,得到下列不完整的统计图:
21. 国家航天局消息:北京时间2022年12月4日,神舟十四号载人飞船返回舱在东风着陆场成功着陆,标志着神舟十四号载人飞行任务取得圆满成功,某中学科技兴趣小组为了解本校学生对航天科技的关注程度,在该校内进行了随机调查统计,将调查结果分为不关注、关注、比较关注、非常关注四类,回收、整理好全部调查问卷后,得到下列不完整的统计图: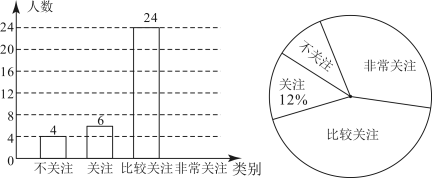 (1)、此次调查中接受调查的人数为人,扇形统计图中,“关注”对应扇形的圆心角为;(2)、补全图1条形统计图;(3)、该校共有900人,根据调查结果估计该校“关注”,“比较关注”及“非常关注”航天科技的人数共多少人?(4)、该校九年一班非常关注的学生有A、B、C、D四人,随机选取两人去参加学校即将举办的航天知识竞赛,请利用列表或画树状图的方法,求出恰好抽到A、B两位同学的概率.22. 一次函数y = x + b和反比例函数 (k≠0)交于点A(a,1)和点B.
(1)、此次调查中接受调查的人数为人,扇形统计图中,“关注”对应扇形的圆心角为;(2)、补全图1条形统计图;(3)、该校共有900人,根据调查结果估计该校“关注”,“比较关注”及“非常关注”航天科技的人数共多少人?(4)、该校九年一班非常关注的学生有A、B、C、D四人,随机选取两人去参加学校即将举办的航天知识竞赛,请利用列表或画树状图的方法,求出恰好抽到A、B两位同学的概率.22. 一次函数y = x + b和反比例函数 (k≠0)交于点A(a,1)和点B. (1)、求一次函数的解析式;(2)、求△AOB的面积;23. 锐角外接圆的圆心为O,线段的中点分别为M、N, , . 设 .
(1)、求一次函数的解析式;(2)、求△AOB的面积;23. 锐角外接圆的圆心为O,线段的中点分别为M、N, , . 设 .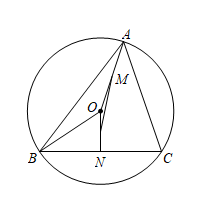 (1)、请直接用表示;(2)、判断的形状,并给出证明:(3)、求的大小.24. 已知:点P为图形M上任意一点,点Q为图形N上任意一点,若点P与点Q之间的距离PQ始终满足PQ>0,则称图形M与图形N相离.
(1)、请直接用表示;(2)、判断的形状,并给出证明:(3)、求的大小.24. 已知:点P为图形M上任意一点,点Q为图形N上任意一点,若点P与点Q之间的距离PQ始终满足PQ>0,则称图形M与图形N相离. (1)、已知点A(1,2)、B(0,-5)、C(2,-1)、D(3,4).
(1)、已知点A(1,2)、B(0,-5)、C(2,-1)、D(3,4).①与直线y=3x-5相离的点是 ;
②若直线y=3x+b与△ABC相离,求b的取值范围;
(2)、设直线y=x+3、直线y=-x+3及直线y=-2围成的图形为W,⊙T的半径为1,圆心T的坐标为(t,0),直接写出⊙T与图形W相离的t的取值范围.25. 如图,函数的图象经过点 , 两点,m,n分别是方程的两个实数根,且 . (1)、求m,n的值以及函数的解析式;(2)、设抛物线与x轴的另一个交点为C,抛物线的顶点为D,连接 , , , . 求证:;(3)、对于(1)中所求的函数 , 当时,求函数y的最大值和最小值.
(1)、求m,n的值以及函数的解析式;(2)、设抛物线与x轴的另一个交点为C,抛物线的顶点为D,连接 , , , . 求证:;(3)、对于(1)中所求的函数 , 当时,求函数y的最大值和最小值.